Потоки в сетях
Сетью
называется граф, элементам которого
поставлены в соответствие некоторые
параметры. Далее элементы множества R
будем называть узлами,
а множества
–
дугами.
Пусть каждой дуге
некоторой
сети
поставлено
в соответствие неотрицательное
(действительное) число
,
называемое пропускной
способностью дуги
.
Функция
,
отображающая множество
в
множество неотрицательных чисел,
называется функцией
пропускной способности.
Пусть s
и t
– два различных узла из R.
Стационарный поток
величины v
из s
в t
в сети
есть
функция f,
отображающая множество А
в множество неотрицательных чисел,
удовлетворяющая линейным уравнениям
и неравенствам
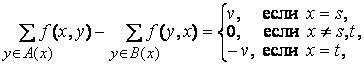(14.4)
(14.5)
где
(«после
x»),
(«перед
х»).
Будем называть узел s – источником, узел t – стоком, а остальные узлы – промежуточными.
Если
дан поток f,
то число
называется
дуговым
потоком
или
потоком
по дуге
.
Поскольку
и
удовлетворяют
условиям (14.4) и (14.5), вопрос о существовании
потока не возникает. Система уравнений
(14.4) избыточна, так как складывая все
строки ее матрицы, мы получаем нулевой
вектор. Таким образом, не нарушая
общности, можно отбросить одно из
уравнений системы.
Потоком
в сети
назовем
функцию f,
сопоставляющую каждому ребру
сети
целое число
и
обладающую следующими свойствами:
(кососимметрия),
(допустимость).