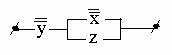8. Теорема Поста.

Система D = {f₁, f₂, ... f_m} булевых функций является полной тогда и только тогда, когда среди функций этой системы существуют: функция, не сохраняющая константу 0, функция, не сохраняющая константу 1, а также нелинейная, несамодвойственная и немонотонная функции.

Классы Поста:

Класс функций, сохраняющих ноль

Функция f(х₁, ..., х_n) называется сохраняющей ноль, если она на нулевом наборе принимает значение 0, то есть f(0, ..., 0) = 0.

Пример. f(х) = 0, f(х) = х, f(х₁, х₂) = х₁ • х₂, f(х₁, х₂) = х₁ Ú х₂ сохраняют ноль; f(х) = 1, f(х) =х, f(х₁, х₂) = х₁ ® х₂ не сохраняют ноль.

Класс функций, сохраняющих единицу

Функция f(х₁, ..., х_n) называется сохраняющей едини­цу, если она на единичном наборе принимает значение 1, то есть f (1, ..., 1) = 1.

Пример. Функции f(х) = 1, f(х) = х – сохраняют единицу; функции f(х) = 0, f(х) =х, f(х₁, х₂) = х₁ Å х₂ – не сохраняют единицу.

Класс самодвойственных функций

Функция f (х₁,..., х_n) называется самодвойственной, если f(х₁, ..., х_n) = f(х₁, ...,х_n).

Пример. f(х) = х, f(х) =х – самодвойствен­ные функ­ции; f(х₁, х₂) = х₁ • х₂, f(х₁, х₂) = х₁ Ú х₂ – несамо­двой­ственные.

Класс монотонных функций

Набор  = (₁, ..., _n) предшествует набору  = (₁, ..., _n), если _i  _i (i = l, 2, ..., n). Это обозначаем как   . Наборы, которые находятся в отношении  называются сравнимыми.

Функция f(х₁, ..., х_n) называется монотонной, если для любой пары наборов a и b таких, что при   : f()  f().

Пример. f(х) = х, f(х₁, х₂) = х₁ • х₂, f(х₁, х₂) = х₁ Ú х₂ – монотонные функции, а f(х) =х – немо­нотонная функция.

.

Класс линейных функций

Функция f(х₁, ..., х_n) называется линейной, если полином Жегалкина этой функции имеет линейный вид:

f(х₁, ..., х_n) = а₀ Å а₁ x₁ Å … Å а_n x_n,

где а_i  {0,1} (i = 0, l, ..., n).

Пример. f(х) = х, f(х) =х = х Å 1 – линейные функции; f(х₁, х₂) = х₁ Ú х₂ = х₁ Å х₂ Å х₁•х₂ – нелинейная функция.

Пример. Доказать полноту системы .

Решение. Пусть K₀ – класс функций, сохраняющих константу 0; К₁ – класс функций, сохраняющих константу 1; К_л, K_c, К_м – классы линейных, самодвойственных и монотонных функций соответственно.

Составим таблицу Поста следующего вида.

Таблица

№	φi	K0	К1	Кл	Kc	Км
1	X1 X2	+	–	+	–	–
2	X1  X2	+	+	–	–	+
3	1	–	+	+	–	–

Знак "+", стоящий на пересечении i- й строки и j-гo столбца этой таблицы, показывает, что функция φ_i – принадлежит соответствующему классу, записанному в j-ом столбце,

Из табл. 1 видим, что φ₁ = f₇ не сохраняет константу 1 и не является монотонной, φ₂ = f₈ – нелинейная и несамодвойственная функция, φ₃ = f₁₆ не сохраняет константу 0. Следовательно, все условия теоремы Поста выполнены, и заданная система является полной.

9. РКС

Релейно-контактная схема представляет собой устройство из проводников и контактов, связывающих полюса источника тока. Контакты могут быть размыкающими и замыкающими. Каждый контакт подключен к некоторому реле. Когда реле находится под током, все подключенные к нему замыкающие контакты замкнуты, а размыкающие - разомкнуты.

         Каждому реле можно поставить в соответствие значение 1, если оно находится под током, и 0, если нет. Все замыкающие контакты, подключенные к реле х, будем обозначать x₁, ... x_n, а размыкающие - .

         Всей схеме также можно поставить одно из двух значений 1, если схема проводит ток, и 0, если не проводит. Это значение есть функция переменных х_i, , т.е. логическая функция. Эту функцию называют функцией проводимости электрической цепи.

         Всякая формула алгебры высказываний может быть реализована некоторой релейно-контактной схемой, имеющей соответствующую функцию проводимости. И наоборот, для некоторой схемы можно указать ее функцию проводимости, логическую функцию, а затем построить для нее некоторую формулу алгебры высказываний. При этом основные логические связки моделируются следующими элементарными схемами:

 

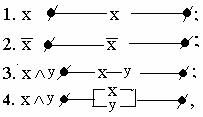
т.е. дизъюнкция моделируется параллельным соединением проводников, конъюнкция - последовательным.

Пример: Построить наиболее простую релейно-контактную схему по заданной функции проводимости f(x,y,z): f(0,1,0)=f(1,1,0)=f(1,1,1)=0.

         Строим СКНФ: , т.к. эти сомножители обращаются в "0" на указанных наборах функции: (0,1,0), (1,1,0), (1,1,1).

         Далее упрощаем формулу S: