
- •28. Виды и способы отбора единиц в выборочной совокупности.
- •29.Простая (случайная) и Механическая выборка
- •30.Типическая и серийная выборки.
- •31.Малая выборка
- •32. Парный и многофакторный корреляционный анализ.
- •33. Оценка тесноты связи…..(из лекции, не моей, поэтому че да как не знаю((, долго мучился с этим вопросом)
- •34. Ряды динамики: понятие, виды, задачи.
- •35. Аналитические показатели рядов динамики.
34. Ряды динамики: понятие, виды, задачи.
Ряд динамики - это последовательность числовых значений изучаемого показателя, расположенных в хронологическом порядке. Числовые значения показателя, составляющие динамический ряд, называется уровнями ряда. Уровни динамического ряда могут относиться к отдельным моментам или интервалу времени. В зависимости от этого различают моментные и интервальные ряды динамики.
Моментным называется ряд, уровни которого характеризуют величину изучаемого показателя по состоянию на определенные моменты времени.
Интервальным называется ряд, уровни которого характеризуют величину показателя за определенные периоды времени.
Кроме того, ряды динамики подразделяют на ряды абсолютных, относительных и средних величин. Ряды динамики абсолютных величин рассматриваются как исходные, а ряды относительных и средних величин - как производные от них. При изучении динамики социально-экономических явлений чаще используют производные интервальные ряды.
35. Аналитические показатели рядов динамики.
При изучении рядов динамики определяют направление и скорость изменения его уровней. С этой целью рассчитывают такие показатели, как абсолютные приросты, темпы роста и прироста. Для иллюстрации расчета показателей будем рассматривать динамический ряд из n-уровней: у1,у2,…,уn.
Темпы роста показывают во сколько
раз некоторый уровень больше или меньше
другого уровня ряда, т.е. характеризует
интенсивность изменения уровней ряда.
Если каждый уровень сопоставляется с
предыдущим уровнем ряда, то получают
цепные темпы роста
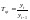 ,t=2;…;n.
Если все уровни ряда сопоставимы с одним
и тем же уровнем, принятым за базу
сравнения, то получают базисные темпы
роста
,t=2;…;n.
Если все уровни ряда сопоставимы с одним
и тем же уровнем, принятым за базу
сравнения, то получают базисные темпы
роста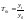 .
.
Между цепными и базисными темпами роста
существует взаимосвязь, позволяющая в
случае необходимости переходить от
одного к другим. Например, произведение
цепных темпов роста дает базисные темпы
роста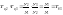 .
Результат деления двух базисных темпов
роста равен цепному темпу
.
Результат деления двух базисных темпов
роста равен цепному темпу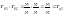 .
.
Абсолютный прирост характеризует
абсолютную скорость изменения уровней
ряда. Он показывает, на сколько единиц
измерения некоторый уровень больше или
меньше другого уровня ряда. Абсолютные
приросты могут рассчитываться как
цепные
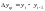 или
как базисные
или
как базисные
 .
.
Темп прироста показывает на сколько
% некоторый уровень больше или меньше
другого уровня ряда, он характеризует
абсолютное изменение темпа роста и
рассчитывается по формуле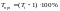 ,
,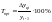 ,
, .
.
Разделив абсолютный прирост на темп
прироста за соответствующий период,
получим показатель абсолютного значения
1% прироста .
Абсолютное значение 1% прироста = 0,01
предыдущего уровня ряда. Для базисных
абсолютных приростов и темпов прироста
расчет этого показателя не имеет смысла,
т.к. будет получаться одно и то же число.
.
Абсолютное значение 1% прироста = 0,01
предыдущего уровня ряда. Для базисных
абсолютных приростов и темпов прироста
расчет этого показателя не имеет смысла,
т.к. будет получаться одно и то же число.
