17. Конусные предохранительные муфты
Конусные предохранительные муфты отличаются хорошей расцепляемостью, однако имеют значительные радиальные раз-меры и отличаются высокими требованиями к соосности соединяемых валов и точности изготовления рабочих поверхностей (рис. 17.1). На точность срабатывания этих муфт влияют давление; шероховатость трущихся поверхностей; закон изменения нагрузки на муфту; продолжительность неподвижного контакта фрикционных поверхностей; нагрузка на муфту перед перегрузкой. Существенное влияние на точность срабатывания муфты оказывает шероховатость трущихся поверхностей: чем чище поверхность, тем сильнее сказывается влияние перечисленных выше факторов, поэтому не следует устанавливать слишком высокое значение параметра шероховато-сти трущихся поверхностей.
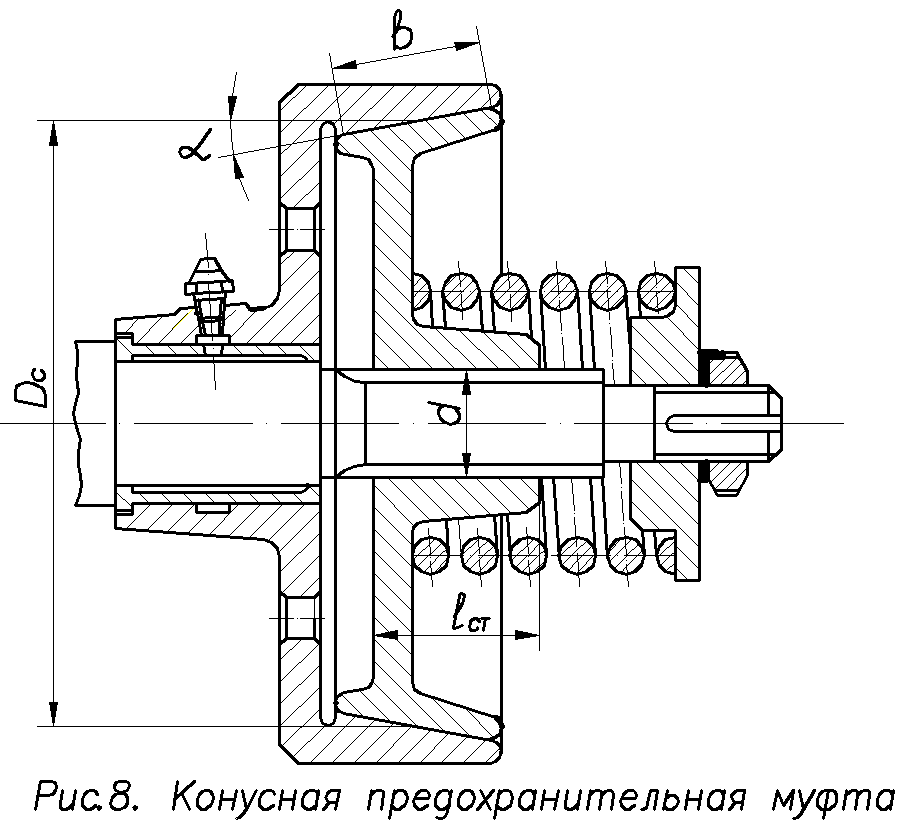
Рис. 17.1. Конусная предохранительная муфта
При конструировании и изготовлении муфт для соединения валов надо обеспечивать строгую соосность валов, равномерный контакт трущихся поверхностей, предусматривая с этой целью приработку конусов. Материал полумуфт – чугун СЧ 15-32, СЧ 21-404, для трущихся поверхностей – сочетания чугун по чугуну, по стали, по бронзе – допускается применение асбестовых обкладок и металлокерамических покрытий.
Конусность назначают
с тем расчётом, чтобы угол α был значительно
больше угла трения, практически принимают
.
Конусные муфты могут работать как со
смазкой трущихся поверхностей, так и
без нее.
18. Расчет конусной предохранительной муфты, обеспечивающей передачу крутящего момента
Исходные данные:
Т = 100 Нм при коэффициенте перегрузки = 1,5, диаметре вала ведомой полумуфты d = 28 мм.
1.
Для ведомой полумуфты назначаем материал
чугун, а для
сопряженной – сталь закаленную. Для
выбранных материалов при работе
без смазки
коэффициент трения контактирующих
поверхностей полумуфт f
= 0,1…0,15; допускаемое давление
= (1…1,2 МПа ([12, с. 477])).
Угол
во избежание заклинивания муфты должен
быть больше угла трения
;
для чугунных муфт принимают
.
Назначаем
= 10°.
Отношение ширины b контактирующих поверхностей к сред-нему диаметру Dc принимают в пределах
Назначаем
=
0,25.
2. Критерием работоспособности муфты служит величина среднего давления p:
.
Здесь Fn – нормальная сила, сжимающая поверхности трения полумуфт;
,
где Q1 – сила нажатия пружины.
Под действием силы Q1 на поверхностях контакта возникает сила трения, достаточная для передачи окружного усилия Ft:
Тогда
b = 156 0.25 = 39 мм. Принимаем b = 40 мм.
3. Усилие для включения муфты
4. Усилие, необходимое для удержания муфты во включенном состоянии:
5. Определяем конструктивно размеры диаметра dст, длины lст, ступиц:
18.1. Расчет пружины
1. Задаемся материалом пружины и выбираем величину допускаемого напряжения.
Материал – стальная
углеродистая проволока II
класса (выносливость в циклах не менее
1
циклов), 3-го разряда из стали 65С2ВА
([12, с. 488…489]); допускаемое напряжение
= 750 МПa.
2. Диаметр проволоки
Назначаем индекс
пружины
3. Определяем коэффициент, учитывающий кривизну витков:
При
этом средний диаметр у пружины
= 6
11,5 = 69 мм;
наружный диаметр
= 69 + 11,5 = 80,5 мм;
внутренний диаметр
= 69 – 11,5 = 57,5
мм.
Внутренний диаметр
4. Изменение высоты (осадку) цилиндрической винтовой пру-жины из проволоки круглого сечения определяют по формуле
где n – число рабочих витков пружины,
G = 8 104 МПа – модуль сдвига для стали.
Изменение высоты прямо пропорционально нагрузке. При известных значениях Q2, С, G, d значением F2 либо n нужно задаваться, исходя из условий работы, габаритов муфты, если неизвестен график зависимости F2 от Q2, так называемая характеристика пружины.
В данном случае, принимая n = 4, получаем
5. Полное число витков пружины
.
6. Высота H3 при посадке витка на виток
7. Зазор между витками пружины в ненагруженном состоянии
8. Шаг пружины в свободном состоянии
9. Высота пружины H0 в свободном состоянии
10. Длина l заготовки проволоки для пружины
11. Высота пружины H2 при действии силы Q2.
