Проверка передачи на выносливость при изгибе

Проверочный расчет на усталость по напряжениям изгиба выполняем по условию прочности ([6], cтр. 339) σ_F ≤ σ_FР.

Расчетное местное напряжение при изгибе определяем по формуле, [ ]

_{σF = КF  YFS  Yβ  Yε  Ft / (0,85  bw  m).}

Коэффициентов нагрузки К_F вычисляют следующим образом, [ ]:

_{КF = КА  КF  КFβ  КFα,}

где К_А – коэффициент, учитывающий внешнюю динамическую нагрузку; К_А = 1;

– коэффициент, учитывающий динамическую нагрузку, возникающую в зацеплении ([ ], cтр. )

ω_{F v} · b_w

К _{F v} = 1+ ———— ,

F_t · К_А

где ω_{F v} - удельная окружная динамическая сила, Н/мм

ω_{F v} = δ_F · g₀ · v ,

δ_F - коэффициент, учитывающий влияние вида зубчатой передачи и модификации профиля головок зубьев (см. табл. 5.6 и [6], стр. 329, табл. 18.2), δ_F = 0,016;

g_{0 -} коэффициент, учитывающий влияние разности шагов зацепления зубьев шестерни и колеса (см. табл. 5.7 и [6], стр. 329, табл. 18.3), g₀ = 5,6;

ω_{F v} = 0,016 · 5,6 · 3,03 = 2,433 Н/мм ,

2,433 · 34

К _{F v} = 1+ ———— = 1,069;

1193 · 1

К_Fβ – коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий; так как , следовательно К_{F β} = 1,21 (см. рис. 6.3, cтр. );

К_Fα – коэффициент, учитывающий распределение нагрузки между зубьями, для прямозубых передач К_Fα = 1.

_{КF = 1 · 1,069 · 1,21 · 1 = 1,293;}

Y_FS – коэффициент, учитывающий форму зуба и концентрацию напряжений; принимается в зависимости от эквивалентного числа зубьев z_ и коэффициента смещения инструмента X ([ ] , cтр. , рис. );

z_1 = z₁ / сosδ₁; z_2 = z₂ / сosδ₂;

z_1= 19 / cos17,57˚ = 19,93; Y_FS1 = 4,08;

z_2 = 60 / cos 72,429˚ = 198,75; Y_FS2 = 3,6.

Расчет выполняется для менее прочного зубчатого колеса, т.е. для того из колес, у которого отношение σ_FP / Y_FS меньше;

шестерня: σ_FP1 / Y_FS1 = 370,59 / 4,08 = 90,83 Мпа.

колесо: σ_FP2 / Y_FS2 = 345,88 / 3,6 = 96,08 МПа.

Расчет ведем по шестерне.

Y_β – коэффициент, учитывающий наклон зуба; для прямозубых колес Y_β = 1;

Y_ε – коэффициент, учитывающий перекрытие зубьев; для прямозубых колес Y_ε = 1.

_{F 1 = 1,293 · 4,08 · 1 · 1 · 1149,05 / (0,85 · 34 · 3,21) = 65,34 МПa;}

_{65,34<370,59 – условие прочности выполняется.}

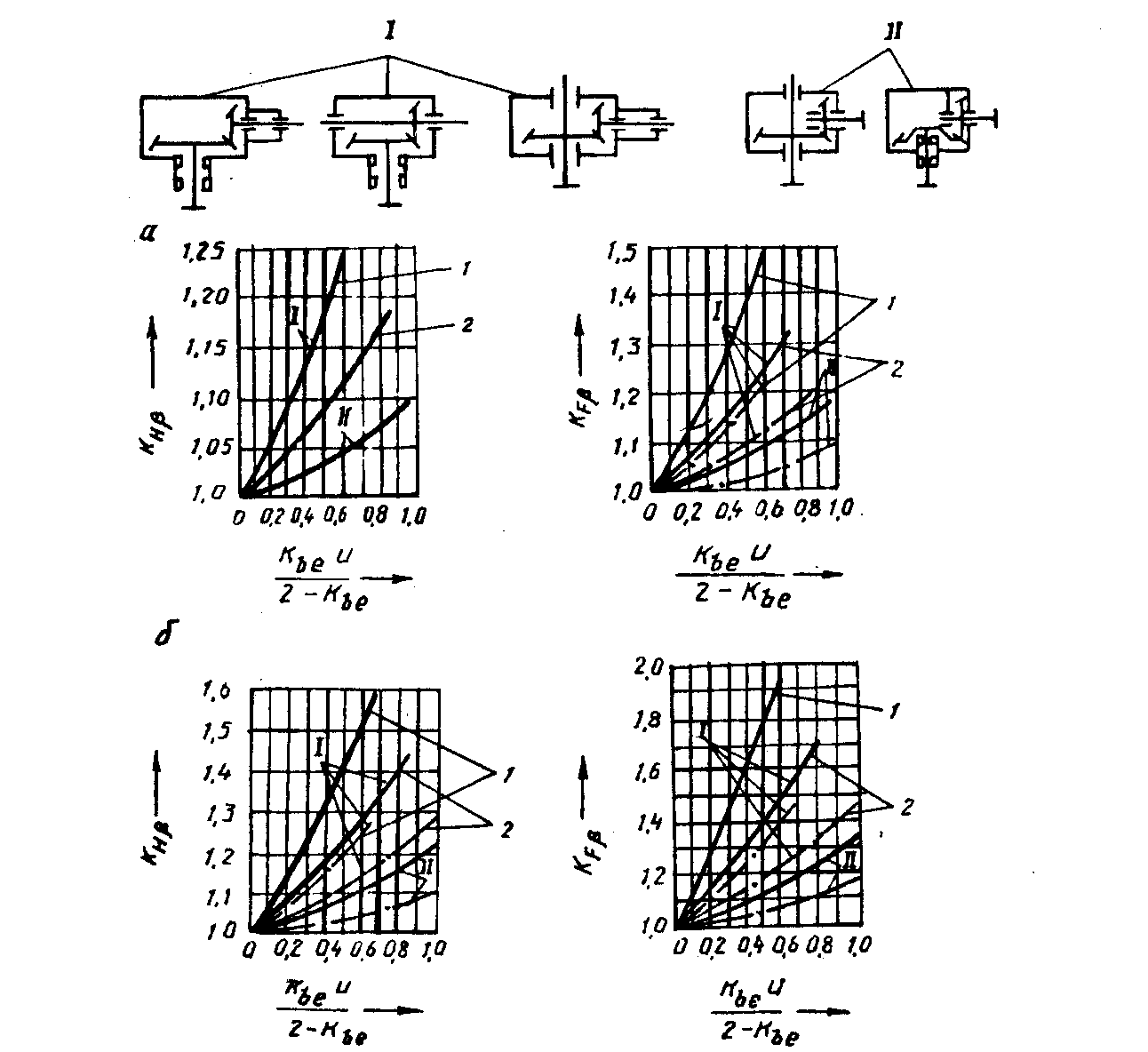
Рис. 6.3. Графики для определения К_нβ и К_Fβ для конических зубчатых колес:

а – при твердости рабочих поверхностей зубьев H₁ ≤ 350 НВ; Н₂ ≤ 350 НВ (или H₁ > 350 НВ; Н₂ < 350 НВ); б – при H₁ > 350 НВ; Н₂ > 350 НВ; I, II – кривые,

соответствующие виду передачи (см. верхнюю часть рисунка); 1 – для передач

с опорами на шариковых подшипниках; 2 – то же, на роликовых подшипниках;

 для колес с прямыми зубьями;  ·  для колес с круговыми зубьями [8, cтр. 189]

[6, стр. 338; 8, стр. 190].

7. Расчет привода с червячным редуктором

и цепной передачей

П одобрать электродвигатель, выполнить кинематический и силовой расчет привода, расчет червячной и цепной передач (см. рис. 7.1).

Рис. 7.1. Схема привода

Исходные данные

1. Мощность на валу ведомой звездочки цепной передачи Р_з = = 4,0 кВт.

2. Частота вращения вала ведомой звездочки n_з = 48 мин^-1.

3. Общее передаточное число привода U_общ = 60.

4. Нагрузка постоянная.

5. Выпуск серийный.

6. Требуемая долговечность привода L_n = 15000 ч.

7.1. Выбор электродвигателя, кинематический и силовой

расчет привода

Общий КПД привода (см. таблицу 3.1):

_общ = ₁  ₂  ₃  (₄)³ = 0,98  0,8  0,95  (0,995)³ = 0,734;

где ₁ = 0,98 – КПД муфты;

₂ = 0,8 – КПД червячной передачи при предварительных расчетах;

₃ = 0,95 – КПД открытой цепной передачи;

₄ = 0,995 – КПД пары подшипников качения.

Определяем требуемую мощность и частоту вращения вала электродвигателя.

P_тр = P_з / _общ = 4,0 / 0,734 = 5,45 кВт;

n_тр = n_з  U_общ =48  60 = 2880 мин^-1.

Выбираем асинхронный электродвигатель 4А100L2 с номинальной мощностью Р = 5,5 кВт, синхронной частотой вращения n_cинхр = 3000 мин^-1, асинхроннной частотой вращения n_асинхр = 2880 мин^-1 (см таблицу 3.3).

Распределяем общее передаточное число привода между передачами. Принимаем передаточное число червячной передачи U_чп = 20, цепной передачи – U_цп = U_общ / U_чп = 60 / 20 = 3.

Выполняем кинематический расчет привода.

Мощности на валах:

P₁ = P_потр  ₁  ₄ = 5,45  0,98  0,995 = 5,314 кВт;

P₂ = P₁  ₂  ₄ = 5,314  0,8  0,995 = 4,23 кВт;

P₃ = P₂  ₃  ₄ = 4,23  0,95  0,995 = 4 кВт.

Частота вращения валов:

n₁ = n_ас.дв = 2880 мин^-1;

n₂ = n₁ / U_чп = 2880 / 20 = 144 мин^-1;

n₃ = n₂ / U_цп = 144 / 3 = 48 мин^-1.

Крутящие моменты:

Т₁ = 9,55  10³  Р₁ / n₁ = 9550  5,314 / 2880 = 17,621 Н  м;

Т₂ = 9,55  10³  Р₂ / n₂ = 9550  4,23 / 144 = 280,53 Н  м;

Т₃ = 9,55  10³  Р₃ / n₃ = 9550  4 / 48 = 795,83 Н  м