6.2. 3. Определение геометрических параметров передачи и колес

При проектировочном расчете передач с колесами, имеющими твердость Н_HB ≤ 350 НВ рекомендуется первоначально из условия контактной прочности вычислять внешний делительный диаметр колеса d _е2, [ ]:

d_е2 = K_{d ,}

где K_d – вспомогательный коэффициент, учитывающий тип передачи; K_d = 99 - для прямозубых передач, K_d = 86 - для косозубых передач, [ ];

К_Нβ – коэффициент, учитывающий неравномерность распределения нагрузки по ширине зубчатого венца, принимают по графику ([ ] cтр. , рис. ) в зависимости от отношения

К_bе U / (2 - К_bе),

где К_bе - коэффициент ширины зубчатого венца b относительно внешнего конусного расстояния R_e; рекомендуется К_bе = 0,2…0,3;

ψ _bRe = – коэффициент длины зуба, при проектировании редукторов со стандартными параметрами принимается ψ _bRe = 0,285,[ ].

Так как ,

К_Нβ = 1,2 ([ ]. , cтр. , рис. ).

d_е2 = 99 ₌ 211,61 мм.

Полученную величину округляем до номинального значения внешнего делительного диаметра колеса по ГОСТ 12289 – 76 ([ ], cтр. 49) d_е2 = 225 мм. По ГОСТ 12289 – 76 принимаем также рабочую ширину зацепления b_w = 34 мм. В дальнейших расчетах следует учитывать требования ГОСТ по выполнению следующих условий: b_w≤0,3 R_{e ,} b_w≤ 10m_e.

Согласно рекомендаций [ ], число зубьев конической шестерни Z₁ = 18…32.

Принимаем Z₁ = 19, тогда Z₂ = u Z₁ = 3,15  19 = 59,85. Принимаем Z ₂ = 60.

Фактическое передаточное число передачи

u_ф = Z ₂ / Z₁ = 60 / 19 = 3,158.

Δu = (u - u_ф) / u · 100% = (3,158 – 3,15 ) / 3,15 · 100% = 2,5% , что допустимо.

Внешний окружной модуль

m _e = d _e2 / Z₂ = 225 / 60 = 3,75 мм.

Внешний делительный диаметр шестерни

d _e1 = d _е2 / u = 225 / 3,158 = 71,25 мм.

Определим углы делительных конусов, [ ]

tgδ₂ = u = 3,158; δ₂ = arctg 3,158 = 72,429 ⁰ = 72˚ 25΄ 45^'';

δ₁ = 90 - δ₂; δ₁ = 90˚ - 72 ˚25΄ 45^'' = 17,57˚^'= 17˚34΄15^''.

_{Внешнее конусное расстояние:}

_{Re = ; Re мм.}

Среднее конусное расстояние:

R = R_e – 0,5  b = 118,014 – 0,5  34 = 101,014 мм.

Средний окружной модуль:

m = m _e · R / R_e = 3,75 · 101,014 / 118,014 = 3,21 мм.

Средний делительный диаметр:

d ₁ = d _е1 – b · sin δ₁ = m · Z₁ = 3,21 · 19 = 60,99 мм;

d ₂ = m · Z₂ = 3,21 · 60 = 192,6 мм.

Коэффициент смещения:

x₁ = = 0,412;

где β_m = 0, так как передача прямозубая;

x₂ = - x₁ = - 0,412.

Коэффициент расчетной толщины зуба исходного контура:

x_τ1 = 0,03 + 0,008(u – 2,5) = 0,03 + 0,008(3,158 – 2,5) = 0,035;

x_τ2 = - x_τ1 = -0,035.

Внешняя высота головки зуба:

h _{a e1} = ( 1 + x₁ ) m _e = ( 1 + 0,412 ) 3,75 = 5,295 мм;

h _{a e2} = ( 1 + x₂ ) m _e = ( 1 - 0,412 ) 3,75 = 2,205 мм.

Внешняя высота ножки зуба:

h _fe1 = h _{a e2} + 0,2 · m _e = 2,205 + 0,2 · 3,75 = 2,955 мм;

h _fe2 = h _{a e1} + 0,2 · m _e = 5,295 + 0,2 · 3,75 = 6,045 мм.

Внешняя высота зуба:

h_e1 = h _{a e1} + h _fe1 = 5,295 + 2,955 = 8,25 мм;

h_e2 = h _{a e2} + h _fe2 = 2,205 + 6,045 = 8,25 мм.

Внешняя окружная толщина зуба:

S_e1 = (0,5π + 2 x₁tgα + x_τ1) m _e =

= (0,5π + 2·0,412·tg20⁰+0,035)3,75 = 7,14 мм;

S_e2 = π m _e - S_e1 = π·3,75 – 7,14 = 4,64 мм.

Угол ножки зуба:

θ _f1 = arctg (h _fe1/ R_e) = arctg (2,955 /118,014) =

= 1,4344 ⁰ = 1˚26΄4^'';

θ _f2 = arctg (h _fe2 / R_e) = arctg (6,045 / 118,014) =

= 2,9323 ⁰ = 2˚55΄56^''.

Угол головки зуба:

θ _a1 = θ _{f 2} = 2˚55΄56^''; θ _a2 = θ _{f 1} =1˚26΄4^'' .

Угол конуса вершин:

δ _а1 = δ₁ + θ _a1 = 17˚34΄15^'' + 2˚55΄56^'' = 20˚30΄11^'';

δ _а2 = δ₂ + θ _a2 = 72˚25΄45^'' + 1˚26΄4^'' = 73˚51΄49^''.

Угол конуса впадин:

δ _f1 = δ₁ - θ _f1 = 17˚34΄15^'' - 1˚26΄4^'' = 16˚8΄11^'';

δ _f2 = δ₂ - θ _f2 = 72˚25΄45^'' - 2˚55΄56^'' = 69˚ 29΄ 49^''.

Внешний диаметр вершин зубьев:

d _ae1 =d _е1 + 2· h _{a e1} · cos δ₁ = 71,25 + 2 · 5,295 · cos 17˚34΄15^'' = 81,346 мм;

d _ae2 =d _е2 + 2· h _{a e2} · cos δ₂ = 225 + 2 · 2,205 · cos 72˚25΄45^'' = 226,33 мм.

Проверим коэффициенты ширины венца

ψ _bRe = = 34 / 118,014 = 0,288 < 0,3;

ψ_bd = b_w / d ₁ = 34 / 60,99 = 0,557.

Условия выполняются.

Средняя окружная скорость зубчатых колес:

v = π · d ₁ · n ₁ / 60 = 3,14 · 60,99 · 10^-3 · 950 / 60 = 3,03 м/с.

Принимаем 8 – ю степень точности изготовления зубчатых колес (см. табл. 5.6, стр. 51).

Определяем значения усилий в коническом зацеплении:

- окружная сила на шестерне и колесе

F_t1 = F_{t 2} = 2 · Т₂ / d_wm2 = 2·113110/ 196,875 =1149,05 Н;

d_wm2 = 0,857 d_е2 = 0,857·225 = 196,875 мм.

- радиальная сила на шестерне, численно равная осевой силе на колесе

F_r1 = F_а2 = F_t · tg α · cos δ₁ = 1149,05· tg 20 ⁰ · cos 17˚34΄15^'' = 393,14 Н;

- осевая сила на шестерне, численно равная радиальной силе на колесе

F_а1 = F_r2 =F_t · tg α · sin δ₁ = 1149,05· tg 20 ⁰ · sin 17˚34΄15^'' = 125,76 Н,

где d_wm – средний начальный диаметр; α – угол профиля исходного контура; δ – угол делительного конуса.

Изобразим схему действия сил (рис. 6.2.).

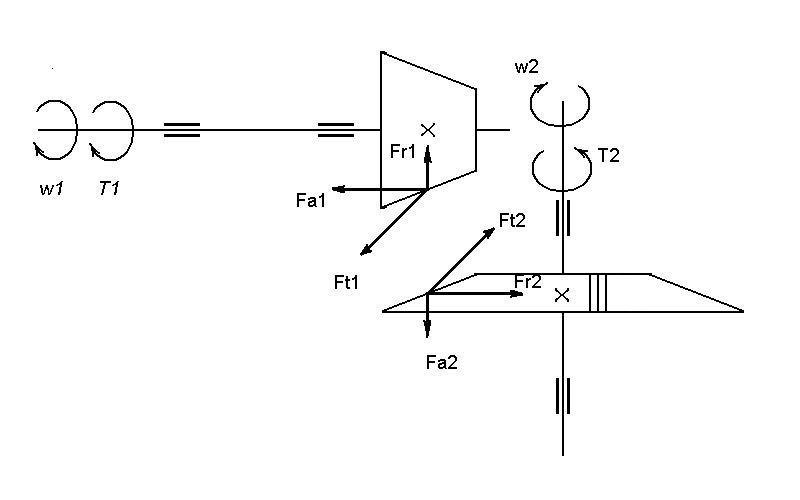
Рис. 6.2. Схема действия сил в прямозубом коническом

зацеплении

Произведем проверку передачи по контактным напряжениям

Проверочный расчет передачи на контактную усталость активных поверхностей зубьев выполняем по условию контактной прочности, [ ]

_{σH = zЕ  zH  zε ,}

где z_Е – коэффициент, учитывающий механические свойства сопряженных зубчатых колес; для стальных зубчатых колес z_E =192 МПа^1/2 , [ ];

z_H – коэффициент, учитывающий форму сопряженных поверхностей зубьев в полюсе зацепления, [ ]:

z_H = ;

где α_w = 20⁰ – угол зацепления

_{zH = ;}

z_ε – коэффициент, учитывающий суммарную длину контактных линий, для прямозубых колес z_ε = 1 ([ ], cтр. )

K_Hβ = 1,0 (см. ранее).

К_Н – коэффициент, учитывающий динамическую нагрузку, возникающую в зацеплении ([ ], стр. );

ω_Hv · b_w

К _Hv = 1+ ———— ,

F_t · К_А

где ω_Hv - удельная окружная динамическая сила, Н/мм ([6], стр. 328);

К_А – коэффициент, учитывающий внешнюю динамическую нагрузку; К_А = 1 ([6], cтр. 329);

ω_Hv = δ_Н · g₀ · v ,

δ_Н - коэффициент, учитывающий влияние вида зубчатой передачи и модификации профиля головок зубьев (см. табл. 5.6 и [6], стр. 329, табл. 18.2), δ_Н = 0,06;

g_{0 -} коэффициент, учитывающий влияние разности шагов зацепления зубьев шестерни и колеса (см. табл. 5.7 и [6], стр. 329, табл. 18.3), g₀ = 5,6 ;

ω_Hv = 0,06 · 5,6 · 3,03 = 9,123 Н/мм ;

9,12 · 34

К _Hv = 1+ ———— = 1,27;

1149,0 5 · 1

_{σH = 192  2,495 486,35 МПа.}

Определяем процент перегрузки

По принятым в машиностроении нормам для σ_H допускается отклонение + 5% (перегрузка) и – 10% (недогрузка). Условие прочности выполняется.