Огляд літератури

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный университет Львовская политехника

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

ПОП_Сем.docx

Скачиваний:

Добавлен:

01.04.2025

Размер:

339.14 Кб

Скачать

☆

1 / 41 2 3 4 > Следующая >>>

МІНІСТЕРСТВО ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ

НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ «ЛЬВІВСЬКА ПОЛІТЕХНІКА»

КАФЕДРА АВТОМАТИЗОВАНІ СИСТЕМИ УПРАВЛІННЯ

Розрахункова робота №1 та №2

з дисципліни «Проблемно-орієнтоване програмування»

на тему

Пошук шляхів у неорієнтованому графі

Виконав:

студент гр. КН-22

Семенюк Олександр

Прийняв:

Доцент кафедри АСУ

Шпак З. Я.

Львів 2013

Зміст стор.

Вступ ………………………………………………………………………3

1. Огляд літератури ……………………………………………….………6

2. Формулювання задачі ………………………………………………….7

3. Алгоритм розв’язання задачі …………………………………...……..8

3.1. Загальний опис алгоритму ……………………………………8

3.2. Укрупнена блок-схема алгоритму ……………………………9

3.3 Блок-схеми підпрограм ………………………………..………10

4. Програмна реалізація алгоритму ……………………………………..16

4.1. Загальна характеристика та призначення програми..……….16

4.3. Вхідна та вихідна інформація ………………………………..16

4.4. Таблиця ідентифікаторів .……………………………………17

4.5. Структура програми та опис функцій ………………………18

5. Інструкція користувачеві програми …………………………………..19

6. Контрольні приклади та результати їх реалізації ……………………20

Висновки …………………………………………………………………..21

Список літератури ………………………………………………………...22

Додатки …………………………………………………………………….24

Додаток 1. Тексти програмних файлів ……………………………24

Додаток 2. Роздруки вхідних та відформатованих файлів контрольних прикладів ……………………………………………….28

Вступ

Г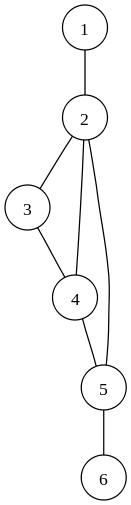 раф — це сукупність об'єктів із зв'язками між ними.

Об'єкти розглядаються як вершини, або вузли графу, а зв'язки — як дуги, або ребра. Для різних областей використання види графів можуть відрізнятися орієнтовністю, обмеженнями на кількість зв'язків і додатковими даними про вершини або ребра.

Велика кількість структур, які мають практичну цінність в математиці та інформатиці, можуть бути представлені графами. Наприклад, будову Вікіпедії можна змоделювати за допомогою орієнтованого графу, в якому вершини — це статті, а дуги (орієнтовані ребра) — посилання на інші статті.

Першою працею з теорії графів як математичної дисципліни вважають статтю Леонарда Ейлера (1736), у якій розглядалася задача про Кенігсбергські мости. Наступний імпульс теорія графів отримала близько 100 років потому з розвитком досліджень по електричним мережам, кристалографії, органічній хімії та іншим наукам.

Граф або неорієнтований граф G — це впорядкована пара G:=(V,E), для якої виконуються наступні умови:

— множина вершин або вузлів,

— множина пар (у випадку неорієнтованого графу — невпорядкованих) вершин, які називають ребрами.

(і так само ) зазвичай вважаються скінченними множинами. Велика кількість результатів, отриманих для скінченних графів, невірна (або інша) для нескінченних графів. Це пов'язано з тим, що певний набір ідей стає хибним у випадку нескінченних множин.

Орієнтований граф

Граф, який містить тільки ребра називається неорієнтованим, який містить тільки дуги — орієнтованим. Граф, що має як ребра так і дуги, називається мішаним. Якщо пара вершин сполучається кількома ребрами чи дугами одного напрямку, то ребра (дуги) називають кратними (паралельними). Дуга чи ребро що сполучає вершину саму із собою називається петлею. Граф без кратних дуг і петель називається простим.

Вершини сполучені ребром чи дугою називають суміжними, також називають суміжними ребра, що мають спільну вершину. Ребро (чи дуга) і її вершина називаються інцидентними. Ребро (u, v) з'єднує вершини u і v, дуга (u, v) починається у вершині u і закінчується у вершині v.

Кожен граф можна відобразити в евклідовому просторі множиною точок, які відповідають вершинам, сполучених лініями, що відповідають ребрам (дугам).

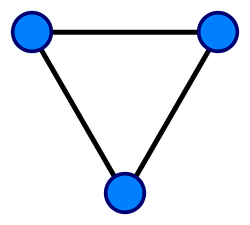
П овний граф — простий граф, в якому кожна пара різних вершин суміжна, тобто існує ребро, що сполучає ці вершини. Повний граф зазвичай позначається Kn.

Повний граф з n вершинами має n(n - 1)/ 2 ребер

Способи завдання графів

Графи можна задавати також за допомогою матриць. Занумеруємо всі вершини графа G натуральними числами від 1 до n. Матрицею суміжності A графа G називається квадратна nn-матриця, в якій елемент a_ij i-го рядка і j-го стовпчика дорівнює 1, якщо вершини v_i та v_j з номерами i та j суміжні, і дорівнює 0 у противному разі.

Приклад 3.3. Для графів G₁ i G₂ маємо відповідно

A₁=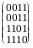 i A₂=

Очевидно, що матриці суміжності графів  симетричні.

Занумеруємо всі вершини графа G числами від 1 до n і всі його ребра  числами від 1 до m. Матрицею інцидентності B графа G називається nm-матриця, в якій елемент b_ij i-го рядка і j-го стовпчика дорівнює 1, якщо вершина v_i з номером i інцидентна ребру e_j з номером j, і дорівнює 0 у противному разі.

Приклад 3.4. Для графів G₁ і G₂маємо (ребра графів нумеруємо в тому порядку, в якому вони виписані в прикладі 3.1)

B₁=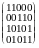 і B₂=

Нарешті, ще одним способом завдання графів є списки суміжності. Кожній вершині графа відповідає свій список. У список, що відповідає вершині v, послідовно записуються всі суміжні їй вершини.

Приклад 3.5. Для графів G₁ і G₂ маємо списки

G₁: G₂:

v₁: v₃,v₄ v₁: v₂,v₄,v₅

v₂: v₃,v₄ v₂: v₁,v₃,v₄

v₃: v₁,v₂,v₄ v₃: v₂,v₅

v₄: v₁,v₂,v₃ v₄: v₁,v₂,v₅

v₅: v₁,v₃,v₄

Вибір та зручність того чи іншого зі способів завдання графів залежать від особливостей задачі, яка розв’язується.

Огляд літератури

Оре О. Теорія графів. М.: Наука, 1968. 336с. http://eqworld.ipmnet.ru/ru/library/books/Ore1965ru.djvu
Уілсон Р. Введення в теорію графів. Пер з англ. М.: Мир, 1977. 208с. http://eqworld.ipmnet.ru/ru/library/books/Uilson1977ru.djvu
Харарі Ф. Теорія графів. М.: Мир, 1973. http://eqworld.ipmnet.ru/ru/library/books/Harari1973ru.djvu
Кормен Т. М.І ін Частина VI. Алгоритми для роботи з графами / / Алгоритми: побудова й аналіз = INTRODUCTION TO ALGORITHMS - 2-е вид. - М .: "Вільямс", 2006. - С. 1296. - ISBN 0-07-013151-1.
Салій В. Н. Богомолов А. М. Алгебраїчні основи теорії дискретних систем - М .: Фізико-математична література, 1997. - ISBN 5-02-015033-9.
Емелічев В. А., Мельников О. І., Сарванов В. І., Тишкевич Р. І. Лекції з теорії графів. М.: Наука, 1990. 384с. (Ізд.2, испр. М.: УРСС, 2009. 392 с.)
Кірсанов М. Н. Графи в Maple. М.: Физматлит, 2007. – 168
Повний граф [Eлектронний ресурс]. – Режим доступу : http://uk.wikipedia.org/wiki/Повний _граф
Граф (математика) [Eлектронний ресурс]. – Режим доступу : http://uk.wikipedia.org/wiki/Граф (математика)

Формулювання задачі

У даному завданні потрібно знайти усі шляхи від першої вершино до останньої. Підчас руху ми не повинні попадати в одну вершину двічі.

Вихідними даними буде список вершин по яких було пройдено в результаті руху від першої до останньої вершин включно.

Алгоритм розв’язання задачі

Користувач вводить дані: матрицю суміжності або список вершин.
Перетворюємо введені дані в зручну для нас форму,тобто в масив даних де будуть зберігатися ребра, а саме дві вершини які з’єднані.
Створюємо масив шляху, в якому будуть записані вершини по яких ми проходили від початкової вершини до кінцевої включно, а також заносимо першу вершину в масив шляху.
Шукаємо усі можливі шляхи від початкової вершини до кінцевої.
1. Створюємо копію масиву шляху для подальшого користування.
2. Перевіряємо чи остання вершина вже є у масиві шляху, якщо так отже ми досягли кінця і друкуємо результат.
3. Якщо ні, шукаємо наступні вершини які з’єднані з останньою записаною вершиною у масиві шляху і ще не були пройдені. Якщо знаходимо тоді записуємо цю точку в масив шляху і повторюємо дії пункту 4.