5. Законы булевой алгебры и следствия из них.

Законы булевой алгебры.

Для удобства разобьем законы на четыре группы.

Первая группа.

1. (закон коммутативности для дизъюнкции).

2.

3. (первый закон поглощения).

4. (второй закон дистрибутивности).

5. (закон идемпотентности для дизъюнкции).

Следующие пять законов получаются заменой наи наоборот.

1. (закон коммутативности для конъюнкции).

2.(закон ассоциативности для конъюнкции).

3.(второй закон поглощения).

4.(первый закон дистрибутивности)

5.(закон идемпотентности для конъюнкции).

Каждый из законов 1- 5называется двойственным к соответствующему закону 1 – 5.

Вторая группа

1.

2.

3.

4.

5.

6.

Третья группа

1. (закон двойного отрицания).

2.

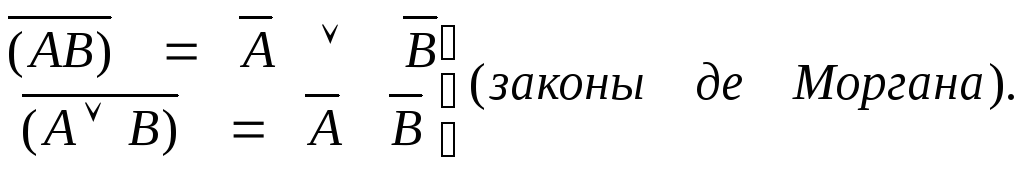
3.

Четвертая группа

1.

2. (закон контрапозиции).

3.

Следствия

Сформулируем некоторые полезные следствия из приведенных законов.

С1. Выбрасывая из произвольной дизъюнкции дизъюнктивные элементы равные нулю, мы не изменим величину этой дизъюнкции.

С2. Если в дизъюнкции хотя бы один из элементов равен 1, то вся дизъюнкция равна 1.

С3. Выбрасывая из произвольной конъюнкции все сомножители равные 1, мы не изменим ее величины.

С4. Если в конъюнкции хотя бы один сомножитель равен 0, то все произведение равно 0.

С5. Дизъюнкция или произведение любого числа одинаковых элементов равняется А.

Эти следствия можно доказать по индукции.

С6. Если А(а1, . . ., ап) произвольное выражение булевой алгебры, построенное из выражений а1, . . ., ап с помощью операций отрицания, дизъюнкции и конъюнкции, то отрицание этого выражения равняется , где В(а1,…,ап) получается из А с помощью замены всех умножений на дизъюнкции, а всех дизъюнкций на умножения, при условии сохранения всех имевшихся в А отрицаний.

С7. Если к некоторому выражению А булевой алгебры применено более чем одно отрицание, то, не меняя значения выражения, можно исключить любое четное число отрицаний.

6. Приведение к днф, кнф, сднф, скнф. Нормальные формы

Элементарной дизъюнкциейназывается выражение,представляющее собой дизъюнкцию любого конечного множества попарно различных между собой переменных, часть которых (возможна пустая) взята со знаком отрицания. К числу элементарных дизъюнкций будем также относить выражения, состоящие из одной переменной (с отрицанием или без), а также константу 0.

В силу определения:

являются элементарными дизъюнкциями, а

не являются.

Элементарным произведениемназывается выражение, представляющее собой произведение любого конечного множества попарно различных между собой переменных, над частью которых (быть может пустой) поставлен знак отрицания. К числу элементарных произведений также относятся выражения с одной переменной с отрицанием или без, а также константа 1.

Элементарные произведения:

Неэлементарные произведения:

Переменные и их отрицания называются первичными термамиилилитералами.

Дизъюнкция любого числа первичных термов равна либо 1, либо элементарной дизъюнкции. Произведение любого числа первичных термов равно либо 0, либо элементарному произведению.

Дизъюнктивной нормальной формой(ДНФ) называется дизъюнкция любого конечного множества попарно различных произведений.

Конъюнктивной нормальной формой(КНФ) называется произведение любого конечного множества попарно различных дизъюнкций.

Алгоритм приведения к ДНФ и КНФ заключается в следующем.

1. Преобразовать выражение в соответствии с операциями отрицания.

2. Использовать первый (ДНФ) или второй (КНФ) законы дистрибутивности.

Пример: Привести к ДНФ и КНФ выражение.

На первом этапе обрабатываем знаки отрицания:

Раскрывая скобки, приведем к ДНФ:

При приведении к КНФ последовательно применяем второй закон к первой скобке выражения

Рассмотрим некоторое множество М булевых переменных. В качестве такого множества будем выбирать множество аргументов той или иной булевой функции.

Элементарные дизъюнкции называются конституантами 0 для данного множества М булевых переменных, если они содержат в прямом либо инверсном виде все переменные множества М.

Элементарные конъюнкции называются конституантами 1 для данного множества М булевых переменных, если они содержат в прямом либо инверсном виде все переменные множества М.

Для переменных произвольную конституанту нуля можно представить в видеа произвольную конституанту 0 в видегдеозначает либо, либо. Условимся нумеровать конституанты нуля и единицы с помощью тех же номеров, что и соответствующие им наборы переменных.

ДНФ/КНФ называется совершенной (СДНФ/СКНФ), если все составляющие ее элементарные произведения/дизъюнкции являются конституантами единицы/нуля для одного и того же множества М переменных. СДНФ/СКНФ называется СДНФ/СКНФ булевой функции f, если она равна этой функции и если множество, составляющих ее переменных, совпадает с множеством аргументов функцииf.

Справедливо следующее: Любая булева функция имеет одну и только одну СДНФ/СКНФ.

Рассмотри процесс приведения к СДНФ/СКНФ.

Рассмотрим произвольную ДНФ от переменныхx₁, . . .,x_n. Пусть некоторые элементарные произведенияp, входящие в эту форму, не содержат какой либо переменнойx_j. Тогда эти произведения можно заменить равными им выражениями

Продолжая этот процесс относительно других переменных множества аргументов функции, не входящих в то или иное элементарное произведение, после повторения этой процедуры некоторое конечное число раз получим СДНФ выражения , поскольку в каждое составляющее ее элементарное произведение будут входить все переменные из множества аргументов функции.

Назовем этот процесс приведением ДНФ к совершенному виду.

Аналогичным образом можно построить процесс приведения КНФ к совершенному виду. Для этой цели к входящей в КНФ произвольной элементарной дизъюнкции q, не содержащей, например, переменной, добавляется равный нулю элемент. Затем к полученному выражению применяется второй дистрибутивный закон:

Продолжая по аналогии, мы сможем в каждую элементарную дизъюнкцию ввести все недостающие в ней переменные, после чего форма превратится в совершенную.

Пример: Выражение привести к СДНФ и СКНФ.

1.

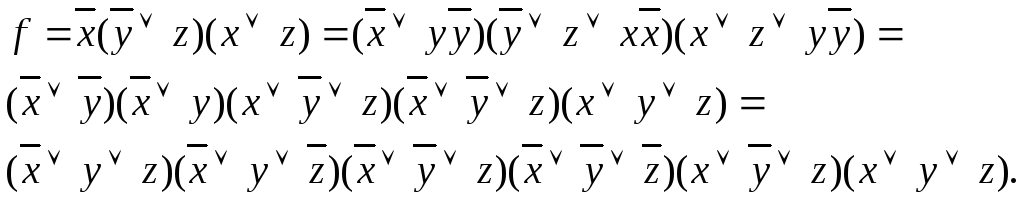
2.