23. Нечеткие множества.

Нечеткое множествопредставляет собой совокупность элементов произвольной природы, относительно которых нельзя с полной определенностью утверждать – принадлежит ли тот или иной элемент рассматриваемой совокупности данному множеству или нет. Другими словами, нечеткое множество отличается от обычного множества тем, что для всех, или части его элементов не существует однозначного ответа на вопрос: «Принадлежит или не принадлежит тот или иной элемент рассматриваемому нечеткому множеству»

Для построения нечетких моделей систем само понятие нечеткого множества следует определить строго, чтобы исключить неоднозначность толкования тех или иных его свойств. Наиболее естественным и интуитивно понятным является задание области значений подобной функции как интервал действительных чисел, заключенных между 0 и 1 (включая и сами эти значения).

Математическое определение нечеткого множества. Формально нечеткое множество определяется как множество упорядоченных пар или кортежей вида:, гдеявляется элементом некоторого универсального множества, или универсума, а– функция принадлежности, которая ставит в соответствие каждому из элементовнекоторое действительное число из интервала, т.е. данная функция определяется в форме отображения:

При этом значение для некоторогоозначает, что элементопределенно принадлежит нечеткому множеству, а значениеозначает, что элементопределенно не принадлежит нечеткому множеству.

Формально конечное нечеткое множество в общем случае имеет вид:

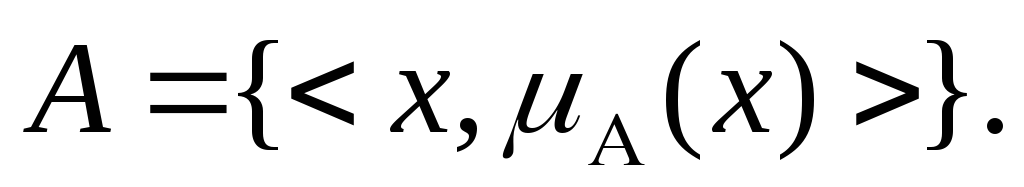
Универсум - это множество, содержащее в рамках некоторого контекста все возможные элементы. Формально удобно считать, что функция принадлежности универсума как нечеткого множества тождественно равна единице для всех без исключения элементов:.

Пустое нечеткое множество, или множество, которое не содержит ни одного элемента, обозначаетсяи формально определяется как такое нечеткое множество, функция принадлежности которого тождественно равна нулю для всех без исключения элементов:

Формальное определение нечеткого множества не накладывает никаких ограничений на выбор конкретной функции принадлежности для его представления. Однако на практике удобно использовать те из них, которые допускают аналитическое представление в виде некоторой простой математической функции. Это упрощает не только соответствующие численные расчеты, но и сокращает вычислительные ресурсы, необходимые для хранения отдельных значений этих функций принадлежности.

Функция принадлежности– математическая функция, определяющая степень, с которой элементы некоторого множества принадлежат заданному нечеткому множеству. Данная функция ставит в соответствие каждому элементу нечеткого множества действительное число из интервалаЗадать конкретное нечеткое множество означает определить соответствующую ему функцию принадлежности.

При построении функций принадлежности для нечетких множеств следует придерживаться некоторых правил, которые предопределяются характером неопределенности, имеющей место при построении конкретных нечетких моделей.

С практической точки зрения с каждым нечетким множеством удобно ассоциировать некоторое свойство, которое характеризует рассматриваемую совокупность объектов универсума. При этом по аналогии с классическими множествами рассматриваемое свойство может порождать некоторый предикат, который вполне естественно назвать нечетким предикатом. Данный нечеткий предикат может принимать не одно из двух значений истинности («истина» или «ложь»), а целый континуум значений истинности, которые для удобства выбираются из интервала При этом значению «истина» по-прежнему соответствует число 1, а значению «ложь» - число 0.

Содержательно это означает следующее: чем в большей степени элемент обладает рассматриваемым свойством, тем более близко к 1 должно быть значение истинности соответствующего нечеткого предиката. И наоборот, чем в меньшей степени элементобладает рассматриваемым свойством, тем более близко к 0 должно быть значение истинности этого нечеткого предиката. Если элементопределенно не обладает рассматриваемым свойством, то соответствующий нечеткий предикат принимает значение «ложь» (или число 0). Если же элементопределенно обладает рассматриваемым свойством, то соответствующий нечеткий предикат принимает значение «истина» (или число 1).

Тогда в общем случае задание нечеткого множества с использованием специального свойства эквивалентно заданию такой функции принадлежности, которая содержательно представляет степень истинности соответствующего одноместного нечеткого предиката.

Понятие нечеткого отношениянаряду с понятием самого нечеткого множества следует отнести к фундаментальным основам всей теории нечетких множеств. На основе нечетких отношений определяется целый ряд дополнительных понятий, используемых для построения нечетких моделей сложных систем.

Содержательно нечеткое отношение определяется как любое нечеткое подмножество упорядоченных кортежей, построенных из элементов тех или иных базисных множеств, в качестве которых в данном случае используются универсумы. При этом под кортежем, так же как и в случае обычных множеств, понимается произвольный набор или список упорядоченных элементов.

В общем случае нечетким отношением, заданном на множествах (универсумах) , называется некоторое фиксированное нечеткое подмножество декартова произведения этих универсумов. Другими словами, если обозначить произвольное нечеткое отношение через, то по определению, где- функция принадлежности данного нечеткого отношения, которая определяется как отображение. Черезобозначен кортеж изэлементов, каждый из которых выбирается из своего универсума:

.

Нечеткая логика, которая служит основой для реализации методов нечеткого управления, более естественно описывает характер человеческого мышления и ход его рассуждений, чем традиционные формально-логические системы. Именно поэтому изучение и использование математических средств, для представления нечеткой исходной информации позволяет строить модели, которые наиболее адекватно отражают различные аспекты неопределенности, постоянно присутствующей в окружающей нас реальности.

Нечеткая логика предназначена для формализации человеческих способностей к неточным или приближенным рассуждениям, которые позволяют более адекватно описывать ситуации с неопределенностью. Классическая логика по своей сути игнорирует проблему неопределенности, поскольку все высказывания и рассуждения в формальных логических системах могут иметь только значение «истина» (И,1) или значение «ложь» (Л,0). В отличие от этого в нечеткой логике истинность рассуждений оценивается в некоторой степени, которая может принимать и другие отличные значения. Нечеткая логика использует основные понятия теории нечетких множеств для формализации неточных знаний и выполнения приближенных рассуждений в той или иной предметной области.

В предложенной Л.Заде варианте нечеткой логики множество истинностных значений высказываний обобщается до интервала действительных значений , что позволяет высказыванию принимать любое значение истинности из этого интервала. Это численное значение является количественной оценкой степени истинности высказывания, относительно которого нельзя с полной уверенностью заключить о его истинности или ложности. Использование в качестве множества истинностных значений интервалапозволяет построить логическую систему, в рамках которой оказалось возможным выполнять рассуждения с неопределенностью и оценивать истинность высказываний.

Исходным понятием нечеткой логики является понятие элементарного нечеткого высказывания.

Элементарное нечеткое высказывание– это повествовательное предложение, выражающее законченную мысль, относительно которой мы можем судить об ее истинности или ложности только с некоторой степенью уверенности. В нечеткой логикестепень истинности элементарного нечеткого высказывания принимает значение из замкнутого интервала, причем 0 и 1 являются предельными значениями степени истинности и совпадают со значениями «ложь» и «истина» соответственно.

Нечеткая импликация или импликация нечетких высказываний А и В (читается – «ЕСЛИ А, ТО В») – называется бинарная логическая операция, результат которой является нечетким высказыванием, истинность которого может принимать значение, например, определяемое формулой предложенной Э.Мамдани:

Эту форму нечеткой импликации также называют нечеткой импликацией Мамданиили нечеткой импликациейминимума корреляции.

Классическая нечеткая импликация, предложенная Л.Заде:

Продукционные системы были разработаны в рамках исследований по методам искусственного интеллекта и нашли широкое применение для представления знаний и вывода заключений в экспертных системах, основанных на правилах. Поскольку нечеткий вывод реализуется на основе нечетких продукционных правил, рассмотрение базового формализма нечетких продукционных моделей приобретает самостоятельное значение. При этом нечеткие правила продукций не только во многом близки к логическим моделям, но и, что наиболее важно, позволяют адекватно представить практические знания экспертов в той или иной проблемной области.

Правило нечеткой продукции– под этим правилом понимается выражение вида:

где () – имя нечеткой продукции;- сфера применения нечеткой продукции;- условие применимости ядра нечеткой продукции;- ядро нечеткой продукции, в котором- условие ядра (или антецедент);- заключение ядра (или консеквент);- знак логической секвенции (или следования);- метод или способ определения количественного значения степени истинности заключения ядра;- коэффициент определенности или уверенности нечеткой продукции;- постусловия продукции.

Ядро продукции записывается в виде: , где А, В – некоторые выражения нечеткой логики, которые наиболее часто представляются в форме нечетких высказываний.

Продукционная нечеткая системапредставляет собой некоторое согласованное множество отдельных нечетких продукций в форме.