Правила вывода логики предикатов

Вывод представляет собой процедуру, которая из заданной группы выражений выводит, отличное от заданного выражение. Когда группа выражений, образующих посылку, является истиной, то должно гарантироваться, что выражение, выведенное из них в соответствии с правилом вывода, также является истиной.

В логике предикатов в качестве такого правила вывода используется правило, которое из двух выражений AиABвыводит новое выражениеB. Это правило называется правилом дедуктивного вывода.

Для описаний правил вывода во многих случаях используется нотация (как это указывалось выше), при которой над чертой записывается группа выражений, принимаемых за посылку, а под чертой – выражение, которое выводится:

Такой тип правила вывода носит название modusponens.

Можно многократно использовать одно и тоже правило вывода. Например, если помимо выражений A,ABсуществует выражениеBC, то можно вывестиC, дважды использовав приведенное правило. Получение выраженияприменением конечного числа раз правила вывода к заданной группе выраженийбудем записывать в виде:

При этом говорят, что дедуктивно выводится из. Очевидно, что из вышеуказанного, легко выводится еще одно правило:

12. Особенности использования кванторов.

Точность изложенного не гарантируется, т.к. в лекциях такого пункта не было.Но был фрагмент, где «кванторов» в тексте было оч. Много – его и вставил как ответ.

В качестве символов второго класса используются и. Эти символы называются кванторами общности и существования, соответственно. Переменная, которая квантифицирована, т.е. к ней применен один из кванторов, называется связанной. Квантор общности является обобщением, аналогом конъюнкции, а квантор существования – обобщением, аналогом дизъюнкции на произвольное, не обязательно конечное множество.

Действительно, пусть Тогда для любого предикатаUвыполняется:

Аналогом законов Де Моргана для кванторов являются:

Часто возникает ситуация, когда некоторые переменные связываются кванторами , а все другие -. В этом случае может возникнуть неоднозначность при интерпретации кванторов.

Пусть задан некоторый предикат U(x,y). Очевидно, что возможно восемь случаев связывания его кванторами существования и общности:

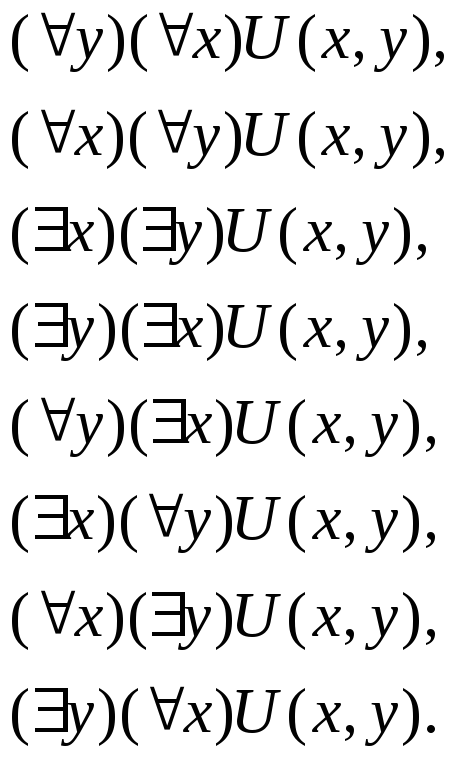
Необходимо дать интерпретацию этим восьми случаям.

Рассмотрим, например, предикат подсистема(x, y), который задает отношениеx подсистема y.Пусть переменнаяxсвязана квантором общности, аy– квантором существования. В этом случае существует две интерпретации: 1. «Для всехx, существуетy, для которыхxподсистема», 2. «Существуетy, что всеxего подсистемы».

Порядок следования связанных квантором переменных определяется при чтении предиката слева направо. Дадим интерпретацию для других значимых случаев, которые можно выразить этим предикатом и кванторами:

• (x)(y)подсистема(x, y) – все объекты являются подсистемами;

• (x)(y)подсистема(x,y) – существует объект, который является подсистемой любого объекта;

• (y)(x)подсистема(x, y) – для всякого объекта существует объект, являющийся его подсистемой;

• (x)(y)подсистема(x, y) – существует объект, который является чей-то подсистемой.

Сделаем некоторые важные обобщения.

1.Чтобы найти отрицание выражения, начинающегося с кванторов, надо каждый квантор заменить на его двойственный и перенести знак отрицания за кванторы. Отсюда:

2.Одноименные кванторы можно переставлять. Разноименные кванторы можно переставлять только в одну сторону. Отсюда:

Если то

Действительно, если существует объект, который является чьей-то подсистемой, то для каждого объекта будет существовать объект, являющийся его подсистемой.

Если то

Действительно, если существует y, что всеxего подсистемы, то для всехxсуществуетy, для которогоxподсистемы. Однако, перестановка в обратную сторону неверна. Например:

Если тонеобязательно.

Действительно, если для каждого объекта существует объект, являющийся его подсистемой, то это не означает, что существует объект, который является чьей-то подсистемой.

3.

Докажем эту равносильность.

В этой выкладке мы опирались на следующее утверждение: