30. Что такое нормальное распределение и почему оно играет особую роль в метрологии?

Наибольшее распространение получил нормальный закон распределения, называемый часто распределением Гаусса:

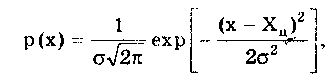(6.6)

где  — параметр рассеивания распределения, равный СКО; Х_ц — центр распределения, равный МО. Вид нормального распределения показан на рис. 6.3.

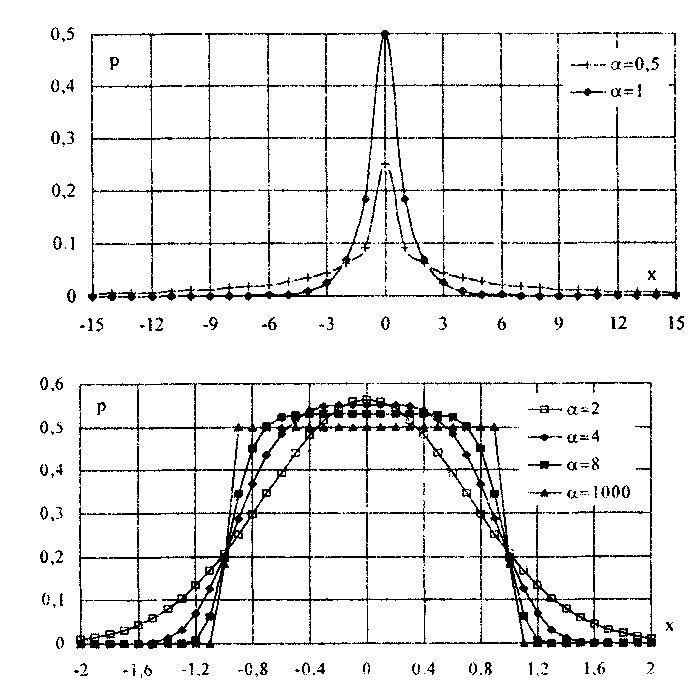
Рис. 6.6. Экспоненциальные распределения, определяемые по

формуле (6.5) при  = 1 и Х_ц = 0

Широкое использование нормального распределения на практике объясняется центральной предельной георемой теории вероятностей [48, 49], утверждающей, что распределение случайных погрешностей будет близко к нормальному всякий раз, когда результаты наблюдений формируются под действием большого числа независимо действующих факторов, каждый из которых оказывает лишь незначительное действие по сравнению с суммарным действием всех остальных.

Вид экспоненциальных распределений при различных значениях показателя а приведен на рис. 6.6.

При введении новой переменной t = (х-Х_ц)/ из (6.6) получается нормированное нормальное распределение, интегральная и дифференциальная функции которого соответственно равны:

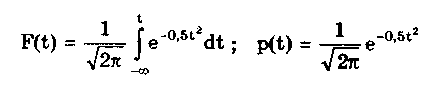
Нормирование приводит к переносу начала координат в центр распределения и выражению абсциссы в долях СКО. Значения интегральной и дифференциальной функций нормированного нормального распределения сведены в таблицы, которые можно найти в литературе по теории вероятностей [48, 49].

Определенный интеграл с переменным верхним пределом

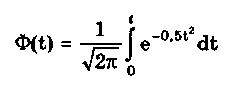(6.7)

называют функцией Лапласа. Для нее справедливы следующие равенства: Ф(- ) = - ,5; Ф(0) = 0; Ф(+ ) = 0,5; Ф(t) = -Ф(t). Функция Лапласа используется для определения значений интегральных функций нормальных распределений. Функция F(t) связана с функцией Лапласа формулой F(t) = 0,5 + Ф(t). Поскольку интеграл в (6.7) не выражается через элементарные функции, то значения функции Лапласа для различных значений t сведены в таблицу

31. Что такое доверительный интервал и каковы способы его задания?

Доверительным называется интервал, который с заданной надежностью покрывает оцениваемый параметр.

Рассмотренные точечные оценки параметров распределения дают оценку в виде числа, наиболее близкого к значению неизвестного параметра. Такие оценки используют только при большом числе измерений. Чем меньше объем выборки, тем легче допустить ошибку при выборе параметра. Для практики важно не только получить точечную оценку, но и определить интервал, называемый доверительным, между границами которого с заданной дове рителъной вероятностью

где q — уровень значимости; х_н, х_в— нижняя и верхняя границы интервала, находится истинное значение оцениваемого параметра.

В общем случае доверительные интервалы можно строить на основе неравенства Чебышева. При любом законе распределения случайной величины, обладающей моментами первых двух порядков, верхняя граница вероятности попадания отклонения случайной величины х от центра распределения Х_ц в интервал tS_x описывается неравенством Чебышева

где S_x — оценка СКО распределения; t — положительное число.

Для нахождения доверительного интервала не требуется знать закон распределения результатов наблюдений, но нужно знать оценку СКО. Полученные с помощью неравенства Чебышева интервалы оказываются слишком широкими для практики. Так, доверительной вероятности 0,9 для многих законов распределений соответствует доверительный интервал 1,6S_X. Неравенство Чебышева дает в данном случае 3,16S_X. В связи с этим оно не получило широкого распространения.

В метрологической практике используют главным образом кван-тильные оценки доверительного интервала. Под 100P-процентным квантилем х_р понимают абсциссу такой вертикальной линии, слева от которой площадь под кривой плотности распределения равна Р%. Иначе говоря, квантиль — это значение случайной величины (погрешности) с заданной доверительной вероятностью Р. Например, медиана распределения является 50%-ным квантилем х_0,5.

На практике 25- и 75%-ный квантили принято называть сгибами, или квантилями распределения. Между ними заключено 50% всех возможных значений случайной величины, а остальные 50% лежат вне их. Интервал значений случайной величины х между х_{0 05} и х_{0 95} охватывает 90% всех ее возможных значений и называется интерквантильным промежутком с 90%-ной вероятностью. Его протяженность равна d_0,9= х_0,95 - х_0,05.

На основании такого подхода вводится понятие квантильных значений погрешности, т.е. значений погрешности с заданной доверительной вероятностью Р — границ интервала неопределенности ± _Д = ± (х_р - х_1-р)/2 = ± d_p/2. На его протяженности встречается Р% значений случайной величины (погрешности), a q = (1- Р)% общего их числа остаются за пределами этого интервала.

Для получения интервальной оценки нормально распределенной случайной величины необходимо:

• определить точечную оценку МО х̅ и СКО S_x случайной величины по формулам (6.8) и (6.11) соответственно;

• выбрать доверительную вероятность Р из рекомендуемого ряда значений 0,90; 0,95; 0,99;

• найти верхнюю х_в и нижнюю х_н границы в соответствии с уравнениями

полученными с учетом (6.1). Значения х_н и х_в определяются из таблиц значений интегральной функции распределения F(t) или функции Лапласа Ф(1).

Полученный доверительный интервал удовлетворяет условию

(6.13)

где n — число измеренных значений; z_p — аргумент функции Лапласа Ф(1), отвечающей вероятности Р/2. В данном случае z_p называется квантильным множителем. Половина длины доверительного интервала называется доверительной границей погрешности результата измерений.