Несмещенные оценки с минимальной дисперсией

Определение.

Оценка одномерного параметра называется несмещенной оценкой с минимальной дисперсией, если

1. 

2. 

Сокращенно такую оценку называют НОМД.

Теорема о единственности НОМД.

Если НОМД существует, то она единственна почти наверное.

Доказательство.

Пусть и- две НОМД, тогда

тоже несмещена и по неравенству Коши-Буняковского

ее дисперсия

Так как оценки исходные оценки являются НОМД, то неравенство на самом деле является равенством и оценки ипочти наверное линейно связаны (опять неравенство Коши-Буняковского). Так как они несмещены, то они совпадают почти наверное.

Доказательство завершено.

Всегда ли существует НОМД?

Пусть -семейство пуассоновских распределений с параметром, и требуется оценить величину. Тогда, если бы несмещенная оценкасуществовала, то она бы удовлетворяла условию

что очевидно, невозможно, так как справа стоит бесконечно дифференцируемая, а слева разрывная в нуле функция по .

Построение НОМД с помощью полной достаточной статистики.

Если существует несмещенная оценкапараметраи полная достаточная статистика, то по теореме Рао-Блэкуэлла-Колмогорова получаем, что оценка

является НОМД.

Пример.

Нетрудно показать, что максимальное наблюдениеявляется полной достаточной статистикой для параметрав выборке из распределения. Действительно, если

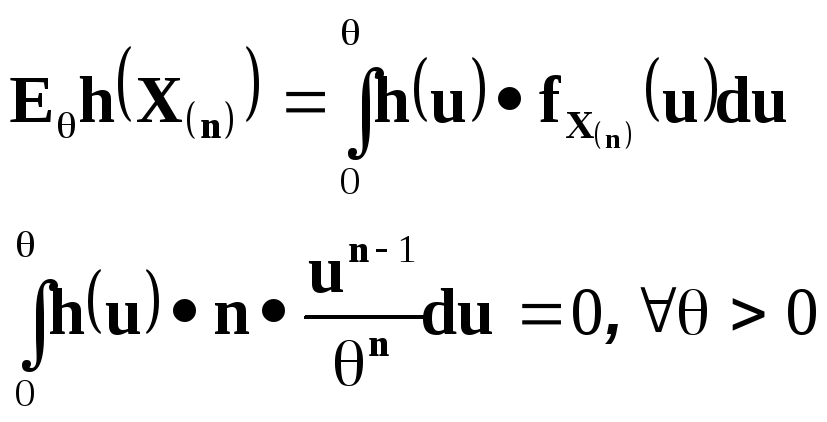
то, очевидно,

почти всюду по мере Лебега.

Для проверки полноты достаточной статистики часто можно использовать следующую теорему.

Теорема о полноте для экспоненциального семейства распределений

Пусть плотность распределения семейства можно представить в следующем виде

где все функции измеримы и образ отображения

содержитs– мерный параллелепипед. Тогда статистикаявляется полной достаточной статистикой для семейства

Доказательство этой теоремы опускаем.

В частности из этой теоремы следует, что среднее арифметическое является НОМД математического ожидания для нормального распределения

Эффективные оценки

В ряде случаев НОМД можно построить, исследуя отображение

, с точки зрения его информативности, – сколько информации о параметре содержит наблюдение c распределением?

Регулярные семейства распределений

Однопараметрическое семейство распределений назовем регулярным, если выполнены условия

1. Плотность дважды непрерывно дифференцируема по

2. 

3. Для любой несмещенной оценки

Свойства 2) и 3) выполняются, например, если можно менять местами интеграл по и производную по. Действительно

Все ли семейства регулярны?

Семейство нерегулярно – нарушено 2).

Теорема (Неравенство Рао-Крамера).

Пусть семейство регулярно, тогда для любой несмещенной оценкивыполнено неравенство

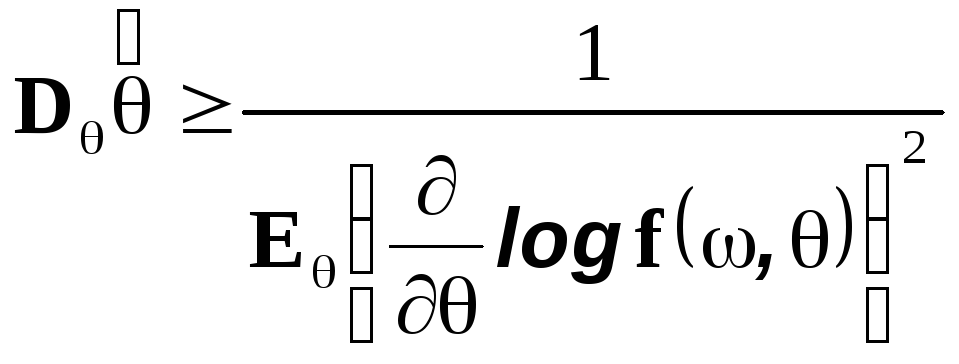
Доказательство.

Доказательство следует из неравенства Коши-Буняковского

Доказательство завершено.

Неравенство Рао-Крамера определяет нижнюю границу дисперсии для регулярных семейств

Определение.

Несмещенная оценка называется эффективной, если

Если оценка эффективна, то она НОМД. Обратное, вообще говоря, неверно.

Неравенство Коши-Буняковского превращается в равенство только при наличии линейной связи между функциями. Это позволяет дать простой критерий эффективности оценки: несмещенная оценка эффективна тогда и только тогда, когда

Информация по Фишеру.

Величина

называется информацией по Фишеру, содержащейся в наблюденииотносительно параметра. В классической статистической модели (или более общо в любойвыборке) информация по Фишеру (если она существует) пропорциональна количеству наблюдений:

Величинуназывают информацией по Фишеру, содержащейся в одном наблюдении.

Заметим, что