Выбор статистической модели

Выбор статистической модели для конкретных данных оказывает большое влияние на выводы. Наиболее содержательные выводы можно сделать в тех случаях, когда статистические данные представляют собой выборку. Если предположение о независимости и идентичности опытов не соответствует априорным сведениям, то, так или иначе, стараются либо представить исходные данные в виде некоторого преобразования (в этом случае уже ненаблюдаемой) выборки (см. далее линейная регрессионная модель), либо использовать другой вариант описания опыта, при котором можно реализовать идею накопления информации (см. далеемарковская цепь,пуассоновский процесс).

Соответствие статистической модели данным можно проверить с помощью специальных процедур математической статистики (см., например, далее критерии согласия). Основная идея такой проверки состоит в следующем. Выбирается множество данныхтакое, что вероятность попасть в это множество при существенных отклонениях от предложенной модели достаточно велика. Тогда событиеинтерпретируется как согласие данных с моделью, а событие, как несогласие. Множествоназывается обычно критическим множеством. Подробнее о статистических критериях далее в разделепроверка статистических гипотез.

Проверить качество статистических процедур и определить их характеристики можно, применяя статистическое моделирование с использованием компьютера. Для этого выбирается несколько распределений , для каждого из них с помощью компьютера моделируется несколько выборок и затем вычисляются и сравниваются теоретические и практические значения интересующих исследователя характеристик распределения. Хорошее согласие теории и практики на тестовых распределениях позволяет надеяться на такой же результат при реальных исследовании статистических данных.

Классическая статистическая модель.

Наиболее полно в математической статистике изучена классическая статистическая модель.

Определение.

Классической статистической моделью называется статистическая модель, в которой данные представляют собой числовую выборку

Эту выборку называют выборкой из распределения.

Оцениванию подлежит в этом случае неизвестная мера на прямой. Так как мераоднозначно определяется функцией распределения, то естественно следующее определение.

Плотность данных записывается в виде

где - плотность одного наблюдения.

Эмпирическая функция распределения

Определение.

Эмпирической функцией распределения называется случайная величина

Эмпирическая функция распределения является значением эмпирической меры на множестве и, следовательно, обладает следующими свойствами

1. Для любого фиксированного набора данных 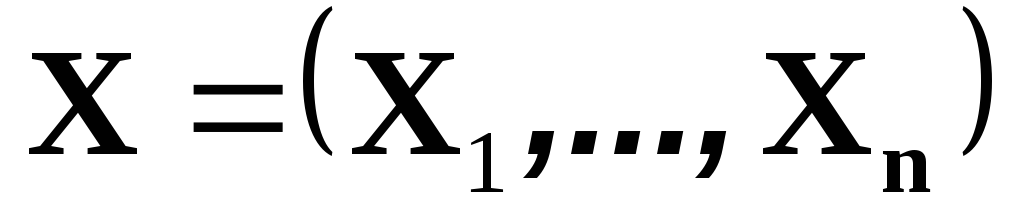она является функцией распределения.

2. Среднее значение данной функции распределения для любого , вычисленное в предположении, что неизвестная мера равна, равно

3. для любой меры.

Эмпирическая функция распределения реализует идею подстановки, и обладает также еще двумя важными свойствами, которые приводятся без доказательства.

Теорема Гливенко.

Теорема Колмогорова.

Если функция распределения данных непрерывна, то

,

где

Распределение случайной величины называется распределением Колмогорова, а функция распределенияназывается функцией распределения Колмогорова.