Методы построения доверительных множеств и интервалов

Для построения доверительных множеств используются случайные величины, свободные от распределения

Случайные величины, свободные от распределения

Определение.

Случайная величина называетсяслучайнойвеличиной свободной от распределения, если ее распределение одинаково для всех мер из семейства, т.е.

Если свободна от распределения, то выбрав множествотакое, что, получим, что множество

является доверительным множеством.

Таким образом, задача построения доверительных множеств сводится к задаче поиска случайных величин, свободных от распределения.

Примеры

1. Пусть . Тогда случайная величинасвободна от распределения и, следовательно,свободна от распределения.

2. Пусть . Тогда случайная величинасвободна от распределения и, следовательно,свободна от распределения.

3. Если функция распределения случайной величинынепрерывна, то случайная величинасвободна от распределения и, следовательно,свободна от распределения

В тех случаях, когда случайной величины, свободной от распределения не существует или ее трудно вычислить, используют случайные величины асимптотически свободные от распределения.

Асимптотические доверительные интервалы

Пусть - состоятельная и асимптотически нормальная оценка, например, оценка максимального прадоподобия или оценка, построенная по методу подстановки, т.е.

1. 

где функция и непрерывна. Тогда из свойств слабой сходимости и сходимости по вероятности следует, что

, т.е. случайная величинаасимптотически свободна от распределения и используя ее можно строить асимптотические доверительные интервалы.

Доверительные интервалы для параметров нормального распределения

Рассмотрим практически важный случай доверительного оценивания параметров нормального распределения. Для решения этой задачи необходимо построить случайные величины, свободные от распределения.

1. Пусть вектор данных представляет собой выборку из распределения. Тогдасвободна от распределения.

2. Пусть вектор данных представляет собой выборку из распределения. Тогдасвободна от распределения.

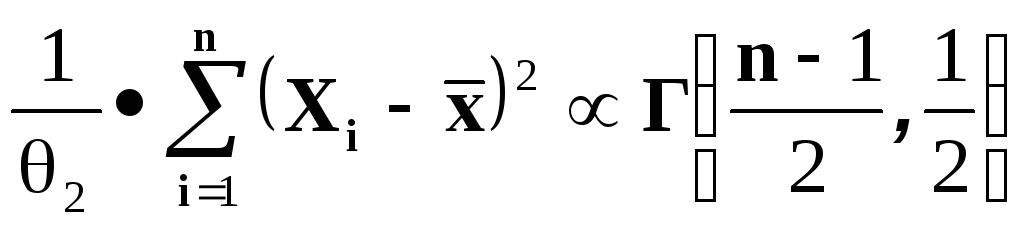3. Пусть вектор данных представляет собой выборку из распределения. Тогдасвободна от распределения и случайная величинасвободна от распределения. Последняя случайная величина имеет так называемое распределение Стьюдента сстепенью свободы c плотностью

Примеры решения статистических задач в общей статистической модели.

В данном разделе рассмотрены некоторые задачи, статистические данные в которых не являются выборкой. Во всех этих задачах явный вид оценок необходимо найти самостоятельно.

Линейная регрессионная модель

Пусть вектор данных имеет следующую структуру

где случайные величины - независимы, одинаково распределены и

Требуется оценить по данным значение. Для решения этой задачи применим метод максимального правдоподобия. Плотность данных имеет вид

Максимизируя данное выражение по получим

т.е. оценка максимального правдоподобия совпадает с оценкой метода наименьших квадратов.

Оценка матрицы переходных вероятностей конечной цепи Маркова

Пусть вектор данныхпредставляет собой реализацию простой конечной цепи Маркова с матрицей переходных вероятностей. Требуется построить оценки для элементов матрицыпо данным_.Для решения этой задачи применим метод максимального правдоподобия. Плотность данных имеет вид

где - количество переходов цепи Маркова из состоянияв состояниезашагов. Теперь

Оценка параметра пуассоновского процесса

Пусть - наблюдение пуассоновского процесса с параметромна интервалеТребуется построить оценку параметра. Для решения этой задачи найдем достаточную статистику. Заметим, что если- последовательные точки скачков пуассоновского процесса на интервале, то условное распределение векторапри условиисовпадает с распределением вариационного ряда построенного по независимым равномерно распределенным на интервалеслучайным величинам, т.е. не зависит от. Так как пуассоновский процесс однозначно определяется моментами своих скачков получаем, что случайная величинаравная числу точек процесса на интервалеявляется достаточной статистикой. Распределение этой величины пуассоновское с параметром. Следовательно она полная достаточная статистика и оценка- НОМД.