Проверка непараметрических гипотез. Критерии согласия

Если семейство илине является параметрическим, то соответствующая гипотеза называется непараметрической.

Рассмотрим следующую постановку задачи. Пусть вектор данных представляет собой выборку из распределения с функцией распределенияи необходимо проверить гипотезу

против альтернативы

В этом случае основная гипотеза простая, альтернатива непараметрическая.

Данная задача является задачей проверки согласия данных с гипотезой , а соответствующие критерии называются критериями согласия.

Общая идея построения критериев согласия следующая. Эмпирическая функция распределения представляет собой хорошую оценку для, следовательно значительные отклоненияотсвидетельствуют о справедливости гипотезы.

Поэтому, если определить расстояние между функциями распределения и-, то критическую область критерия согласия разумно выбрать в виде

где константа - выбирается из условия

В зависимости от выбора расстояния можно получить различные критерии согласия.

Критерий знаков

Положим

где - некоторая фиксированная точка.

Для того, чтобы рассчитать константу необходимо вычислить распределение расстоянияпри гипотезе. Это легко можно сделать, если заметить, что

Состоятельность критерия

Разумным требованием к критерию согласия является его состоятельность.

Определение.

Критерий объеманазывается состоятельным , если, для любой фиксированной простой альтернативы из

Очевидно, что критерий знаков не является состоятельным, потому что распределение расстояния одно и тоже для любой простой гипотезы си, следовательно, для всех таких альтернатив

Критерий Колмогорова

Рассмотрим расстояние

Это расстояние называется расстояние Колмогорова. Основанный на нем критерий называетсякритерием Колмогороваи используется, если функция распределения- непрерывна.

Состоятельность критерия Колмогорова и возможность рассчитать (асимптотически) распределение расстояния обеспечивается теоремой Колмогорова.

Действительно, если_,

то для того чтобы обеспечить фиксированный объем расстояниедолжно при гипотезестремиться к нулю по вероятности и, следовательно, стремится к нулю величинаДалее, расстояниек нулю не стремитсяи критерий является состоятельным.

Замечательным свойством критерия Колмогорова является независимость распределения расстояния от вида (непрерывной) функции распределения. Это следует из того, что

и

Критерий хи-квадрат

Для проверки согласия данных с гипотезой в общей выборочной моделииспользуется критерий хи-квадрат. Для этого множество элементарных исходовнеобходимо разбить нанепересекающихся частейи вычислить следующие величины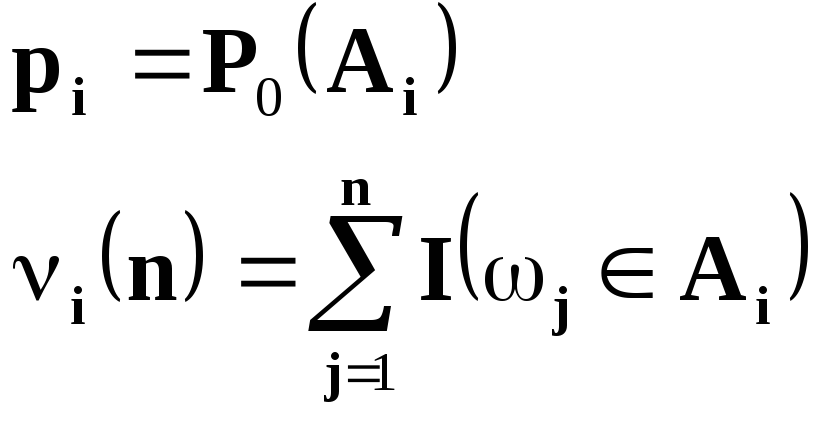

_{Критическое множество критерия хи-квадрат выглядит так}

Для расчета величины при большихиспользуется следующая теорема (без доказательства)

_{Теорема.}

Напомним , что распределение называется распределением хи-квадрат сстепенью свободы.

Точное распределение расстоянияможно получить используя тот факт, что распределение вектораявляется полиномиальным рапсределением.

Построение доверительных множеств и интервалов Постановка задачи

В ряде случаев необходимо указать множество, которому с заданной вероятностью принадлежит оцениваемый параметр.

Определение.

Пусть - параметрическое семейство. Случайное множествоназываетсядоверительным множествомсуровнем доверия, если

Если множествопредставляет собой интервал на действительной прямой, то оно называетсядоверительный интервал.