Домашнее задание

Задача 1

Величина y связана со значениями х₁ и х₂ зависимостью y = х₁ - х₂.

Определите допустимые значения абсолютных и относительных погрешностей измерения величин х₁ и х₂ для обеспечения косвенного измерения y с относительной погрешностью не более ± 1%. Максимальные значения х₁ и х₂ составляют 100 ед. и 50 ед. соответственно. Суммарные систематические погрешности соизмеримы со случайными погрешностями. Предполагается нормальный закон распределения случайных и систематических погрешностей.

Задача 2

Величина y связана со значениями х₁ и х₂ зависимостью y = . Определите допустимые значения абсолютных и относительных погрешностей измерения величин х₁ и х₂ для обеспечения косвенного измерения y с относительной погрешностью не более ± 1%. Максимальные значения х₁ и х₂ составляют 100 ед. и 50 ед. соответственно. Суммарные систематические погрешности соизмеримы со случайными погрешностями. Предполагается нормальный закон распределения случайных и систематических погрешностей.

Задача 3

Величина y связана со значениями х₁ и х₂ зависимостью y = 1/5 ∙х₂.

Определите допустимые значения абсолютных и относительных погрешностей измерения величин х₁ и х₂ для обеспечения косвенного измерения y с относительной погрешностью не более ± 1%. Максимальные значения х₁ и х₂ составляют 100 ед. и 50 ед. соответственно. Суммарные систематические погрешности соизмеримы со случайными погрешностями. Предполагается нормальный закон распределения случайных и систематических погрешностей.

Задача 4

Величина y связана со значениями х₁ и х₂ зависимостью y = х₁ + х₂. Определите допустимые значения абсолютных и относительных погрешностей измерения величин х₁ и х₂ для обеспечения косвенного измерения y с абсолютной погрешностью не более Δ y = 1,5 ед. Максимальные значения х₁ и х₂ составляют 100 ед. и 50 ед. соответственно. Суммарные систематические погрешности соизмеримы со случайными погрешностями. Предполагается нормальный закон распределения случайных и систематических погрешностей.

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 6

Тема: Аппроксимация результатов эксперимента. Метод опорных точек

Аппроксимация результатов эксперимента. Аппроксимации экспериментальных результатов должно предшествовать изучение характера их поведения на определенном участке изменения аргумента и его сопоставление с характером изменения хорошо изученных функций. Вид аппроксимирующей функции Р(х) выбирается на основе этого сопоставления, а если возможно, то и исходя из условия соответствия физической природе явления или имеющимся представлениям об особенностях поведения исследуемой величины.

Близость значений функции Р(х) и экспериментальных результатов φ(x_i) в точках x = x_i обеспечивается введением в аппроксимирующую функцию n свободных параметров a_n и соответствующим их выбором.

Существуют два различных способа нахождения свободных параметров. Выбор того или иного из них определяется целями и задачами, стоящими перед исследователем, точностью полученных результатов, их количеством и т.д.

Первый способ базируется на удовлетворении условию, чтобы функция Р(х, а) совпадала с экспериментальными значениями в n точках, выбранных в качестве опорных (число свободных параметров не должно превышать числа имеющихся опытных точек). В этом случае для определения n неизвестных значений параметров a_n используется система n уравнений

(1)

После определения численных значений параметров а_n проверяется качество аппроксимации путем сопоставления значений функции и экспериментальных данных в оставшихся точках х_i рассматриваемого интервала. Если обнаруженные между ними расхождения превышают допустимые по условиям точности, то аппроксимацию следует повторить, приняв в качестве опорных другие точки или увеличив число свободных параметров.

В предельном случае, когда число свободных параметров равно числу экспериментальных точек в рассматриваемом интервале изменения аргумента, все экспериментальные точки будут совпадать со значениями функции. Следует заметить, что добиваться точного совпадения значений функции и экспериментальных данных путем значительного увеличения числа свободных параметров часто неразумно, поскольку экспериментальные результаты получены с большей или меньшей погрешностью, и такая функция может не отражать действительного характера изменения исследуемой величины (кривая 1 на рис. 1). На этом рисунке σ – среднеквадратичная погрешность результатов эксперимента.

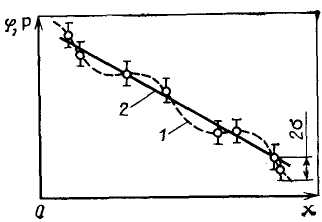
Рис. 1. Аппроксимация опытных данных представленных точками:

1 – аппроксимирующая функция с большим числом свободных параметров;

2 – аппроксимирующая функция с небольшим числом свободных параметров.

Система (1) представляет собой систему n уравнений первой степени с n неизвестными значениями параметров а_n .Величины N, х_i, φ(х_i) известны из эксперимента. При n≤N система имеет единственное решение, которое может быть получено с использованием ЭВМ. При n = N численные значения свободных параметров, определенных по первому и второму способам, идентичны, а все опытные точки совпадают с аппроксимирующей зависимостью. При n > N система уравнений переопределена и допускают множество решений. Стремиться к значительному увеличению числа свободных параметров обычно нецелесообразно не только из-за существенного усложнения аппроксимирующей функции и ее дальнейшего использования, но и из-за того, что хорошее сглаживание погрешностей эксперимента будет иметь место лишь в случае n  N. В то же время для удовлетворительного описания достаточно сложного характера изменения определенной опытным путем величины требуется увеличить число n.

Оптимальное число свободных параметров определяют из условия , где – среднеквадратичное отклонение опытных точек от аппроксимирующей зависимости  – среднеквадратичная погрешность эксперимента.

Условие _n  σ означает, что математическая погрешность аппроксимации много больше погрешности опытных данных, поэтому следует увеличить число свободных параметров. При _n  σ часть свободных параметров недостоверна и надо уменьшить n. Если при выбранном, исходя из указанных соображений, значении n выполняется условие n  N, то вид аппроксимирующей функции выбран удачно. При n  N следует подобрать более подходящий вид аппроксимирующей функции.