Тезисы лекций Тема №1. Случайные события

Цель лекции: Познакомить студентов с основными понятиями теории вероятности.

Перечень вопросов, выносимых для рассмотрения:

1. Случайное событие.

2. Классическое определение вероятности. Элементы комбинаторики.

3. Теоремы сложения и умножения вероятностей.

4. Формула полной вероятности. Формула Байеса.

Определение. Случайным событием называется событие, которое при осуществлении определенного комплекса условий может произойти или не произойти.

Под комплексом условий подразумевается, что произведен опыт (испытание), результат которого можно наблюдать.

Определение. Событие называется достоверным, (невозможным) если в результате опыта оно обязательно произойдет ( не произойдет).

Определение. События А и В называются совместными (несовместными), если они могут (не могут) произойти одновременно.

Определение. Событие А называется благоприятствующим событию В, если в результате появления А произойдет и событие В.

Определение. Событие , заключающееся в том, что не произошло событие А, называется противоположным событию А.

Определение. Множество событий называется полной группой, если в результате испытания произойдет хотя бы одно из них.

Определение. Элементарные события, которые могут произойти в результате опыта, называются исходами опыта.

Определение. Суммой двух событий А и В называется событие С=А+В, заключающееся в том, что произошло хотя бы одно из них.

Определение. Произведением двух событий А и В называется событие Д=А×В, заключающееся в том, что произошли оба события.

Определение. Классической вероятностью события А называется величина , где n - число равновозможных попарно несовместных исходов опыта, а m - число исходов, благоприятствующих появлению события А.

Определение. Относительной частотой события А называется величина , где n - число испытаний, а m - число появления события А в n испытаниях.

В статистике в качестве вероятности события принимают его относительную частоту.

Определение. Перестановками из n элементов называются комбинации по n элементов, отличающиеся друг от друга порядком расположения элементов.

Число подстановок из n элементов равно (эн факториал).

Определение. Сочетаниями из n элементов по m называются комбинации по m элементов, отличающиеся друг от друга составом (хотя бы одним элементом).

Число сочетаний

Определение. Размещениями из n элементов по m называются комбинации по m элементов, отличающиеся друг от друга либо составом, либо порядком расположения элементов.

Число размещений .

Теорема 1. , если А, В несовместны.

Теорема 2. - , если А, В совместны.

Теорема 3. , если А, В независимы.

Теорема 4. , если А, В зависимы, где - вероятность события В при условии, что произошло событие А.

Следствие 1.

Следствие 2. Вероятность появления хотя бы одного из независимых событий равна , где =

Если событие А, может наступить лишь при появлении одного из несовместных событий (гипотез) , образующих полную группу несовместных событий, то по формуле полной вероятности

Вероятность гипотезы при условии, что событие А произошло, определяется по формуле Байеса

,

где - полная вероятность события А.

Вопросы для самопроверки:

1. Что называется случайным событием?

2. Какое событие называется достоверным, невозможным, благоприятствующим, противоположным?

3. Какие события называются совместными и несовместными?

4. Что называется полной группой событий?

5. Дайте определение суммы и произведения событий.

6. Что называется относительной частотой события?

7. Сформулируйте классическое определение вероятности события.

8. Какие комбинации называются перестановками, сочетаниями, размещениями?

9. Сформулируйте теоремы сложения вероятностей для несовместимых и совместимых событий.

10. Сформулируйте теоремы умножения вероятностей для зависимых и независимых событий.

11. Вероятность противоположного события.

12. Вероятность появления хотя бы одного события.

13. Напишите формулы полной вероятностей и Байеса.

Тема №2. Повторные независимые испытания

Цель лекции: Определение вероятности возможных событий при повторении независимых испытаний.

Перечень вопросов, выносимых для рассмотрения:

1. Формула Бернулли.

2. Локальная формула Лапласа.

3. Формула Пуассона.

4. Интегральная формула Лапласа.

Схемой Бернулли называется последовательность независимых испытаний, в каждом из которых может появиться событие А с одинаковой вероятностью .

Вероятность того, что в n независимых испытаниях события А появится k раз, определяется по формуле Бернулли:

, где которая на практике применяется при небольших n;

_{Если число испытаний большое, то вероятность определяется по формулам} Лапласа и Пуассона:

_, где , - локальная формула Лапласа;

, где = , - формула Пуассона, которая применяется при малых р (редкие события) и при достаточно больших n .

Вероятность того, что в n независимых испытаниях событие А появится от до раз включительно определяется по интегральной формуле Лапласа

- , где 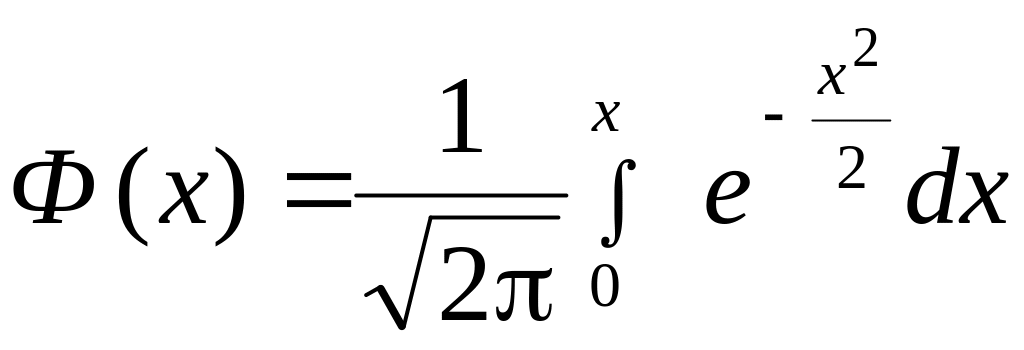- функция Лапласа.

Замечание 1. Формулы Лапласа и Пуассона дают приближенное значение вероятности, точность которых растет с увеличением n.

Замечание 2. Значения функций и Ф (х) приведены в таблицах, которые имеются практически во всех учебниках, задачниках, пособиях по теории вероятностей и математической статистике. При этом необходимо учитывать, что четная функция, а Ф (х) – нечетная.

Вопросы для самопроверки:

1. В чем суть повторных независимых испытаний.

2. Напишите формулу Бернулли. В каких случаях она применяется?

3. Напишите локальную формулу Лапласа.

4. Напишите формулу Пуассона.

5. Напишите интегральную формулу Лапласа.

6. Чем отличается формулы Лапласа и Пуассона от формулы Бернулли?

7. В чем отличие локальной и интегральной формул Лапласа?

Тема №3. Дискретные случайные величины

Цель лекции: Ввести понятие дискретных случайных величин и их числовых характеристик.

Перечень вопросов, выносимых для рассмотрения:

1. Определение случайной величины.

2. Закон распределения случайной величины.

3. Основные законы распределения дискретной случайной величины.

4. Числовые характеристики дискретной случайной величины.

Определение. Величина называется случайной, если в результате испытания она примет лишь одно возможное значение, заранее неизвестное и зависящее от случайных причин.

Определение. Дискретной случайной величиной называется величина, значения которой образуют счетное множество (множество, элементы которого можно пронумеровать).

Определение. Законом распределения вероятностей случайной величины называется закон, устанавливающий соотношение между возможными значениями случайной величины и соответствующими вероятностями.

Закон распределения дискретной случайной величины, как правило, задается в виде таблицы

			. . .
			. . .

где =1.

Пример 1. В денежной лотерее на 100 билетов разыгрывается один выигрыш в 20000 тенге, два выигрыша по 10000 тенге и 10 выигрышей по 1000 тенге. Найти закон распределения случайной величины Х - возможного выигрыша на один билет.

Решение. Возможные значения Х: х₁=20000, х₂=10000, х₃ =1000, х₄=0. Соответственно их вероятности равны: р₁=0,01, р₂=0,02, р₃=0,1, р₄=1 – ( р₁ + р₂ + р₃) = 1 – 0,13 = 0,87. Таким образом, искомый закон распределения имеет вид

	20000	10000	1000	0
	0,01	0,02	0,1	0,87

Случайные величины распределяется по классам, каждый из которых имеет определенный закон распределения, рассмотрим некоторые виды распределения дискретных случайных величин.

1. Биномиальный закон распределения. По этому закону распределяется случайная величина Х - число появления события в n независимых испытаниях. Она может принимать значения 0,1,2,…, m,…, n

с вероятностями

, где m =0,1,…, n.

2. Закон распределения Пуассона. Х - число появления редкого события в n независимых испытаниях, для которого вероятность

, где = , m =0,1,…, n.

3. Геометрический закон распределения. Х - число испытаний до первого появления события в n независимых испытаниях. Она принимает значения 1,2,…, m,… с вероятностями

, где m =1,2,…

4. Гипергеометрический закон распределения. Пусть среди N объектов М обладает альтернативным свойством. Тогда Х – число элементов, обладающих этим свойством среди n наугад взятых. Вероятность того, что Х примет значение m, равна ,

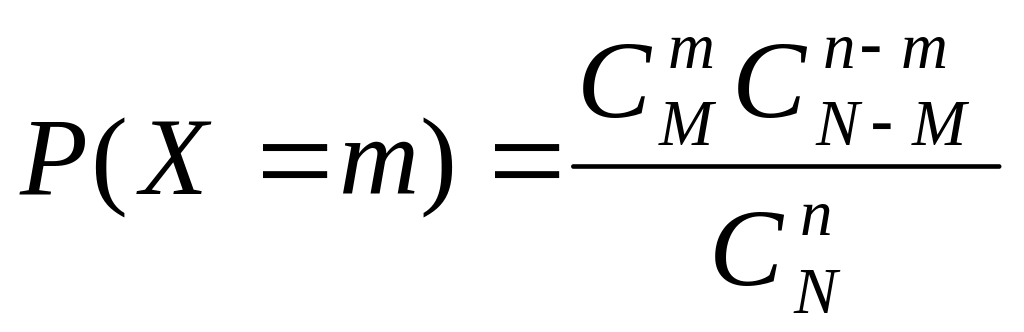где m =0,1,2,…, min(n;M).

Определение. Математическим ожиданием дискретной случайной величины называется сумма произведений возможных значений случайной величины на соответствующие вероятности:

Определение. Разность между случайной величиной и ее математическим ожиданием называется отклонением: = Х – М(Х)

Определение. Дисперсией случайной величины называется математическое ожидание квадрата отклонения величины от её математического ожидания: = М[X - M(X)]².

Дисперсию удобно вычислять по формуле:

Определение. Средним квадратическим отклонением случайной величины называется значение, равное квадратному корню из дисперсии: .

_{Основные свойства математического ожидания и дисперсии:}

1. _{М(С) = С}

2. _{М(СХ) = С М(Х)}

3. _{М(ХУ) = М(Х) М(У)}

4. _{М(ХУ) = М(Х)  М(У)}

5. _{D(С) = 0}

6. _{D(СХ) = С}²_D(Х)

7. _{D(ХУ) = D(Х) + D(У)}

Закон распределения	Биномиальный	Пуассоновский	Геометрический
Математическое ожидание	M(X)=np	M(X)=	M(X)=1/р
Дисперсия	D(X)=npq	D(X)=	D(X)=

Вопросы для самопроверки:

1. Дайте определение случайной величины.

2. Какие случайные величины называются дискретными?

3. Что называется законом распределения случайной величины?

4. Укажите основные законы распределения дискретной случайной величины.

5. Что называется математическим ожиданием дискретной случайной величины?

6. Что называется дисперсией случайной величины?

7. Что называется средним квадратическим отклонением случайной величины?

Тема №4. Непрерывные случайные величины

Цель лекции: Ознакомить с законами распределения и характеристиками непрерывных случайных величин.

Перечень вопросов, выносимых для рассмотрения:

1. Определение непрерывной случайной величины.

2. Функция распределения случайной величины и ее свойства.

3. Плотность распределения случайной величины и ее свойства.

4. Основные законы распределения непрерывных случайных величин.

5. Числовые характеристики непрерывной случайной величины.

Определение. Непрерывной случайной величиной называется величина, которая может принимать любые значения из некоторого конечного или бесконечного интервала.

Закон распределения НСВ может быть задан в виде функции распределения или плотности распределения вероятностей.

Определение. Функцией распределения вероятностей случайной величины Х называется функция определяющая для каждого значения х вероятность того, что случайная величина Х примет значение, меньшее х, т.е. .