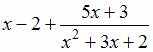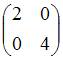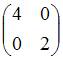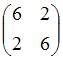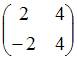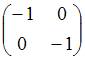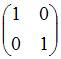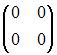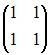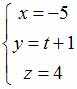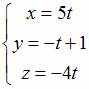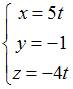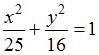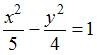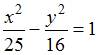- •2)Тема: Дробно-рациональные функции
- •4)Тема: Линейные отображения
- •1) Тема: Дифференциальная геометрия поверхностей
- •3)Тема: Особые точки функции комплексного переменного:
- •4)Тема: Операции над комплексными числами
- •Информатика вариант 1
- •Информатика вариант 2
- •Решение:
- •Тесты по дисциплине «информатика»
- •1. Раздел. Понятие информации. Общая характеристика процессов сбора, передачи, обработки и накопления информации
- •Тема 1.1. Информатика. Предмет информатики. Основные задачи информатики
- •Уровень I (базовый)
- •Уровень III (высокий)
- •Тема 1.2. Понятие информации, её измерение, количество и качество информации. Формы и способы представления информации
- •Уровень I (базовый)
- •Уровень III (высокий)
- •37. Задание
- •39. Задание
- •40. Задание
- •41. Задание
- •Тема 1.3. Информация и информационные технологии.
- •Уровень I (базовый)
- •3. Задание
- •Уровень II (средний)
- •Уровень III (высокий)
- •30. Задание
- •Тема 1.4. Кодирование информации. Системы счисления
- •Уровень I (базовый)
- •Уровень II (средний)
- •Уровень III (высокий)
- •2. Раздел Технические средства реализации информационных процессов
- •Тема 2.1. Состав и назначение основных элементов персонального компьютера. Периферийные устройства. Понятие и основные виды архитектуры эвм. Их характеристики
- •Уровень II (средний)
- •Уровень III (высокий)
- •Тема 2.2 Центральный процессор, системные шины
- •Уровень I (базовый)
- •Уровень II (средний)
- •Уровень III (высокий)
- •Уровень I (базовый)
- •Уровень II (средний)
- •Уровень III (высокий)
- •Уровень I (базовый)
- •Уровень II (средний)
- •Уровень III (высокий)
- •Раздел 3. Программные средства реализации информационных процессов. Офисные программные средства
- •Темы 3.1, 3.2, 3.3 Понятие системного программного обеспечения. Операционная система. Личное и корпоративное информационное обеспечение. Человеко-машинный интерфейс
- •Уровень I (базовый)
- •Уровень II (средний)
- •Уровень III (высокий)
- •Тема 3.2 Системы компьютерной графики
- •Уровень I (базовый)
- •Уровень II (средний)
- •Уровень III (высокий)
- •Раздел 4. Офисные приложения
- •Тема 4.1 Файловая структура. Служебное по. Операционные системы
- •Уровень I (базовый)
- •Уровень II (средний)
- •Уровень III (высокий)
- •Тема 4.2 Текстовые редакторы
- •Уровень I (базовый)
- •Уровень II (средний)
- •Уровень III (высокий)
- •Тема 4.3 Электронные таблицы
- •Уровень I (базовый)
- •Уровень II (средний)
- •Уровень III (высокий)
- •Тема 4.4 Электронные презентации
- •Уровень I (базовый)
- •Уровень II (средний)
- •Уровень III (высокий
- •Раздел 5. Модели решения функциональных и вычислительных задач
- •Уровень I (базовый)
- •Уровень II (средний)
- •Уровень III (высокий)
- •Раздел 6. Алгоритмизация и программирование. Технологии программирования. Языки программирования высокого уровня
- •Уровень I (базовый)
- •Уровень II (средний)
- •Уровень III (высокий)
- •Раздел 7. Языки программирования высокого уровня
- •Уровень I (базовый)
- •Уровень II (средний)
- •Уровень III (высокий)
- •Раздел 8. Базы данных
- •Уровень I (базовый)
- •Уровень II (средний)
- •Уровень III (высокий)
- •А) простым
- •Раздел 9. Локальные и глобальные сети эвм
- •Тема 9.1, 9.2 Основы компьютерной коммуникации. Принципы построения сетей, Компьютерные коммуникации и коммуникационное оборудование
- •Уровень I (базовый)
- •Правильные варианты ответа: сеть;
- •Уровень II (средний)
- •Уровень III (высокий)
- •Тема 4.3, 4.4 Сетевой сервис и сетевые стандарты. Программы для работы в сети Интернет. Документы Интернет
- •Уровень I (базовый)
- •Уровень II (средний)
- •Уровень III (высокий)
- •Тема 4.4. Защита информации в локальных и глобальных компьютерных сетях. Шифрование данных. Электронная подпись
- •Уровень I (базовый)
- •Уровень II (средний)
- •46. Задание
- •47. Задание
- •48. Задание
- •Уровень III (высокий)
ДЕ1.Абстрактная алгебра
1)Тема: Группы и подгруппы Группу по сложению образует множество …
|
целых чисел |
натуральных чисел |
|
натуральных чисел с нулем |
|
действительных чисел без нуля |
|
2)Тема: Дробно-рациональные функции
Разложение
дробно-рациональной функции
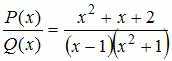 на
простые дроби над полем вещественных
чисел имеет вид …
на
простые дроби над полем вещественных
чисел имеет вид …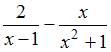
Решение:
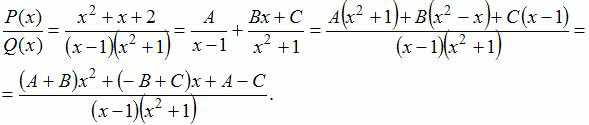
Получаем
систему трех уравнений с тремя
неизвестными:
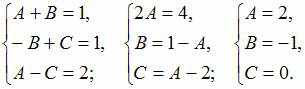
Тогда
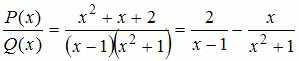
3)Тема: Основные алгебраические структуры В кольце квадратных матриц второго порядка единичный элемент … – это матрица
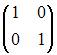
4)Тема: Линейные отображения
Пусть
![]() базис
пространства
базис
пространства
![]() Операторы
Операторы![]() и
и![]() этого
пространства заданы матрицами
этого
пространства заданы матрицами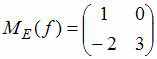
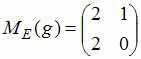 .
Тогда матрица оператора
.
Тогда матрица оператора
![]() равна
равна
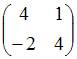
Решение:

Тема: Дробно-рациональные функции Разложение дробно-рациональной функции на простые дроби над полем вещественных чисел имеет вид …
Тема:
Линейные отображения
Линейный
оператор
отображает
базис
![]() в
векторы:
в
векторы:
![]()
![]()
![]() Тогда
матрица оператора
в
этом базисе имеет вид …
Тогда
матрица оператора
в
этом базисе имеет вид …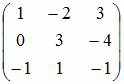
Решение:
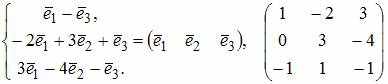
Тема: Основные алгебраические структуры В кольце целых четных чисел единичный элемент …
|
не существует |
Решение: В кольце целых четных чисел единичный элемент не существует.
Тема: Группы и подгруппы Группу по умножению образует множество …
|
действительных чисел без нуля |
действительных чисел |
|
целых чисел |
|
натуральных чисел с нулем |
|
Решение: Группу образует множество действительных чисел без нуля с введенной операцией умножения чисел. Все остальные множества групп не образуют, так как, например, нуль не имеет обратного элемента.
Тема: Группы и подгруппы Операция «+» – сложения образует группу на множестве …
|
целых четных чисел |
натуральных чисел |
|
целых нечетных чисел |
|
действительных чисел без нуля |
|
Решение:
Множество
целых четных чисел с введенной операцией
сложения образует группу. Множество
натуральных чисел не группа, так как,
например,
![]() не
имеет противоположного элемента.
Множество целых нечетных не имеет
нулевого элемента, как и множество
действительных чисел без нуля.
не
имеет противоположного элемента.
Множество целых нечетных не имеет
нулевого элемента, как и множество
действительных чисел без нуля.
Тема:
Линейные отображения
Из
заданных операторов пространства
![]() –
пространства трехмерных векторов,
линейным является оператор …
–
пространства трехмерных векторов,
линейным является оператор …![]()
Тема: Основные алгебраические структуры В кольце целых четных чисел единичный элемент …
|
не существует |
равен
|
|
равен |
|
равен
|
|
Решение: В кольце целых четных чисел единичный элемент не существует.
Тема:
Основные алгебраические структуры
Подалгеброй
алгебры
![]() является
совокупность …
является
совокупность …
|
|
|
|
|
|
|
|
Решение:
Совокупности
![]() и
не
являются подалгебрами алгебры
,
так как,
и
не
являются подалгебрами алгебры
,
так как,
![]() .
Совокупность
.
Совокупность
![]() не
является подалгеброй алгебры
,
так как множество
не
является подалгеброй алгебры
,
так как множество
![]() не
замкнуто относительно умножения.
Совокупность
является
подалгеброй алгебры
,
так как
не
замкнуто относительно умножения.
Совокупность
является
подалгеброй алгебры
,
так как
![]() и
множество
и
множество![]() замкнуто относительно умножения.
замкнуто относительно умножения.
Тема: Группы и подгруппы Подгруппой группы целых чисел с введенной операцией сложения является множество …
|
четных целых чисел |
нечетных целых чисел |
|
натуральных чисел |
|
натуральных чисел с нулем |
|
Тема:
Дробно-рациональные функции
Множество
всех дробно-рациональных функций
образует поле
![]() относительно
обычных операций сложения и умножения
таких функций.
Пусть
относительно
обычных операций сложения и умножения
таких функций.
Пусть
![]() и
и
![]() ,
причем
,
причем
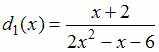 и
и
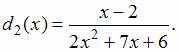 Тогда
числитель произведения
Тогда
числитель произведения
![]() равен
…
равен
…
|
1 |
|
|
|
|
|
|
Решение:
Разложим
на линейные множители знаменатели
дробно-рациональных функций
![]() и
и
![]() :
:
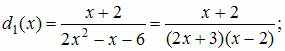
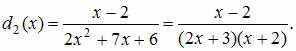 Тогда
Тогда
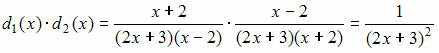 .
То
есть числитель произведения
равен
1.
.
То
есть числитель произведения
равен
1.
Тема:
Дробно-рациональные функции
Разложение
дробно-рациональной функции
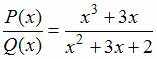 на
элементарные дроби имеет вид …
на
элементарные дроби имеет вид …
|
|
|
|
|
|
|
|
Решение:
Выполним
деление заданных полиномов
«уголком»:
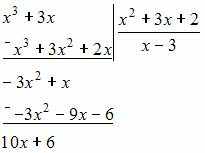 Разложим
знаменатель на простые множители:
Разложим
знаменатель на простые множители:
![]() .
Тогда
.
Тогда
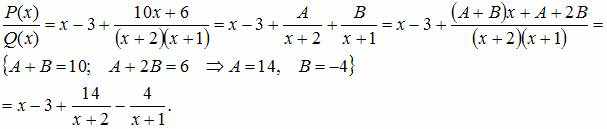
Тема: Группы и подгруппы Группу по умножению образует множество …
|
действительных чисел без нуля |
действительных чисел |
|
целых чисел |
|
натуральных чисел с нулем |
|
Решение: Группу образует множество действительных чисел без нуля с введенной операцией умножения чисел. Все остальные множества групп не образуют, так как, например, нуль не имеет обратного элемента.
Тема: Линейные отображения Из заданных операторов пространства – пространства трехмерных векторов, линейным является оператор …
|
|
|
|
|
|
|
|
Решение:
Линейным
называется отображение
![]() удовлетворяющее
условиям:
удовлетворяющее
условиям:
![]() ,
,
![]() .
Проверим
на линейность оператор
.
Проверим
на линейность оператор
![]() :
:
![]() ,
,
![]() ,
Следовательно
,
Следовательно
![]() -
первое условие не выполнено, а значит
не
является линейным оператором.
Для
оператора
-
первое условие не выполнено, а значит
не
является линейным оператором.
Для
оператора
![]() проверим
выполнение второго условия:
проверим
выполнение второго условия:
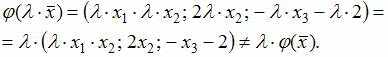 Условие
не выполняется, значит
не
линейный оператор.
Проверим выполнение
второго условия для оператора
Условие
не выполняется, значит
не
линейный оператор.
Проверим выполнение
второго условия для оператора
![]() :
:
![]() Следовательно,
данный оператор не является
линейным.
Проверим выполнение условий
линейности для оператора
Следовательно,
данный оператор не является
линейным.
Проверим выполнение условий
линейности для оператора
![]() :
:
![]() ,
,
![]() ,
Следовательно
,
Следовательно
![]() –
первое условие выполнено.
–
первое условие выполнено.
![]() –
второе условие выполнено. Поэтому
является
линейным оператором.
–
второе условие выполнено. Поэтому
является
линейным оператором.
Тема:
Основные алгебраические структуры
Подалгеброй
алгебры
![]() является
совокупность …
является
совокупность …
|
|
|
|
|
|
|
|
Решение:
Подалгеброй
алгебры
![]() ,
называют совокупность
,
называют совокупность
![]() ,
где
,
где
![]() ,
причем
,
причем
![]() замкнуто
относительно всех операций из
замкнуто
относительно всех операций из
![]() не
является подалгеброй алгебры
,
так как
не
является подалгеброй алгебры
,
так как
![]() и
не
являются подалгебрами алгебры
,
так как, не совпадают множества заданных
операций.
является
подалгеброй алгебры
,
так как
и
не
являются подалгебрами алгебры
,
так как, не совпадают множества заданных
операций.
является
подалгеброй алгебры
,
так как
![]() и
каждая главная операция является
ограничением соответствующей операции
на
и
каждая главная операция является
ограничением соответствующей операции
на
![]()
Тема:
Основные алгебраические структуры
![]() является
подалгеброй алгебры …
является
подалгеброй алгебры …
|
|
|
|
|
|
|
|
Решение:
является
подалгеброй алгебры
,
так как
![]() и
каждая главная операция является
ограничением соответствующей операции
на
и
каждая главная операция является
ограничением соответствующей операции
на
![]() .
.
Тема: Дробно-рациональные функции Разложение дробно-рациональной функции на элементарные дроби имеет вид
Тема:
Линейные отображения
Образом
вектора
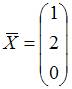 при
линейном преобразовании, заданном
матрицей
при
линейном преобразовании, заданном
матрицей
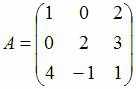 ,
является вектор …
,
является вектор …
|
|
|
|
|
|
|
|
Решение:
Так
как образ
![]() вектора
вектора
![]() определяется
по формуле:
определяется
по формуле:
![]() ,
то
,
то
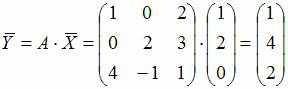 .
.
Тема: Основные алгебраические структуры Подалгеброй алгебры является совокупность …
|
|
|
|
|
|
|
|
Решение: Подалгеброй алгебры , называют совокупность , где , причем замкнуто относительно всех операций из не является подалгеброй алгебры , так как и не являются подалгебрами алгебры , так как, не совпадают множества заданных операций. является подалгеброй алгебры , так как и каждая главная операция является ограничением соответствующей операции на
Тема: Группы и подгруппы Мультипликативная группа рациональных чисел – это множество рациональных чисел …
|
без нуля с операцией умножения |
с операцией сложения |
|
с операцией умножения |
|
без нуля с отношением порядка |
|
Решение: Мультипликативная группа определяется операцией умножения. Поэтому множество рациональных чисел с операцией сложения и множество рациональных чисел без нуля с отношением порядка не являются мультипликативными группами. Множество рациональных чисел с операцией умножения не является группой, так как для элемента 0 нет обратного относительно умножения. Тогда мультипликативная группа рациональных чисел – это множество рациональных чисел без нуля с операцией умножения.
Тема:
Дробно-рациональные функции
Множество
всех дробно-рациональных функций
образует поле
относительно
обычных операций сложения и умножения
таких функций.
Пусть
и
,
причем
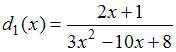 и
и
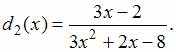 Тогда
числитель суммы
Тогда
числитель суммы
![]() равен
…
равен
…
|
|
|
|
|
|
|
|
Решение:
Разложим
на линейные множители знаменатели
дробно-рациональных функций
и
:
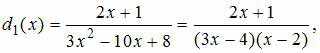
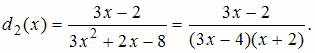 Тогда
Тогда
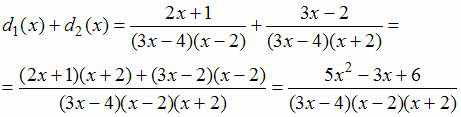 То
есть, числитель суммы
равен
.
То
есть, числитель суммы
равен
.
Тема:
Линейные отображения
Линейное
преобразование
![]() в
базисе
в
базисе
![]() имеет
матрицу
имеет
матрицу
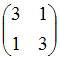 .
Тогда матрица этого оператора в базисе
.
Тогда матрица этого оператора в базисе
![]() ,
где
,
где
![]() ;
;
![]() ,
имеет вид …
,
имеет вид …
|
|
|
|
|
|
|
|
Решение:
Матрица
оператора
в
базисе
![]() вычисляется
по формуле
вычисляется
по формуле
![]() ,
где
,
где
![]() –
матрица перехода от базиса
к
базису
.
Матрица
перехода
–
матрица перехода от базиса
к
базису
.
Матрица
перехода
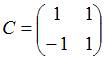 ,
тогда
,
тогда
 .
Матрица линейного оператора
.
Матрица линейного оператора
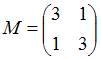 .
Тогда
.
Тогда
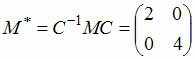 .
.
Тема: Группы и подгруппы Коммутативной группой является множество …
|
квадратных матриц с введенной операцией сложения |
невырожденных квадратных матриц с введенной операцией умножения |
|
натуральных чисел с 0, с введенной операцией сложения |
|
натуральных чисел с введенной операцией сложения |
|
Решение:
Множество
квадратных матриц с введенной операцией
сложения образует группу: ассоциативность
выполняется, нейтральным элементом
группы является нулевая матрица, для
любой матрицы существует
противоположная.
Множество невырожденных
квадратных матриц с введенной операцией
умножения образует группу, но она не
является коммутативной, т.к. не для любых
матриц
![]() и
и
![]() выполняется
равенство
выполняется
равенство
![]() .
Множество
натуральных чисел (с 0, или без него) с
введенной операцией сложения не является
группой, т.к. нет противоположного
элемента, например, у элемента
.
.
Множество
натуральных чисел (с 0, или без него) с
введенной операцией сложения не является
группой, т.к. нет противоположного
элемента, например, у элемента
.
Тема:
Основные алгебраические структуры
Для
кольца
![]() множество
множество
![]() ,
рассматриваемое с одной алгебраической
операцией сложения, представляет собой
…
,
рассматриваемое с одной алгебраической
операцией сложения, представляет собой
…
|
абелеву группу |
поле |
|
целостное кольцо |
|
область целостности |
|
Решение: Для кольца множество , рассматриваемое с одной алгебраической операцией сложения, представляет собой абелеву группу.
Тема:
Линейные отображения
Дано
линейное преобразование векторов на
плоскости
![]() ,
которое каждый вектор переводит в вектор
той же длины, но противоположно
направленный исходному. Тогда матрица
этого
преобразования имеет вид …
,
которое каждый вектор переводит в вектор
той же длины, но противоположно
направленный исходному. Тогда матрица
этого
преобразования имеет вид …
|
|
|
|
|
|
|
|
Решение:
Так
как
![]() и
и
![]() ,
то матрица такого линейного преобразования
имеет вид
,
то матрица такого линейного преобразования
имеет вид
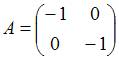 .
.
Тема: Основные алгебраические структуры В кольце квадратных матриц второго порядка единичный элемент …
|
– это матрица |
– это
матрица
|
|
– это
матрица
|
|
не существует |
|
Тема:
Дробно-рациональные функции
Даны
два полинома:
![]() и
и
![]() Тогда
целая часть от деления полинома
Тогда
целая часть от деления полинома
![]() на
полином
на
полином
![]() равна
…
равна
…
|
|
|
|
|
|
|
|
Решение:
Выполним
деление заданных полиномов
«уголком»:
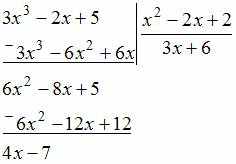 Тогда:
Тогда:
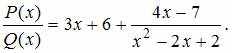 То
есть, целая часть от деления полинома
на
полином
равна
То
есть, целая часть от деления полинома
на
полином
равна
![]()
ема:
Основные алгебраические структуры
Элемент
![]() называется
обратным к элементу
называется
обратным к элементу
![]() в
группе G с единичным элементом
в
группе G с единичным элементом
![]() ,
если …
,
если …
|
|
|
|
|
|
|
|
Тема: Группы и подгруппы Подгруппой группы целых чисел с введенной операцией сложения является множество …
|
четных целых чисел |
нечетных целых чисел |
|
натуральных чисел |
|
натуральных чисел с нулем |
|
Решение: Данное подмножество должно быть замкнуто относительно операций сложения и взятия противоположного элемента. Этим условиям удовлетворяет, например, множество четных целых чисел.
Тема: Линейные отображения Линейным отображением пространства трехмерных векторов на пространство двумерных векторов является …
|
|
|
|
|
|
|
|
Решение:
Линейным
называется отображение
удовлетворяющее
условиям:
,
.
Проверим
на линейность отображение
:
![]() ,
,
![]() ,
Следовательно
–
первое условие не выполнено, а значит
не
является линейным отображением.
Для
отображения
проверим
выполнение второго условия:
,
Следовательно
–
первое условие не выполнено, а значит
не
является линейным отображением.
Для
отображения
проверим
выполнение второго условия:
![]() Условие
не выполняется, значит
не
линейное отображение.
Проверим
выполнение второго условия для отображения
:
Условие
не выполняется, значит
не
линейное отображение.
Проверим
выполнение второго условия для отображения
:
![]() Следовательно,
данное отображение не является
линейным.
Проверим выполнение условий
линейности для отображения
:
Следовательно,
данное отображение не является
линейным.
Проверим выполнение условий
линейности для отображения
:
![]() ,
,
![]() ,
Следовательно
–
первое условие выполнено.
,
Следовательно
–
первое условие выполнено.
![]() –
второе условие выполнено. Поэтому
является
линейным отображением.
–
второе условие выполнено. Поэтому
является
линейным отображением.
ДЕ2.Аналитическая геометрия
Тема:
Прямоугольные координаты на плоскости
Даны
три вершины параллелограмма:
![]() ,
,![]() ,
,
![]() .Тогда
четвертая вершина
.Тогда
четвертая вершина
![]() ,
противолежащая вершине В, имеет координаты
,
противолежащая вершине В, имеет координаты
![]() .
.
Решение:
Воспользуемся
формулой деления отрезка пополам.
Координаты точки
![]() ,
делящей отрезок между точками
,
делящей отрезок между точками![]() и
и
![]() пополам,
находятся по формулам:
пополам,
находятся по формулам:
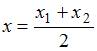 ,
,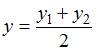 .
Найдем координаты точки М пересечения
диагоналей параллелограмма как координаты
середины отрезка АС (диагонали
параллелограмма точкой пересечения
делятся пополам):
.
Найдем координаты точки М пересечения
диагоналей параллелограмма как координаты
середины отрезка АС (диагонали
параллелограмма точкой пересечения
делятся пополам):
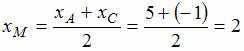 ,
,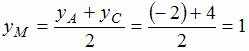 .
Зная координаты точек В и М (как середины
отрезка ВД) найдем координаты точки
.
Зная координаты точек В и М (как середины
отрезка ВД) найдем координаты точки
![]()
![]()
![]() то
есть точка имеет координаты
.
то
есть точка имеет координаты
.
Тема:
Прямая линия в пространстве
Острый
угол между прямыми и
и
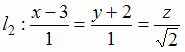 равен
равен
![]()
Решение:
Угол
между прямыми определяется как угол
между их направляющими векторами:
![]() и
и
![]() который
можно вычислить по формуле:
который
можно вычислить по формуле:
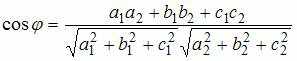 тогда
тогда
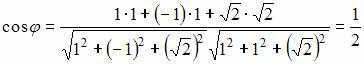
![]()
Тема:
Кривые второго порядка
Мнимая
полуось гиперболы
![]() равна
…
равна
…
|
|
|
3 |
Тема:
Плоскость в пространстве
Нормальное
уравнение плоскости
![]() имеет
вид …
имеет
вид …![]()
Тема:
Плоскость в пространстве
Плоскости
![]() и
и
![]() перпендикулярны
при значении
перпендикулярны
при значении
![]() ,
равном
,
равном
![]()
Решение:
Плоскости,
заданные общими уравнениями
![]() и
и
![]() перпендикулярны
при условии, что
перпендикулярны
при условии, что![]() .
Тогда
.
Тогда
![]() то
есть
.
то
есть
.
Тема:
Кривые второго порядка
Расстояние
между фокусами гиперболы
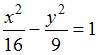 равно
10.
равно
10.
Тема:
Прямая линия в пространстве
Параметрические
уравнения прямой, параллельной оси
![]() и
проходящей через точку
и
проходящей через точку
![]() имеют
вид …
имеют
вид …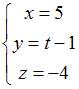
Решение:
Параметрические
уравнения прямой, проходящей через
точку![]() с
направляющим вектором
с
направляющим вектором![]() имеют
вид
имеют
вид
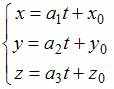 .За
направляющий вектор прямой можно взять
.За
направляющий вектор прямой можно взять
![]()
Тогда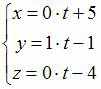 или
или
Тема:
Прямоугольные координаты на плоскости
Точка
![]() лежит
на оси абсцисс и равноудалена от точки
лежит
на оси абсцисс и равноудалена от точки
![]() и
начала координат. Тогда точка
и
начала координат. Тогда точка
![]() имеет
координаты …
имеет
координаты …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Так
как точка
лежит
на оси абсцисс, то ее ордината
![]() .
Так как точка
.
Так как точка
![]() равноудалена
от точки
и
начала координат
равноудалена
от точки
и
начала координат![]() , то расстояния от точки
до
точек
и
равны.
Тогда
, то расстояния от точки
до
точек
и
равны.
Тогда
![]() или
или
![]()
![]() ,
т.е.
,
т.е.
![]()
Тема:
Плоскость в пространстве
Общее
уравнение плоскости, проходящей через
точку
![]() перпендикулярно
прямой
перпендикулярно
прямой
![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Уравнение
плоскости, проходящей через точку
![]() с
нормальным вектором
с
нормальным вектором
![]() ,
имеет вид:
,
имеет вид:
![]() .
Так
как эта плоскость перпендикулярна
прямой
,
то в качестве нормального вектора
плоскости можно использовать направляющий
вектор этой прямой, то есть
.
Так
как эта плоскость перпендикулярна
прямой
,
то в качестве нормального вектора
плоскости можно использовать направляющий
вектор этой прямой, то есть
![]() .
Тогда
.
Тогда
![]() или
.
или
.
Тема:
Кривые второго порядка
Асимптоты
гиперболы
![]() задаются
уравнениями …
задаются
уравнениями …
|
|
|
|
Решение:
Асимптоты
гиперболы
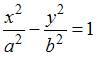 задаются
уравнениями вида
задаются
уравнениями вида
![]() .
Разделив обе части уравнения
на
36, получим каноническое уравнение
гиперболы:
.
Разделив обе части уравнения
на
36, получим каноническое уравнение
гиперболы:
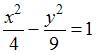 .
То есть
.
То есть
![]() и
и
![]() .
Тогда уравнения асимптот примут вид
.
.
Тогда уравнения асимптот примут вид
.
Тема:
Прямая линия в пространстве
Расстояние
между прямой
![]() и
плоскостью
и
плоскостью
![]() равно
…
равно
…
|
|
|
3 |
|
|
|
18 |
|
|
|
0 |
|
|
|
15 |
Решение:
Направляющий
вектор прямой имеет вид
![]() ,
а нормальный вектор плоскости:
,
а нормальный вектор плоскости:
![]() .
Скалярное произведение этих векторов
равно нулю:
.
Скалярное произведение этих векторов
равно нулю:
![]() .
Следовательно, прямая либо параллельна
плоскости, либо принадлежит ей. Тогда
расстояние между прямой и плоскостью
можно найти как расстояние между любой
точкой данной прямой и плоскостью. В
качестве такой точки возьмем, например,
.
Следовательно, прямая либо параллельна
плоскости, либо принадлежит ей. Тогда
расстояние между прямой и плоскостью
можно найти как расстояние между любой
точкой данной прямой и плоскостью. В
качестве такой точки возьмем, например,
![]() .
Расстояние от точки
.
Расстояние от точки
![]() до
плоскости
до
плоскости
![]() найдем
по формуле
найдем
по формуле
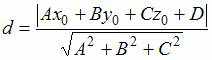 ,
то есть
,
то есть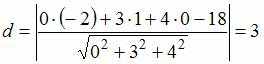
Тема:
Плоскость в пространстве
Уравнение
плоскости, проходящей через точки
![]() ,
,
![]() и
и
![]() ,
имеет вид …
,
имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Уравнение
плоскости, проходящей через точки
![]() ,
,
![]() и
и
![]() ,
не лежащие на одной прямой, имеет вид
,
не лежащие на одной прямой, имеет вид
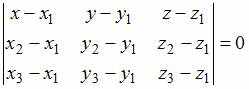 .
Подставим
числовые значения в полученное уравнение:
.
Подставим
числовые значения в полученное уравнение:
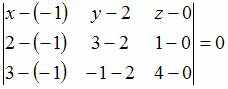 ,
или
,
или
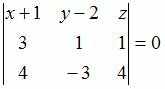 .
Раскрывая
определитель по первой строке, получим
.
Раскрывая
определитель по первой строке, получим
![]() ,
то
есть
,
то
есть
Тема:
Прямоугольные координаты на плоскости
Точки
![]() и
и
![]() лежат
на одной прямой, параллельной оси
ординат. Расстояние между точками
и
лежат
на одной прямой, параллельной оси
ординат. Расстояние между точками
и
![]() равно
6. Тогда положительные координаты точки
равны
…
равно
6. Тогда положительные координаты точки
равны
…
|
|
|
|
Тема:
Прямая линия в пространстве
Параметрические
уравнения прямой, параллельной оси
![]() и
проходящей через точку
имеют
вид …
и
проходящей через точку
имеют
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Параметрические уравнения прямой, проходящей через точку с направляющим вектором , имеют вид . За направляющий вектор прямой можно взять . Тогда или
Тема:
Прямоугольные координаты на плоскости
Точки
![]() ,
,
![]() и
и
![]() лежат
на одной прямой. Тогда точка
делит
отрезок
лежат
на одной прямой. Тогда точка
делит
отрезок
![]() в
отношении …
в
отношении …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Делением
отрезка
![]() в
заданном отношении
в
заданном отношении
![]() называется
поиск такой точки
на
отрезке
,
которая удовлетворяет соотношению
называется
поиск такой точки
на
отрезке
,
которая удовлетворяет соотношению
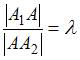 .
Тогда искомый параметр
будет
равен:
.
Тогда искомый параметр
будет
равен:
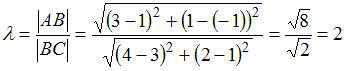
Тема:
Плоскость в пространстве
Общее
уравнение плоскости, проходящей через
точку
![]() параллельно
плоскости
параллельно
плоскости
![]() ,
имеет вид …
,
имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Уравнение
плоскости, параллельной плоскости
имеет
вид:
![]() .
Подставим координаты точки
в
это уравнение:
.
Подставим координаты точки
в
это уравнение:
![]() .
Тогда
.
Тогда
![]() .
.
Тема: Кривые второго порядка Мнимая полуось гиперболы равна … 3
Тема:
Плоскость в пространстве
Плоскости
и
перпендикулярны
при значении
![]() ,
равном …
,
равном …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Прямая линия в пространстве
Прямая
![]() параллельна
плоскости
параллельна
плоскости
![]() ,
если параметр
равен
…
,
если параметр
равен
…
|
|
|
– 11 |
|
|
|
– 7 |
|
|
|
7 |
|
|
|
11 |
Решение:
Прямая
параллельна плоскости, если скалярное
произведение направляющего вектора
прямой
![]() и
нормального вектора плоскости
и
нормального вектора плоскости
![]() равно
нулю. То есть
равно
нулю. То есть
![]() ,
или
,
или
![]() .
.
Тема: Прямоугольные координаты на плоскости Даны три вершины параллелограмма: , , . Тогда четвертая вершина , противолежащая вершине , имеет координаты …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Кривые второго порядка
Соотношение
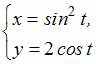 в
прямоугольной декартовой системе
координат задает …
в
прямоугольной декартовой системе
координат задает …
|
|
|
параболу |
|
|
|
гиперболу |
|
|
|
эллипс |
|
|
|
окружность |
Решение:
Вычислим
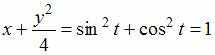 ,
то есть
,
то есть
![]() .
Тогда
в прямоугольной декартовой системе
координат данное уравнение задает
параболу с вершиной в точке
.
Тогда
в прямоугольной декартовой системе
координат данное уравнение задает
параболу с вершиной в точке
![]()
Тема:
Прямоугольные координаты на плоскости
В
треугольнике с вершинами
![]() ,
,
![]() и
и
![]() проведена
медиана
проведена
медиана
![]() ,
длина которой равна …
,
длина которой равна …
|
|
|
4 |
|
|
|
|
|
|
|
16 |
|
|
|
|
Решение:
Точка
является
серединой отрезка
![]() .
Координаты середины отрезка определяются
по формулам
.
Координаты середины отрезка определяются
по формулам
![]() ,
,
![]() .
Подставляя в эти формулы координаты
точек
и
,
получим координаты точки
:
.
Подставляя в эти формулы координаты
точек
и
,
получим координаты точки
:
![]() ,
,
![]() .
Расстояние между точками
и
можно
найти по формуле
.
Расстояние между точками
и
можно
найти по формуле
![]() .
То
есть
.
То
есть
![]()
Тема: Плоскость в пространстве Общее уравнение плоскости, проходящей через точку параллельно плоскости , имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Уравнение плоскости, параллельной плоскости имеет вид: . Подставим координаты точки в это уравнение: . Тогда .
Тема:
Кривые второго порядка
Фокусы
эллипса имеют координаты
![]() и
и
![]() ,
а его эксцентриситет равен 0,6. Тогда
каноническое уравнение эллипса имеет
вид …
,
а его эксцентриситет равен 0,6. Тогда
каноническое уравнение эллипса имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Каноническое
уравнение эллипса имеет вид
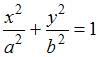 ;
фокусы эллипса имеют координаты
;
фокусы эллипса имеют координаты
![]() и
и
![]() ,
где
,
где
![]() ,
а эксцентриситет
,
а эксцентриситет
![]() .
Тогда
.
Тогда
![]() ,
,
![]() ,
,
![]() .
Следовательно,
получаем уравнение
.
Следовательно,
получаем уравнение
Тема: Плоскость в пространстве Общее уравнение плоскости, проходящей через точку перпендикулярно прямой , имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Уравнение плоскости, проходящей через точку с нормальным вектором , имеет вид: . Так как эта плоскость перпендикулярна прямой , то в качестве нормального вектора плоскости можно использовать направляющий вектор этой прямой, то есть . Тогда или .
Тема:
Прямоугольные координаты на плоскости
Даны
точки
![]() и
и
![]() .
Тогда координаты точки
.
Тогда координаты точки
![]() ,
симметричной точке
относительно
точки
,
равны …
,
симметричной точке
относительно
точки
,
равны …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Прямая линия в пространстве Параметрические уравнения прямой, параллельной оси и проходящей через точку имеют вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Параметрические уравнения прямой, проходящей через точку с направляющим вектором , имеют вид . За направляющий вектор прямой можно взять . Тогда или .
Тема:
Кривые второго порядка
Центр
окружности
![]() имеет
координаты …
имеет
координаты …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Окружность
радиуса
![]() с
центром в точке
с
центром в точке
![]() задается
на плоскости уравнением
задается
на плоскости уравнением
![]() .
Выделим в уравнении
полные
квадраты:
.
Выделим в уравнении
полные
квадраты:
![]() ,
или
,
или
![]() .
Тогда
центр окружности имеет координаты
.
Тогда
центр окружности имеет координаты
Тема:
Кривые второго порядка
Вершина
параболы
![]() имеет
координаты …
имеет
координаты …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Выделим
в уравнении
полный
квадрат:
![]() или
или
![]() .
Тогда вершина параболы имеет координаты
.
Тогда вершина параболы имеет координаты
ДЕ3.Дифференциальная геометрия