4. Примеры решения задач на обработку векторов

Задача 1.

Дан вектор Y, состоящий из n элементов. Составить программу-функцию, вычисляющую сумму элементов, для которых выполняется условие , и произведение положительных элементов вектора.

Задача 2.

В одномерном массиве Y, состоящем из n элементов. Составить программу-функцию, вычисляющую количество элементов, удовлетворяющих условию , и количество нулевых элементов вектора.

Задача 3. Дан вектор А, состоящий из 10 элементов. Составить программу-функцию, вычисляющую сумму элементов вектора А, расположенных между первым и последним отрицательными элементами.

5. Алгоритмы обработки матриц

Массивы, положение элементов в которых описывается двумя индексами, называются двуxмерными. Их можно представить в виде прямоугольной таблицы или матрицы. Для доступа к любому элементу матрицы нужно задать имя матрицы с дву­мя индексами. Первый индекс обозначает номер строки, второй — номер столб­ца. Рассмотрим алгоритмы обработки прямоугольной матрицы А размером .

Алгоритм суммирования элементов матрицы

Найти сумму нечетных элементов матрицы.

Алгоритм нахождения произведения элементов матрицы

Алгоритм подсчёта количества заданных элементов матрицы

Найти количество нулевых элементов матрицы.

А лгоритм нахождения минимального элемента матрицы и его индексов

А лгоритм суммирования элементов каждого столбца матрицы

Н айти сумму элементов первой и последней строки матрицы

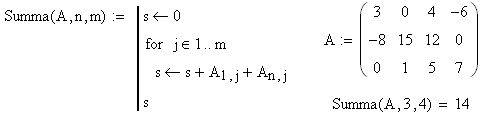
Найти сумму элементов первого и последнего столбца матрицы

П оиск максимального элемента в каждой строке матрицы

Алгоритмы обработки квадратных матриц

Сумма элементов главной диагонали

1 способ.

2 способ.

Сумма элементов в побочной диагонали

Сумма элементов, лежащих над главной диагональю

1 способ.

2 способ.

Сумма элементов, лежащих под главной диагональю

Сумма элементов, лежащих под главной диагональю, вычисляется аналогично суммированию элементов, лежащих над главной диагональю. Рассмотрим один из способов.

6. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ НА ОБРАБОТКУ МАТРИЦ

Задача 1. Дана матрица А размером . Составить программу-функцию, определяющую номера тех строк матрицы А, в которых второй элемент меньше среднего арифметического элементов этой строки.

Задача 2. Дана матрица Х размером . Составить программу-функцию, заменяющую нулями столбец, содержащий минимальный элемент главной диагонали.

6. ВЕКТОРНЫЕ И МАТРИЧНЫЕ ФУНКЦИИ

MATHCAD содержит ряд встроенных функций предназначенных для использования их с векторами и матрицами. Приведем некоторые векторные и матричные функции:

• lenght(V) возвращает число элементов в векторе V;

• last(V) возвращает индекс последнего элемента в векторе  V;

• max(V) возвращает максимальный элемент вектора V;

• min(V) возвращает минимальный элемент вектора V;

• sort(V) сортировка элементов векторов в порядке возрастания их значений;

• reverse(V) перестановка элементов (после sort) в обратном порядке;

• cols(M) возвращает число столбцов матрицы М;

• rows(M) возвращает число строк матрицы М;

• rank(M) возвращает ранг матрицы М;

• tr(M) возвращает след (сумму диагональных элементов) квадратной матрицы М;

• mean(M) возвращает среднее значение элементов массива М;

• median(M) возвращает медиану элементов массива М;

• csort (M, n) перестановка строк матрицы М таким образом, чтобы отсортированным оказался n-й столбец;

• rsort(M, n) перестановка строк матрицы М таким образом, чтобы отсортированной оказалась n-ая строка.

Рассмотрим применение этих функций при нумерации элементов массива по умолчанию начиная с нуля.