2.12 Силы, действующие в зацеплении

Окружная сила F_t1 = F_t2 =

Радиальная сила

где  угол профиля инструмента [2, c.24].

Осевая сила .

2.13 Проверка передачи на кратковременную пиковую нагрузку

Проверка выполняется при отсутствии в приводе предохранительных муфт и ременных передач.

Коэффициент перегрузки привода:

.

Максимальное контактное напряжение σ_{H max}

.

Максимальные напряжения изгиба

< [σ]_Fmax1;

< [σ]_Fmax2 .

2.14 Особенности расчета соосных редукторов

Межосевое расстояние редуктора определяется исходя из расчета на контактную выносливость тихоходной ступени (см. раздел 2.8.1). Для быстроходной ступени принимают то же межосевое расстояние и рассчитывается коэффициент ширины венца по межосевому расстоянию быстроходной ступени исходя из контактной прочности зубьев по формуле:

- для прямозубой передачи:

;

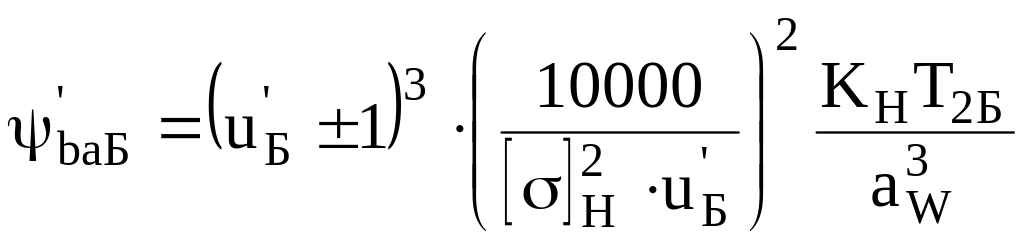• для косозубой и шевронной передачи:

.

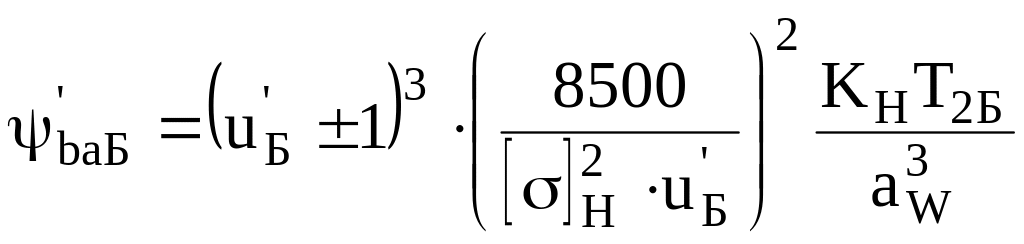Здесь - передаточное число быстроходной ступени;

- коэффициент нагрузки в быстроходной ступени, который следует принять =1,4÷1,6 (меньшие значения для легких режимов работы, а большие – для тяжелых режимов работы);

 момент на ведомом валу быстроходной ступени;

 допускаемое контактное напряжение для быстроходной ступени.

Если полученное значение получится меньше, чем 0,2, то его следует принять равным 0,2. Исключение составляют соосные передачи коробок скоростей (коробок подач) автомобилей, станков и другого оборудования, где коэффициент ширины венца можно принять также 0,1; 0,125 и 0,16.

Определение остальных параметров быстроходной ступени можно производить согласно разделов 2.12.13.

2. Особенности проектирования открытой цилиндрической зубчатой передачи

3.1 Общие положения

Поскольку открытые передачи работают, как правило, с малыми окружными скоростями (менее 1 м/с), то они выполняются прямозубыми, а коэффициент динамичности принимается равным единице. Для данных передач рекомендуется назначать 8-ю и 9-ю степени точности по нормам плавности согласно ГОСТ 1643-81. Такие передачи прирабатываются при любой твердости активных поверхностей зубьев, но изготавливают их в большинстве случаев из нормализованных или улучшенных сталей (см. таблицу 1). В процессе работы открытые передачи интенсивно изнашиваются, что и определяет особенности их расчета.

Исходные данные определяются аналогично п.2.1.

Выбор материала осуществляется согласно п.2.2, желательно применять нормализованные или улучшенные стали.

Определение суммарного N_∑ и эквивалентного чисел циклов перемены напряжений при расчете на изгибную выносливость производится аналогично п.2.4.2 и п.2.4.3, причем коэффициент приведения определяется по таблице 5 в зависимости от режима работы передачи.

Допускаемые напряжения изгиба и предельные допускаемые напряжения изгиба при расчете на кратковременную пиковую нагрузку определяются по формулам пп.2.5.2 и 2.6.2 для улучшенных и нормализованных сталей.

3.2 Проектный расчет открытой цилиндрической передачи

3.2.1 Числа зубьев колес и передаточное число

Число зубьев шестерни рекомендуется принимать Z₁ Z_min=17.

Число зубьев колеса Z₂=Z₁· , округлить до целого.

Фактическое передаточное число

3.2.2 Коэффициент ширины венца шестерни относительно делительного диаметра шестерни

Рекомендуется принимать при симметричном расположении шестерни относительно опор = 0,8 ÷ 1,4; при несимметричном  = 0,6 ÷ 1,2; при консольном  = 0,2 ÷ 0,4.

3.2.3 Коэффициент, учитывающий неравномерность распределения нагрузки по ширине зубчатого венца

Определяется по таблице 15 в зависимости от расположения шестерни относительно опор принятого значения и типа подшипников (опор) на которые опирается вал шестерни (шариковые или роликовые).

Таблица 15  Значения коэффициента в зависимости от и расположения колес относительно опор:

I – симметричное; II – несимметричное; III – консольное при установке на шарикоподшипниках; IV – консольное при установке на роликоподшипниках

	Расположение колес относительно опор
	I	II	III	IV
0,2	1,00	1,04	1,18	1,13
0,4	1,01	1,07	1,37	1,28
0,6	1,02	1,12	1,62	1,50
0,8	1,05	1,17	–	1,70
1,0	1,08	1,23	–	–
1,2	1,10	1,25	–	–
1,4	1,13	1,29	–	–
1,6	1,16	1,32	–	–

3.2.4 Коэффициенты, учитывающие форму зуба

Можно определять по формулам и (см. п. 2.10.1 и 2.10.2), либо по таблице 16 в зависимости от числа зубьев шестерни и колеса.

Таблица 16 – Значение коэффициента формы зуба

или	17	20	25	30	40	50	60	70	80	100 и более
или	4,28	4,09	3,90	3,80	3,70	3,66	3,62	3,61	3,61	3,60

3.2.5 Коэффициент , учитывающий уменьшение толщины зуба в его опасном сечении в последствии износа

Принимается по таблице 17.

Таблица 17 – Значения коэффициента

Износ в %	10	20	30
	1,25	1,50	2,00

3.2.6 Сравнительная оценка прочности зубьев на изгиб

Определяются отношения

и .

Дальнейший расчет ведется по параметрам звена, для которого вышеуказанные отношения принимают наименьшее значение. Обычно наименьшее отношение получается для параметров шестерни.

3.2.7 Предварительное значение модуля

.

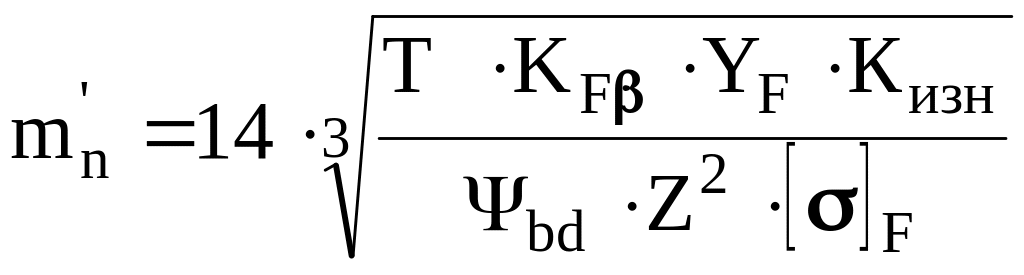Полученное значение модуля округляют до ближайшего значения по ГОСТ 9563-60 (см. п.2.8.3).

3.2.8 Рабочая ширина венца

Ширина шестерни

Ширина колеса

, мм.

Полученные значения округляют до ближайших по ГОСТ 6636-69 (см. п. 2.8.2).