6.Методические указания к самостоятельной работе студентов.

6.1.Линейная алгебра Определители и их вычисления

Матрицей размера mxn называется таблица, состоящая из m строк и n столбцов:

, (6.1.1)

где - элементы матрицы A, первый индекс i указывает на номер строки, а второй j на номер столбца, на пересечении которых находится элемент . В другой записи (1) имеет вид

. (6.1.2)

Если m=n, то матрица (1) называется квадратной.

Рассмотрим квадратную матрицу 2-го порядка

. (6.1.3)

Определителем 2-го порядка, соответствующим квадратной матрице (3), называется число, обозначаемое и определяющееся по следующему правилу:

. (6.1.4)

Пример6.1.1. .

Определителем 3-го порядка, соответствующим квадратной матрице A третьего порядка , (6.1.5)

называется число, обозначаемое и определяющееся по следующему правилу:

. (6.1.6)

Возьмем определитель 4-го порядка

(6.1.7)

и рассмотрим, например, его элемент . Мысленно зачеркнем третью строку и первый столбец, на пересечении которых находится этот элемент. Тем самым из оставшихся элементов образуем число

(6.1.8)

которое называется алгебраическим дополнением элемента . Определитель

, (6.1.9)

называется минором элемента . Таким образом, .

Определитель можно разложить по элементам любой строки или любого столбца.

Например, или .

Разложение удобно вести по строке (столбцу), где больше нулей.

Квадратная матрица A называется невырожденной (вырожденной), если ее определитель ( ).

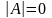Матрица называется обратной к матрице A, если , где E –единичная квадратная матрица.

. (6.1.10)

Квадратная матрица A имеет обратную тогда и только тогда, когда она не вырождена.

Матричный метод решения системы линейных алгебраических уравнений. Формулы Крамера. Метод Гаусса

Рассмотрим систему, составленную из трех линейных алгебраических уравнений с тремя неизвестными.

(6.1.11.)

Решением (2.1)называется система из трех чисел, удовлетворяющая требованию: если в (2.1) вместо и подставить соответственно и , то получим три верных равенства (три тождества).

(6.1.12)

- основная матрица системы (2.1)

(6.1.13)

- расширенная матрица (2.1)

; ; (6.1.14)

система (2.1) может быть записана в матричном виде так:

AX=D (6.1.15)

X – неизвестная матрица-столбец. Введем вспомогательные определители:

Предполагая, что матрица A - невырожденная и умножая (2.5) слева и почленно на A^-1, получим

–(6.1.16) матричный способ решения системы.

Используя понятие равенства двух матриц, получим

(6.1.17)

(6.1.18)

(6.1.19)

Элементарными преобразованиями матрицы называются следующие преобразования:

1. Перестановка местами произвольных двух строк (столбцов).

2. Умножение строки (столбца) на отличное от нуля число.

3. Прибавление к элементам строки (столбца) соответствующих элементов другой строки (столбца), предварительно умноженных на одно и то же число.

Пример 6. 1.2. Найти матрицу, обратную матрице . Проверить результат.

Обратную матрицу находим по формуле .

Вычислим определитель матрицы по правилу треугольника:

Определитель не равен нулю, следовательно, обратная матрица существует. Составляем матрицу из алгебраических дополнений ( ) и транспонируем ее.

;

;

;

;

;

;

;

;

;

.

Выполним проверку:

· =

.

·

Получим: A^-1A=AA^-1=E. Следовательно, обратная матрица найдена верно.

Ответ: .

Пример 6.1.3. Решить систему линейных уравнений по формулам Крамера

.

Решение:

Найдем главный определитель системы

Так как число уравнений и число неизвестных системы между собой равны m=n=3 и определитель отличен от нуля, система имеет единственное решение.

Найдем вспомогательные определители:

Неизвестные находим по формулам Крамера:

; .

Ответ: .

Пример 6.1.4.. Решить систему линейных уравнений методом Гаусса

.

Решение.

Метод Гаусса – это метод последовательного исключения неизвестных преобразованием данной системы линейных уравнений к эквивалентной. Преобразования уравнений системы заменяются преобразованием строк расширенной матрицы системы до приведения основной матрицы к треугольной или трапециевидной форме. Обнуление элементов выполняется элементарными преобразованиями матрицы(умножение строк на числа, отличные от нуля с последующим сложением).

.

Ответ: .

Пример 6.1.5. Применить теорему Кронекера – Капели и найти все решения системы методом Гаусса .

Решение.

Однородная матрица всегда имеет тривиальное решение, в данном случае (0;0;0;0), поэтому нас интересуют другие решения системы.

Применяем метод Гаусса:

.

Так как размерности основной и расширенной матриц системы 3x4 и 3x5 соответственно, ранги этих матриц не могут превышать числа 3. Попробуем посмотреть, есть ли для этих матриц минор третьего порядка, отличный от нуля. Составим его из первых двух и четвертого столбца: , так как определитель треугольного вида равен произведению элементов, стоящих на главной диагонали. Следовательно, ранги основной и расширенной матриц равны 3. По теореме Кронекера-Капелли данная система совместна. Так как число уравнений m=3 меньше числа неизвестных n=4, то она имеет бесчисленное множество решений. Закрепленных (базисных) переменных будет 3 (так как r=3), свободных переменных будет (n-r=4-3=1) одна. Минор, который мы составили выше, называется базисным, а переменные, входящие в него, базисными. Следовательно, - базисные переменные, а - свободная, то есть . Выполним обратный ход метода Гаусса:

.

Решением системы будет множество четверок чисел , где .

Например, (0;2;2;0), (0;-1;-1;0), - решения системы.

Ответ: .

Замечание. Обратите внимание, что тривиальное решение тоже задается этим множеством.

Пример 6. 1.6. Даны координаты векторов и в некотором базисе. Показать, что векторы образуют базис и найти координаты вектора в этом базисе.

; ; ; ; .

Решение.

Если векторы образуют базис, то существует разложение вектора в этом базисе , то есть

.

Отсюда вытекает решение задачи: найти координаты вектора в базисе означает решить систему четырех уравнений с четырьмя неизвестными . Эта система будет иметь единственное решение, если ее основной определитель будет отличен от нуля.

Решаем методом Гаусса:

Так как определитель треугольного вида равен произведению элементов, стоящих на главной диагонали , видим, что он отличен от нуля. Следовательно, векторы независимы и образуют базис.

Найдем координаты вектора b в этом базисе

.

Следовательно, или b=(5;0;-1;2) в базисе .

Ответ: .