
- •1. Цели и задачи дисциплины
- •2. Требования к уровню освоения содержания дисциплины
- •3.Трудоемкость дисциплины по видам занятий
- •4. Содержание дисциплины
- •4.1. Разделы дисциплины и виды занятий (в часах)
- •4.2. Содержание разделов
- •I семестр
- •Раздел 1. Элементы векторной алгебры и аналитической геометрии
- •Раздел 2. Введение в математический анализ: функция, теория пределов, непрерывность
- •Раздел 3. Дифференциальное исчисление функции одной переменной и его приложения
- •Раздел 4. Функции нескольких переменных
- •II семестр Раздел 5. Элементы теории функции комплексного переменного и высшей алгебры
- •Раздел 6. Неопределенный интеграл
- •Раздел 7. Определенный интеграл
- •Раздел 8. Кратные, криволинейные, поверхностные интегралы
- •III семестр
- •Раздел 9. Элементы теории поля
- •Раздел 10. Обыкновенные дифференциальные уравнения
- •5. Перечень практических занятий
- •I семестр
- •II семестр
- •III семестр
- •IV семестр
- •5 Самостоятельная работа студентов (срс)
- •6.Методические указания к самостоятельной работе студентов.
- •6.1.Линейная алгебра Определители и их вычисления
- •6.2.Аналитическая геометрия
- •Плоскость
- •Прямая в пространстве
- •Кривые второго порядка
- •6.3. Введение в математический анализ
- •Дифференциальные исчисления функций одной переменной
- •6.4. Дифференциальное исчисление функций нескольких переменных
- •6.5. Исследование функций на непрерывность
- •6.6. Неопределенные интегралы Многочлены. Теорема Безу
- •Неопределённый интеграл
- •Первообразная функция.
- •Свойства неопределённого интеграла.
- •Непосредственное интегрирование
- •Основные методы интегрирования
- •Основные методы интегрирования
- •Метод интегрирования по частям
- •Интегрирование некоторых функций, содержащих квадратный трехчлен
- •Универсальная подстановка
- •Вычисление интегралов вида
- •Интегрирование биноминального дифференциала.
- •Интегрирование рациональных дробей по методу Остроградского
- •6.7. Определенные интегралы Понятие определенного интнграла
- •Формула Ньютона-Лейбница
- •Вычисление площади Фигур
- •Площадь в полярных координатах
- •Вычисление объемов тел
- •Площадь поверхности вращения
- •Вычисление работы переменной силы
- •Вычисление центра тяжести плоской линии
- •Центр тяжести плоской фигуры
- •6.8. Криволинейные, кратные и поверхностные интегралы Объём цилиндрического тела. Двойные интегралы
- •Определение двойного интеграла
- •Теорема существования двойного интеграла
- •Свойства двойного интеграла
- •Теорема об оценке двойного интеграла
- •Замена переменных в двойном интеграле
- •Вычисление двойного интеграла в полярной системе координат
- •Тогда .
- •Решение
- •Поверхностные интегралы Определение поверхностного интеграла I рода
- •Поверхностные интегралы II рода
- •Вычисление поверхностного интеграла II рода
- •Формула Остроградского Связь между поверхностным интегралом и тройным интегралом
- •Связь поверхностного интеграла с криволинейным интегралом. Теорема Стокса
- •7.Контрольные работы
- •7.1.Контрольная работа №1
- •7.2.Контрольная работа №2
- •7.3. Контрольная работа №3
- •7.4.Контрольная работа №4
- •Задание 6. Вычислить криволинейный интеграл первого
- •Задание 8. Вычислить поверхностные интегралы второго рода
- •Задание 9 . Найти площадь поверхности
- •8. Учебно-методическое обеспечение дисциплины
- •9.Карта обеспеченности студентов учебниками, учебными пособиями, учебно-методическими материалами по дисциплине "Математика".
- •10. Перечень контрольных вопросов
- •Семестр II
- •Семестр III
- •Семестр IV
- •1.Цели и задачи дисциплины……………………….............1
Вычисление поверхностного интеграла II рода
Пусть гладкая поверхность S задана уравнением z = z (x,y) . Определена в замкнутой области G – проекции S на плоскость ОХУ . Рассмотрим на поверхности S
R(x,y,z) – непрерывная функция .
Разобьём S произвольно на n частей G1 , G2 , . . . ,Gn .
Выберем по произвольной точке Мi (i , i, i) .
Составим интегральную сумму :
=
 ,
,
где Si – площадь Gi , так как точка i = Z(i , i) .
Переходя в (4.1) к пределу при d0 получаем
 .
.
Аналогично :
.

G1 – проекция S на Oyz .

G2 – проекция S на Ozх .
Связь между поверхностными интегралами I и II рода
Пусть гладкая
ориентированая поверхность , на которой
задана непрерывная вектор – функция
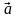 (М)
= [ P(x,y,z),
Q(x,y,z)
, R(x,y,z)]
,
(M)
– единичная нормаль = ( cos
, cos
, cos
) , тогда
(М)
= [ P(x,y,z),
Q(x,y,z)
, R(x,y,z)]
,
(M)
– единичная нормаль = ( cos
, cos
, cos
) , тогда
Отсюда видно , что если выбрать другую сторону поверхности , то направляющий косинус изменит знак .
Пример 6.8.11.Вычислить
 , где S
- поверхность треугольника , образованного
пересечением плоскости х – у +z
= 1 с координатными плоскостями : х = 0 ,
у = 0 , z = 0
в верхней стороне поверхности .
, где S
- поверхность треугольника , образованного
пересечением плоскости х – у +z
= 1 с координатными плоскостями : х = 0 ,
у = 0 , z = 0
в верхней стороне поверхности .





 .
.
Формула Остроградского Связь между поверхностным интегралом и тройным интегралом
ТеоремаЕсли функции P(x,y,z) , Q(x,y,z) , R(x,y,z)непрерывны вместе со своими частными производными I-го порядка в области V , ограниченной замкнутой поверхностью S , то имеет место формула
.
Пример 6.8.12.
 ,
,
где S – внешняя сторна сферы x2 + y2 + z2 = R2 .
Решение.
Применим формулу Остроградского :

Вводим сферические координаты
 .
.
Связь поверхностного интеграла с криволинейным интегралом. Теорема Стокса
Теорема Если Р(x,y,z) , Q(x,y,z) , R(x,y,z) есть непрерывные функции вместе со своими частными производными первого порядка на поверхности S, то имеет место формула
 ,
,
где L – граница поверхности S ;cos , cos , cos - направляющие косинусы нормали к поверхности S .
Пример 6.8.13.Вычислить
с помощью формулы Стокса
 ,
,
L-
окружность
А поверхностью S служит верхняя сторона полусферы x2 + y2 +z2 =1.



 .
.
![]()
7.Контрольные работы
7.1.Контрольная работа №1
Задание 1. Для матрицы третьего порядка вычислите ее определитель
и определитель матрицы, транспонированной к данной.
1.
 ; 2.
; 2.
 ; 3.
; 3.
 ;
;
4.
 ; 5.
; 5.
 ; 6.
; 6.
 ;
;
7.
 ; 8.
; 8.
 ;
9.
;
9.
 ;
;
10.
 ; 11.
; 11.
 ; 12.
; 12.
 ;
;
13.
 ; 14.
; 14.
 ; 15.
; 15.
 ;
;
16.
 ;
17.
;
17.
 ;
18.
;
18.
 ;
;
19.
 ; 20.
; 20.

Задание 2. Вычислите определитель четвертого порядка
1.
 ; 2.
; 2. ; 3.
; 3.
 ;
;
4.
 ; 5.
; 5.
 ; 6.
; 6.
 ;
;
7.
 ;
8.
;
8.
 ;
9.
;
9.
 ;
;
10.
 ; 11.
; 11.
 ;
12.
;
12.
 ;
;
13.
 ;
14.
;
14.
 ;
15.
;
15.
 ;
;
16.
 ;
17.
;
17.
 ;
;
18.
 ;
;
19.
 ;
20.
;
20.

Задание 3. Найдите матрицу, обратную матрице. Проверьте результат, вычислив произведение взаимно обратных матриц.
1.
 ; 2.
; 2.
 ;
;
3.
 ; 4.
; 4.
 ;
;
5.
 ; 6.
; 6.
 ;
;
7.
 ; 8.
; 8.
 ;
;
9.
 ; 10.
; 10.
 ;
;
11.
 ; 12.
; 12.
 ;
;
13.
 ; 14.
; 14.
 ;
;
15.
 ; 16.
; 16.
 ;
;
17.
 ; 18.
; 18.
 ;
;
19.
 ; 20.
; 20.

Задание 4. Решите систему линейных уравнений матричным способом.
1.
 ; 2.
; 2.
 ;
;
3.
 ; 4.
; 4.
 ;
;
5.
 ; 6.
; 6.
 ;
;
7.
 ; 8.
; 8.
 ;
;
9.
 ; 10.
; 10.
 ;
;
11.
 ; 12.
; 12.
 ;
;
13.
 ; 14.
; 14.
 ;
;
15.
 ;
16.
;
16.
 ;
;
17.
 ;
18.
;
18.
 ;
;
19.
 ; 20.
; 20.

Задание 5. Решите систему линейных уравнений по формулам
Крамера.
1.
 ;
2.
;
2.
 ;
;
3.
 ;
4.
;
4.
 ;
;
5.
 ;
6.
;
6. ;
;
7.
 ;
8 .
;
8 .
 ;
;
9.
 ;
10.
;
10.
 ;
;
11.
 ;
12.
;
12.
 ;
;
13.
 ;
14.
;
14.
 ;
;
15.
 ;
16.
;
16.
 ;
;
17.
 ;
18.
;
18.
 ;
;
19. ;
20.
;
20.

Задание 6. Найдите все решения однородной системы линейных уравнений методом Гаусса.
1. ; 2.
; 2. ;
;
3.
 ; 4.
; 4.
 ;
;
5.
 ; 6.
; 6.
 ;
;
7.
 ;
8.
;
8.
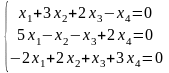 ;
;
9. ;
10.
;
10. ;
;
11. ; 12.
; 12. ;
;
13. ; 14.
; 14. ;
;
15. ; 16
; 16 ;
;
17. ; 18.
; 18. ;
;
19. ;
20.
;
20.
Задание 7. Даны координаты векторов а1, а2, а3, а4 и b в некотором базисе. Покажите, что векторы а1, а2, а3, а4 образуют базис и найдите координаты вектора b в этом базисе.
а1(1,2,-1,-2); а2(2,3,0,1); а3(1,2,1,3); а4(1,3,-1,0);b(7,14,-1,2).
а1(2,1,0,-1); а2(2,3,0,-2); а3(2,4,2,1); а4(0,-3,0,2);b(5,2,1,0).
а1(1,1,4,2); а2(2,-1,3,1); а3(0,2,0,0); а4(1,-1,0,1);b(5,0,0,5).
а1(1,2,3,4); а2(2,3,4,1); а3(3,4,1,2); а4(4,1,2,3);b(2,2,2,4).
а1(2,0,0,0); а2(0,4,0,0); а3(0,0,6,0); а4(0,0,0,8);b(6,7,0,1).
а1(1,2,-1,-2); а2(2,3,0,1); а3(1,2,1,3); а4(1,3,-1,0);b(6,7,0,1).
а1(2,3,4,5); а2(3,4,5,2); а3(4,5,2,3); а4(5,2,3,4);b(-1,2,1,-2).
а1(3,5,-1,-1); а2(3,5,1,4); а3(2,5,0,3); а4(1,3,-1,0);b(7,14,-1,2).
а1(4,4,0,-3); а2(4,7,2,-1); а3(2,1,2,3); а4(0,-3,0,2);b(5,2,1,0).
а1(3,0,7,3); а2(2,1,3,1); а3(1,1,0,1); а4(1,-1,0,1);b(5,0,0,5).
а1(3,5,7,5); а2(5,7,5,3); а3(7,5,3,5); а4(4,1,2,3);b(2,2,2,4).
а1(2,4,0,0); а2(0,4,6,0); а3(0,0,6,8); а4(0,0,0,8);b(-14,6,0,1).
а1(1,2,-1,-2); а2(3,5,-1,-1); а3(3,5,1,4); а4(2,5,0,3);b(6,7,0,1).
а1(2,1,0,-1); а2(4,4,0,-3); а3(2,7,2,-1); а4(2,1,2,3);b(-3,2,5,0).
а1(5,7,9,7); а2(7,9,7,5); а3(9,7,5,7); а4(5,2,3,4);b(-1,2,1,-2).
а1(1,3,5,3); а2(3,5,3,2); а3(5,3,1,3); а4(3,0,1,2);b(-6,0,2,-3).
а1(-1,1,3,1); а2(1,3,1,-1); а3(3,-1,-1,1); а4(2,-1,0,1);b(-3,6,7,-2).
а1(0,1,2,3); а2(1,2,3,0); а3(2,3,0,1); а4(3,0,1,2);b(-6,0,2,-3).
а1(-1,0,1,2); а2(0,1,2,-1); а3(1,2,-1,0); а4(2,-1,0,1);b(-3,6,7,-2).
а1(4,4,3,0); а2(-17,24,1,1); а3(-6,-1,2,0); а4(-5,3,1,0);b(-9,10,1,1).
Задание 8
По координатам вершин пирамиды а1 а2 а3 а4 найти:
1) длины ребер а1 а2 и а1 а3;
2) угол между ребрами а1 а2 и а1 аз;
3) площадь грани а1 а2 а3;
4) объем пирамиды а1 а2 а3 а4;
5) уравнения прямых а1 а2 иа1 а3;
6) уравнения плоской а1 а2 а3 иа1 а2 а4 ;
7) угол между плоскостями а1 а2 а3 иа1 а2 а4;
8) угол между ребром а1 а3 и гранью а1 а2 а4 ;
9) уравнение высоты, опущенной из вершины а4 на грань а1 а2 а3 ;
10) уравнение плоскости, проходящей через высоту пирамиды, опущенную из вершины а4 на грань а1 а2 а3 , и вершину а1 пирамиды ;
11) расстояние от вершины.а3до плоскости а1 а2 а4.
-
а1
а2
а3
а4
1
(3;1;4)
(-1;6;1)
(-1;1;6)
(0;4;-1)
2
(3;3;9)
(6;9;1)
(1;7;3)
(8;5;8)
3
(3;5;4)
(5;8;3)
(1;9;9)
(6;4;8)
4
(2;4;3)
(7;6;3)
(4;9;3)
(3;6;7)
5
(9;5;5)
(-3;7;1)
(5;7;8)
(6;9;2)
6
(0;7;1)
(4;1;5)
(4;6;3)
(3;9;8)
7
(5;5;4)
(3;8;4)
(3;5;10)
(5;8;2)
8
(6;1;1)
(4;6;6)
(4;2;0)
(1;2;6)
9
(7;5;3)
(9;4;4)
(4;5;7)
(7;9;6)
10
(6;6;2)
(5;4;7)
(2;4;7)
(7;3;0)
11
(0;3;2)
(-1;3;6)
(-2;4;2)
(0;5;4)
12
(-1;2;0)
(-2;2;4)
(-3;3;0)
(-1;4;2)
13
(2;2;3)
(1;2;7)
(0;3;3)
(2;4;5)
14
(0;-1;2)
(-1;-1;6)
(-2;0;2)
(0;1;4)
15
(3;0;2)
(2;0;6)
(1;1;2)
(3;2;4)
16
(0;2;-1)
(-1;2;3)
(-2;3;-1)
(0;4;1)
17
(2;3;2)
(1;3;6)
(0;4;2)
(2;5;4)
18
(-1;0;2)
(-2;0;6)
(-3;1;2)
(-1;2;4)
19
(2;0;3)
(1;0;7)
(0;1;3)
(2;2;5)
20
(2;-1;2)
(1;-1;6)
(0;0;2)
(2;1;4)
Задание 9
Составить общее уравнение плоскости, проходящей через точку М перпендикулярно плоскостям и :
-
M
1
(2;1;-5)
3X-2Y+Z+7=0
5X-4Y+3Z+1=0
2
(1;-1;1)
X-Y+Z-1=0
2X+Y+Z+1=0
3
(2;-1;1)
3X+2Y-Z+4=0
X+Y+Z-3=0
4
(1;8;2)
5X+6Y+11Z-3=0
3X+Y+4Z-12=0
5
(-1;-2;0)
4X+6Y-5Z-14=0
X+3Y-2Z-1 =0
6
(5;1;2)
X-7Y-2Z-10=0
2X-2Y-Z-13=0
7
(2;4;1)
X-2Y+5Z-7=0
2X-3Y+7Z-5=0
8
(1;1;1)
X-2Y+2Z+8=0
3X+5Y+7Z-1=0
9
(1;4;5)
X+Y+5Z+3=0
3X+2Y+8Z-9=0
10
(3;0;7)
X+Y+4Z=0
3X+2Y+7Z-2=0
Составить уравнение плоскости, проходящей через точки М1, М2 перпендикулярно плоскости :
-
М1
М2
11
(2;-1;4)
(3;2;1)
X+Y+Z-3=0
12
(1;1;1)
(2;2;2)
X-Y-Z=0
13
(0;-5;0)
(0;0;2)
X+5Y+2Z-10=0
14
(2;0;-1)
(1;-1;3)
3X+2Y-Z+3=0
15
(-1;-2;0)
(1;1;2)
X+2Y+2Z-4=0
16
(1;-2;4)
(2;-3;5)
X+Y-3Z+8=0
17
(0;1;3)
(1;2;7)
X+2Y+5Z+6=0
18
(1;1;0)
(2;-1;-1)
5X+2Y+3Z-7=0
19
(1;4;0)
(2;14;3)
X+6Y+Z-3=0
20
(9;1;1)
(19;2;2)
17X+2Y+Z+11=0
21
(7;1;0)
(26;2;3)
9X+Y+Z-17=0
22
(0;1;2)
(-1;2;3)
X+Y-Z+2=0
23
(3;4;6)
(5;1;5)
X+2Y+3Z-6=0
24
(4;1;0)
(2;-1;1)
X-Y+Z-3=0
25
(1;0;1)
(-1;1;0)
X+2Y-Z-1=0
Задание 10
Составить канонические уравнения прямой, заданной как линия пересечения двух плоскостей и :
-
1
x-2у+2z-8=0
x+2z-6=0
2
3x-5y+z-8=0
2x+y-z+2=0
3
x-2y+3z-4=0
3x+2y-5z-4=0
4
x+z-6=0
x+6y-4=0
5
x+2y-4=0
x-2y+2z-8=0
6
x+2Z-6=0
x+y+z-6=0
7
x+2y+3z-13=0
3x+y+4z-14=0
8
x+2y+3z-1=0
2x-3y+2z-9=0
9
2x+7y-z-8=0
Х+2y+z-4=0
Составить канонические уравнения прямой, проходящей через точку А параллельно прямой ℓ:
-
А
ℓ
10
(3;1;-1)
X+5y+2=0
3х+4y+2z-8=0
11
(2;0;-3)

12
(-4;3;0)
x-2y+z-4=0
2x+y-z=0
13
(2;-5;9)
2x-3y-3z-9=0
x-2y+3=0
Составить канонические уравнения прямой, проходящей через точку А перпендикулярно прямым ℓ1 и ℓ2:
-
А
ℓ1
ℓ2
14
(2;-3;4)


15
(0;1;1)


16
(2;-3;4)
x=t;y=t;z=2t+5
x=3t+8;y=2t-4;z=t+2
17
(0;1;-1)
x=3t+1;y=15t;z=7t-2
x=t;y=2t-5;z=6
18
(0;-1;1)
x=2t;y=t-5;z=3t-2
x=4t-1;y=4t+6;z=t-4
Составить канонические уравнения прямой, проходящей через точки а1 и а2:
|
а1 |
а2 |
19 |
(1;-2;1) |
(3;1;1)
|
20
|
(1;-2;1) |
(0;6;5)
|
21
|
(3;1;2) |
(0;2;5) |
22
|
(0;1;2) |
(5;2;1) |
23
|
(1;7;3) |
(0;2;1) |
24
|
(1;0;2) |
(5;1;4) |
25
|
(3;5;1) |
(2;3;1) |
Задание 11
Найти проекцию точки А на плоскости :
|
А |
|
1 |
(1;3;1)
|
x+2y+2z-30=0 |
2 |
(3;1;-1)
|
3x+y+z-20=0 |
3 |
(5;2;-1)
|
2x-y+3z+23=0 |
4 |
(4;-3;1)
|
x-2y-z-15=0 |
5 |
(1;-1;0)
|
5x-6y+2z-76=0 |
Найти точку, симметричную точке А относительно плоскости а:
|
А
|
а
|
6
|
(0;0;0;)
|
х-2у+4z-21=0
|
7
|
(1;5;2)
|
2х-у-z+11=0
|
8
|
(1;-3;-4)
|
Зх-у-2z=0
|
9 |
(5;2;-1)
|
2х-у+3z+23=0
|
10 |
(3;-4;-6) |
9х-7у-31z-108=0
|
Найти точку, симметричную точке А относительно прямой ℓ:
|
А |
ℓ |
11 |
(2;1;0) |
|
12 |
(4;3;10) |
|
13 |
(1;-1;2) |
|
14 |
(3;2;0) |
|
15 |
(2;-1;5) |
|
16 |
(0;0;0;)
|
|
Составить уравнения прямой, проходящей через точки пересечения плоскостиа с прямыми ℓ1 и ℓ2:
|
А |
ℓ1
|
ℓ2 |
17 |
2x+y-3z=0 |
|
|
18 |
3x-2y+z=0 |
|
|
19 |
6x+3y-41=0 |
|
|
20 |
3x-y-2z+5=0 |
|
|
21 |
2x+3y+z-1=0 |
|
|
Составить уравнения прямой, лежащей в плоскости и проходящей через точку пересечения плоскости с прямой ℓ, перпендикулярно вектору а:
|
|
ℓ |
_ а |
22 |
6x+3y-z-41=0 |
|
{1;2;1} |
23 |
x+2y=0 |
|
{3;-1;2} |
24 |
x+2y=0 |
|
{5;-1;2} |
25 |
3x-y-2z+5=0 |
|
{0;3;5} |
Задание 12
Составить общее уравнение плоскости, проходящей через параллельные прямые ℓ1 и ℓ2:
|
ℓ1 |
ℓ2 |
1 |
|
|
2 |
|
|
3 |
x=2t+1;y=-t;z=t+1 |
|
4 |
|
|
5 |
|
|
Составить общее уравнение плоскости, проходящей через прямую ℓ1, параллельно прямой ℓ2:
|
ℓ1 |
ℓ2 |
6 |
|
|
7 |
|
|
8 |
|
|
9 |
|
|
10 |
x=3t-1;y=-2t-3;z=-t+2
|
x=2t+2;y=3t-1;z=-5t+1 |
Составить общее уравнение плоскости, проходящей через точку М параллельно прямымℓ1 и ℓ2:
|
ℓ1 |
ℓ2 |
М |
11 |
|
|
(-2;0;0)
|
12 |
|
|
(6;1;1)
|
13 |
|
|
(1;2;1)
|
14 |
|
|
(1;2;3)
|
15 |
|
|
(0;0;2)
|
Составить общее уравнение плоскости, проходящей через пересекающиеся прямые ℓ1 и ℓ2:
|
ℓ1 |
ℓ2 |
16 |
|
|
17 |
x=z-2;y=2z+1
|
|
18 |
|
x=t+5;y=-4t-1;z=t-4 |
19 |
x=t+1;y=-2;z=-t+1
|
x=2t;y=2t-2;z=-3t+2 |
20 |
|
x=3t+7;y=2t+2;z=-2t+1 |
21 |
|
|
22 |
x=2t-3;y=3t-2;z=-4t+6
|
x=t+5;y=-4t-1;z=t-4 |
23 |
|
|
24 |
x=2t+1;y=3t-2;z=-6t+1
|
|
25 |
|
|

























































