Формула Ньютона-Лейбница

Если функция f(x) непрерывна на отрезке [a;b] иF(x)есть какая-либо первообразная для f(x) на этом отрезке, то справедлива следующая формула:

=F(b)-F(a) . (6.7.2)

Пример 6.7.1.. Вычислить: .

Решение: применим формулу Ньютона-Лейбница:

=F(x)| =F(b) - F(a)

Преобразуем подынтегральную функцию

.

Интегрирование по частям в определенном интеграле

Пусть функции U(x) и V(x) имеют непрерывные производные на [a;b], тогда справедлива формула

. (6.7.3)

Пример6.7.2. Вычислить: .

Решение: пусть , т. к. функции и непрерывны на вместе со своими производными, то согласно формуле (I) находим

.

Замена переменной в определенном интеграле

Пусть требуется вычислить , где f(x)- непрерывная на [a;b] функция. Часто здесь бывает удобно применить, как и в случае вычисления неопределенного интеграла, замену переменной путем введения вместо старой переменной новой переменной t, связанной со старой соотношением .

Итак, введем новую переменную t, положив .

Пусть выполняются следующие условия:

а) функция определена и непрерывна на отрезке ;

б) при изменении tна значения функции не выходят за пределы отрезка . При этом ;

в) Функция на отрезке имеет непрерывную производную .

Тогда имеет место равенство

(6.7.4)

При пользовании формулой (6.7.4) следует функцию стараться выбирать так, чтобы новый интеграл был более простым для вычисления, чем первоначальный.

Пример 6.7.3.Вычислить:

Решение: применим подстановку: . Найдем пределы интегралов для новой переменной при , при .

Следовательно, при применении x от1/3 до 1 новая переменная t изменяется от 3 до 1.

Функция - убывает и непрерывна вместе со своей производной

на отрезке

Пример 6.7.4. Вычислить: .

Решение.

Интегрирование в симметричных пределах четных и нечетных функций

При вычислении определенных интегралов от четных и нечетных функций полезно иметь в виду следующие формулы:

(в предположении, что f(x) – непрерывная на симметричном относительно начала координат отрезке [-a;a] функция).

Пример 6.7.5. Вычислить: .

Решение: подынтегральная функция чётная, поэтому

.

Интеграл от периодической функции по периоду

Пусть фуккция f(x) – непрерывная, периодическая с периодом Т, т.е. f(x+T)=f(x).

Для такой функции имеет место следующее свойство: интеграл от периодической функции по периоду не зависит от положения интервала интегрирования: , (т.е. на любом промежутке длины Тинтеграл от периодической функции имеет одно и то же значение).Пример Пример 6. Вычислить: .

Решение: подынтегральная функция имеет период T=π, поэтому из верхнего и нижнего периодов можно вычесть 2π, полученный интеграл будет равен данному:

Вычисление площади Фигур

Площадь в прямоугольных декартовых координатах Площадь криволинейной трапеции

П ри постановке задачи определенного интегрирования мы уже рассмотрели вопрос о вычислении площади криволинейной трапеции, т.е. фигуры, ограниченной прямыми x=a, x=b, y=0 и кривой y=f(x), гдеf(x) - неотрицательная, непрерывная на отрезке [a;b] функция , и установили, что площадь указанной фигуры вычисляется по формуле (рис. 1)

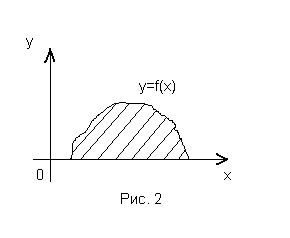
Если криволинейная трапеция ограничена .осью ОХ и другой кривой y= f(x), где f(x) - непрерывная, неотрицательная на данном отрезке функция, то для вычисления площади такой фигуры надо предварительно найти абсциссы точек пересечения кривой с осью OX, затем применить формулу (I) (рис. 2).

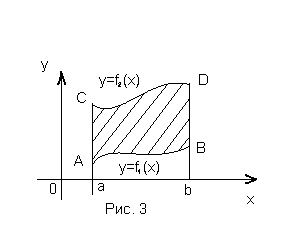
Если плоская фигура ограничена и снизу и сверху кривыми, уравнения которых y=f₁(x) и y=f₂(x), где a≤x≤b и функции f₁(x), f₂(x) – непрерывны причём f₁(x)≤ f₂(x), искомая площадь будет представлять собой разность площадей криволинейных трапеций aABb и aCDb:

или (рис. 3).

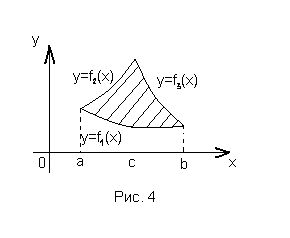
Пусть фигура ограничена сверху или

снизу дугами нескольких кривых. Для

вычисления площади такой фигуры стараются разбить эту фигуру на части прямыми, параллельными оси Оу, так , чтобы каждая часть была ограничена только одной кривой, как сверху, так и снизу.

( для случая, указанного на рис. 4).

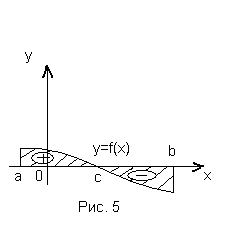
Если непрерывная на [a;b] функция f(x) меняет на нем знак так, что некоторые части графика данной функции находятся с одной стороны от оси ОХ, а иные - с другой, то для вычисления площади фигуры поступим следующим образом: в отдельности вычисляют площадь фигуры, расположенной выше оси ОХ, и фигуры ниже оси ОХ.

А затем берут сумму абсолютных величин всех полученных интегралов.

.

Пример 6.7.6.Вычислить площадь фигуры, ограниченной осью ОХ и синусоидой при 0≤х≤2π .

Площадь криволинейной трапеции, ограниченной кривой, заданной в параметрической форме

Пусть кривая, ограничивающая криволинейную трапецию сверху, задана уравнениями в параметрической форме: