Интегрирование некоторых функций, содержащих квадратный трехчлен

1)

.

а это - табличные интегралы.

2) коэффициенты действительного числа

в числителе выделяем производную знаменателя.

.

a,b,c – действительные числа

а) ; то имеем:

б) . В этом случае имеет смысл рассматривать только тогда, когда дискриминант трехчлена положителен:

Теперь имеем:

Замечание. На практике не пользуются обычно готовыми результатами, а предпочитают всякий раз проводить аналогичные вычисления вновь.

Пример.

4)

Преобразуем числитель так, чтобы из него можно было выделить производную квадратного трехчлена:

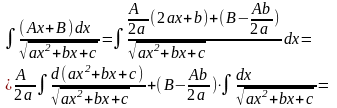
В связи с тем, что не существует на практике удобного общего метода вычисления неопределенных интегралов, приходится на ряду с частными методами интегрирования (см.предыдущую лекцию) рассматривать также способы интегрирования некоторых частных классов функций, интегралы от которых часто встречаются на практике.

Важнейшим классом среди них является класс рациональных функций.

«Интегрирование дробно-рациональных функций»

Интегрирование правильной рациональной дроби основано на разложении рациональной дроби в сумму элементарных дробей.

Элементарные (простейшие) дроби и их интегрирование.

Определение. Дроби вида: ; (1)

(2), где

(то есть корни трехчлена являются комплексными), называются элементарными.

Рассмотрим интегрирование элементарных дробей

1)

(при )

2)

(где пусть ).

Вычислим интеграл

(*)

Последний интеграл вычисляется с помощью рекуррентной формулы.

Иногда интегрирование по частям позволяет получить соотношение между неопределенным интегралом, содержащим степень некоторой функции, и аналогичным интегралом, но с меньшим показателем степени той же функции. Подобные соотношения называют рекуррентными формулами.

Обозначим через .

Имеем:

В последнем интеграле положим:

Поэтому

откуда

Таким образом, мы пришли к рекуррентной формуле: повторное применение которой в конечном счете приводит к «табличному» интегралу:

Затем вместо «t» и «k» подставляем их значения.

Пример6.6.26.

(по рекурр. формуле).=

.

Рациональной дробью называется функция представимая в виде ; где и - многочлены с действительными коэффициентами.

Рациональная дробь называется правильной если степень числителя меньше степени знаменателя.

Всякая правильная рациональная дробь может быть представлена в виде суммы конечного числа элементарных дробей.

Разложение правильной дроби на элементарные определяется следующей теоремой, которую рассмотрим без доказательства.

Теорема. Если дробь - правильная и , (где трехчлен не имеет действительных корней), то справедливо тождество:

(I)

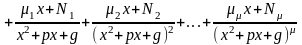;где

Отметим, что каждому действительному корню, например а, кратности « » многочлена в этом разложении соответствует сумма элементарных дробей вида (1), а каждой паре комплексно сопряженных корней и (таких, что ) кратности « » - сумма элементарных дробей вида (2).

Чтобы осуществлять разложение (I), нужно научиться определять коэффициенты .

Существуют различные способы их нахождения. Мы рассмотрим метод неопределенных коэффициентов и метод частных значений.

Метод неопределенных коэффициентов.

Равенство (I) есть тождество. Приведя его к целому виду, получим равенство 2-х многочленов. Но такое равенство всегда выполняется лишь при условии почленного равенства этих многочленов.

Приравнивая коэффициенты при одинаковых степенях х, стоящих в левой и правой частях равенства, получим систему линейных уравнений относительно неизвестных коэффициентов, которую надлежит решить.

Так как разложение (I) всегда существует для любой правильной рациональной дроби, то полученная система всегда совместна.

Такой метод нахождения коэффициентов называется методом неопределенных коэффициентов (способ сравнения коэффициентов).

Приведем пример разложения рациональной функции на элементарные дроби.

Пример 6.6.27. Разложить дробь на элементарные.

последнее уравнение подставим во второе

Таким образом, .

x=2 ;

x=3 .

Следует; .

Метод частных значений требует меньших затрат труда и поэтому заслуживает особого внимания при интегрировании рациональных дробей.

Если корни знаменателя только действительные, то для определения неизвестных коэффициентов целесообразно пользоваться именно этим способом.

В остальных случаях для определения неизвестных коэффициентов можно комбинировать оба способа.

Замечание. Метод частных значений применяется и тогда, когда другие случаи, но здесь нужно тождество дифференцировать.

Таким образом, для интегрирования правильных рациональных дробей достаточно уметь:

1. интегрировать элементарные дроби;

2. разлагать рациональные дроби на элементарные.

3. Интегрирование рациональных дробей

Схема интегрирования рациональных дробей:

Для интегрирования рациональных дробей ;

Где P(x) и Q(x) – многочлены с действительными коэффициентами, последовательно выполняют три шага.

Первый шаг. Если дробь неправильная, то есть степень числителя P(x) больше или равна степени знаменателя Q(x), выделяют целую часть рациональной дроби, деля числитель на знаменатель по правилу деления многочлена на многочлен. После этого рациональная дробь может быть записана в виде суммы:

1. выделенной целой части – многочлена М(х);

2. правильной остаточной дроби :

Второй шаг.

Правильную остаточную дробь разлагают на последующие дроби.

Для этого находят корни уравнения Q(x)=0 и разлагают знаменатель Q(x) на множители первой и второй степени с действительными коэффициентами:

В этом разложении знаменателя множители 1-й степени соответствуют действительным корням, а множители 2-й степени – параллельных сопряженных корней.

Коэффициент при большей степени х в знаменателе Q(x) можно считать равным 1 ибо этого всегда можно добиться, делением на него P(x) и Q(x).

После этого правильная остаточная дробь разлагается на простейшие (элементарные).

Третий шаг. Находят интегралы выделенной целой части и всех элементарных дробей (методами, рассмотренными выше), которые затем складывают.

Пример6.6.28.

Под знаком интеграла – неправильная рациональная дробь, так как степень числитель равна степени знаменателя, поэтому выделяем целую часть:

Таким образом:

x=0

x=2

x=3

Пример6.6.29.

Ответ: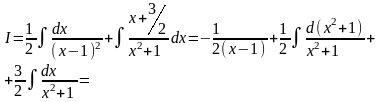

Пример 6.6.30.

Пример 6.6.31.

«Интегрирование некоторых классов тригонометрических функций»

Рассмотрим лишь некоторые классы тригонометрических функций, интегрируемых в конечном виде, для которых выработаны удобные на практике приемы интегрирования.