Непосредственное интегрирование

Метод непосредственного интегрирования является одним из простейших методов интегрирования.

Он опирается на:

1. таблицу интегралов;

2. основные свойства неопределенных интегралов.

Рассмотрим несколько примеров на применение метода непосредственного интегрирования:

Пример 6.6.8.Найти неопределенный интеграл

I = (использовать свойства 4 и 3; формулы 2,4а,6таблицы простейших интегралов.) = =

Проверка:

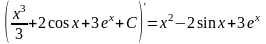
Пример 6.6.9.

.

Пример 6.6.10. .

Пример 6.6.11.

Прибавим и вычтем в числителе

В некоторых случаях сложное на первый взгляд выражение, стоящее под знаком интеграла, удается преобразовать и свести к простейшим формулам интегрирования:

Пример 6.6.12. .

Замечание. В таблице основных интегралов предполагалось, что х является независимой переменной.

Однако формулы этой таблицы остаются справедливыми и в случае, когда ; где - любая дифференцируемая функция новой переменной t.

Доказано, пусть (*) , ,и пусть 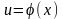дифференцируемая функция х.

В силу инвариантности формы первого дифференциала

, откуда (**)

Итак, из справедливости формулы (*) следует справедливость формулы (**), которая получается из первой формулы формальной заменой х на U.

На основании этого свойства получаем обобщенную таблицу простейших интегралов.

,

и т. д., где u – любая дифференцируемая функция х.

Примеры 6.6.12.

1) ;

2) ;

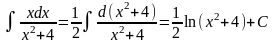3) ;

Основные методы интегрирования

К наиболее важным методам интегрирования относятся:

1. метод непосредственного интегрирования (с которым мы познакомились в предыдущей лекции);

2. метод замены переменной;

3. метод интегрирования по частям.

Метод замены переменной (или метод подстановки)

Этот метод основан на следующей теореме:

Теорема. Если F(x)- первообразная функции f(x), а - дифференцируемая функция, то функция также имеет первообразную, причем

Поскольку - формула замены переменной в неопределенном интеграле.

Таким образом, метод замены переменной состоит в следующем:

Пусть требуется вычислить , причем непосредственно подобрать первообразную для функции нельзя, но известно, что она существует.

Введем в место х новую переменную t, положив ,

где -дифференцируемая функция.

Тогда

Допустим, что интеграл, стоящий в первой части равенства, легко находится:

Итак, метод подстановок заключается в том, что в данном интеграле переменную х заменяют некоторой функцией от новой переменной t.

Это приводит к новому интегралу , более простому при удачном выборе функции .

После его вычисления в полученном результате заменяют «t» через «x».

Этим самым будет найден интеграл .

Пример6.6.13.

положим ,чтобы все корни извлекались .

Пример 6.6.14.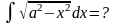

.

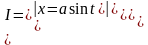
Обязательно возвращаться к исходной переменной х.

При замене переменной очень часто удобно бывает задавать не х как функцию от t, а, наоборот, задавать t как функцию от x и писать подстановку в виде

Теоретически оба эти способа равнозначны.

Рассмотрим ряд примеров на применение подстановки .

Пример 6.6.15.

.

Пример 6.6.16. .

Пример 6.6.17. .

В последних двух примерах иногда интегрирование целесообразно выполнять без формального введения новой переменной (новой буквы) – применить способ подведения под знак дифференциала.

Доказано, по определению дифференциала функции, .Переход в этом равенстве слева направо называют «подведением множителя под знак дифференциала».

Если под интегральное выражение может быть разбито на 2 множителя, один из которых есть дифференциал некоторой функции , а другой представляет собой легко интегрируемую функцию от t:

, то целесообразно подстановку производить устно, в уме, это освобождает от излишней записи и ускоряет операцию интегрирования.

Так, в рассмотренных выше примерах это будет выглядеть таким образом.

Пример6.6.18. .

Пример 6.6.19. .

Пример 6.6.20. .

Заметив, что подведем под знак дифференциала