6.5. Исследование функций на непрерывность

Пример6.5.1.

Найти точки разрыва функции и исследовать их характер:

а) у = 1/(х + 3); б) у =1/(1 + 2^1/х).

Построить схематично график функций в окрестности точек разрыва.

При решении примеров такого рода следует проверить выполнение условия непрерывности функции в точке

а) Функция у = 1/(х + 3) определена при всех значениях х, кроме х = -3. Так как это функция является элементарной, то она непрерывна в каждой точке своей области определения, состоящей из двух промежутков: (–

Следовательно, единственно возможной точкой разрыва является точка х = – 3. Функция определена в окрестности этой точки, в самой же точке нарушается условие непрерывности – функция в ней не определена. Для исследования характера разрыва найдем левый и правый пределы этой функции при стремлении аргумента к точке х = –3.

Следовательно, при х = –3 функция у = 1/(х + 3) имеет бесконечный разрыв, т.е.

y

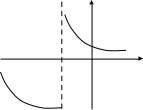
-3

0

x

точка х = –3 есть точка разрыва 2 рода.

б) Рассуждая аналогично, получим, что возможной точкой разрыва функции является х = 0. Найдем односторонние пределы этой функции в точке х = 0:

y

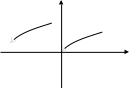
0

x

Таким образом, левый и правый пределы исследуемой функции при х = 0 конечны.

Поэтому х = 0 – точка скачка функции, разрыв I рода.

6.6. Неопределенные интегралы Многочлены. Теорема Безу

Многочленом n-й степени наз-ся функция вида:

где 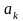- постоянные коэф-ты (действительные или комплексные), Z – переменная, вообще говоря, комплексная (Z=x+iy).

Определение. Числоа наз-ся корнем или нулём многочлена , если

Теорема Безу. Для того чтобы многочлен имеем (комплексный) корень ,необходимо и достаточно, чтобы он делился на , т.е. чтобы его можно было представить в виде произведения где - некоторые многочлены степени n-1.

Неопределённый интеграл

Как известно, основной задачей дифференциального исчисления функции одной переменной является отыскание производной , или, иными словами, дифференцирование данной функции .

К вопросу отыскание производной приводит ряд задач математики и её приложений кфизики практике.

Пример 6.6.1.

Решая задачу об отыскании скорости V, которую имеем в данный момент t точка, движущаяся по закону: мы сводим этот вопрос к отысканию производной: так что скорость v есть производная от пути до времени.

Но часто встречается необходимость в решении задачи, обратной задаче о дифференцировании функции.

Задача состоит в следующем:

Дана функция , являющаяся производной некоторой функции ; требуется найти функцию .

(это и есть основная задача интегрального исчисления)

К такой математической задаче приводят многие физические, химические и другие задачи.

Например:

1. Задача о разыскании закона неравномерного движения материальной точки вдоль прямой по заданной скорости;

2. Задача о нахождении закона химической реакции по известной её скорости.