21. Дифференцируемость функции в точке. Условия дифференцируемости функции в точке.

Определение. Функция y=f(x) называется дифференцируемой в точке x0, если ее приращение Δy в точке x0 может быть представлено в виде: Δy=A•Δx+α(Δx)•Δx, где A•Δx – линейная часть приращения, а α(Δx) - бесконечно малая функция от переменной Δx, т.е. limα(Δx)=0 при Δx→0.

Теорема. Для того, чтобы функция y=f(x) была дифференцируема в точке x0, необходимо и достаточно, чтобы она в этой точке имела конечную производную, причем A=f ‘ (x0).

Доказательство

Необходимость. Предположим: функция дифференцируема в точке x0, т.е. Δy=A•Δx+α(Δx)•Δx. Разделив обе части данного равенства на Δx, получим: Δy/Δx=A+α(Δx).

Достаточность. Пусть существует конечная производная y`(x0)∈R . Покажем дифференцируемость функции y`(x0)=lim (Δy/Δx) при Δx→0.

Если функция f(x) имеет конечный предел b при Δx→0 , то ее можно представить: f(x)=b+α(x) (α(x)→0) . Исходя из этого: Δy/Δx =y/(x0)+α(Δx), где limα(Δx)=0 при Δx→0, y/(x0) = Δy/Δx–α(Δx)→ A=y/(x0) . Теорема доказана.

22. Дифференцируемость и непрерывность.

Теорема о связи дифференцируемости и непрерывности.

Если функция y=y(x) дифференцируема в точке x0, то она и непрерывна в этой точке. Справедливость утверждения следует из Δy=y/(x0)·Δx+α(Δx)·Δx и limΔx→0Δy=0, а по определению функция непрерывна, если малому приращению аргумента соответствует малое приращение функции.

Обратное утверждение не верно.

Например, функция y=∣x∣  непрерывна в точкеx=0, но не дифференцируема в этой точке. Таким образом, не всякая непрерывная функция дифференцируема, а любая дифференцируемая функция непрерывна.

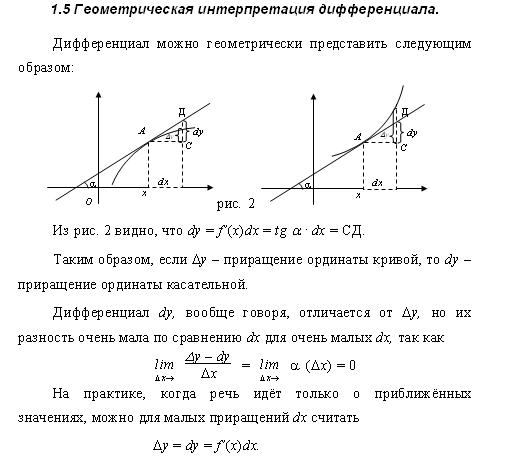
23. Дифференциал. Геометрическая интерпретация дифференциала.

Определение. Дифференциалом функции y=f(x) в точке x0 называется главная линейная относительно Δx часть приращения функции Δy в данной точке. y`=dy/dx.