15. Сравнение бесконечно малых.

Отношение бесконечно малых величин образует так называемую неопределенность .

Определения

Допустим, есть бесконечно малые при одном и том же  величины α(x) и β(x).

• Если 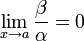 , то β — бесконечно малая высшего порядка малости, чем α. Обозначают β = o(α).

• Если 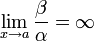 , то α — бесконечно малая высшего порядка малости, чем α. Соответственно, α = o(β).

• Если 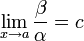  (предел конечен и не равен 0), то α и β являются бесконечно малыми величинами одного порядка малости. Они эквивалентны, если с = 1. Это обозначается как β = O(α) или α = O(β) (в силу симметричности данного отношения).

• Если 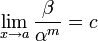  (предел конечен и не равен 0), то бесконечно малая величина β имеет m-й порядок малости относительно бесконечно малой α.

• Теорема.

┘ α(х) ~ α₁(x), а β(х) ~ β₁(x) тогда

=

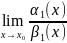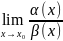
Доказательство.

= =

17. Свойства непрерывных в точке функций.

Функция f(x₀), определенная в окрестности некоторой точки х₀, называется непрерывной в точке х₀, если предел функции и ее значение в этой точке равны, т.е.

Свойства:1) Сумма, разность и произведение непрерывных в точке х₀ функций – есть функция, непрерывная в точке х₀.( h₁(x)=f(x) + g(x), h₂(x)=f(x)- g(x), h₃(x)=f(x)* g(x)).

Данное утверждение верно следуя теоремам:

1.Пусть функции f(x) и g(x) имеют пределы при одной и той же базе  :

Тогда функция h(x)=f(x) + g(x) также имеет предел при базе , и этот предел равен сумме пределов слагаемых.

2. Пусть функции f(x и g(x) имеют пределы при одной и той же базе  :

Тогда функция h(x)=f(x) + g(x) также имеет предел при базе , и этот предел равен произведению пределов сомножителей:

2) Частное двух непрерывных функций – есть непрерывная функция при условии, что g(x) не равна нулю в точке х₀.

Данное утверждение верно следуя теореме:

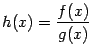Пусть при одной и той же базе существуют пределы и , причём . Тогда функция определена на некотором окончании базы , существует предел , и 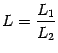, то есть предел отношения равен отношению пределов числителя и знаменателя.

3) Суперпозиция непрерывных функций – есть непрерывная функция.

Это свойство может быть записано следующим образом:

Если u = f(x), v = g(x) – непрерывные функции в точке х = х₀, то функция v = g(f(x)) – тоже непрерывнаяфункция в этой точке.

Данное утверждение верно следуя следствию к теореме о произведении представленную выше:

Пусть функции имеют при базе пределы, равные соответственно , и  -- постоянные. Тогда

20. Теорема о промежуточных значениях непрерывной на отрезке функции.

Она же теорема Больцана-Коши

Пусть F(x) непрерывна на отрезке [a, b], F(a)=A, F(b)=B, A≠B и C – некоторое число, находящееся между A и B, тогда существует такое число c  [a ,b], что F(c)=C (причём число C достигается только если c  [a ,b] ).

Доказательство

Пусть A<B и A<C<B. Разделим [a, b] срединной точкой на 2 части и выберем ту часть [a1, b1], что F(a1)<C< F(b1) (т.е. тот, в котором оказалась точка С). Затем разделим и этот отрезок и т.д. Получим систему стягивающихся последовательностей [a, b]ɔ [a1,b1]ɔ … ɔ[an, bn] , притом длина стремится к нулю. Для такой системы существует единственная точка ε такая, что ε принадлежит [an, bn] , n є N, причём Lim(x->∞)an = Lim(x->∞)bn =ξ. Значит F(ξ) = C. По теореме о сжатой переменной C-> F(ξ), следовательно F(ξ)=С.