10. Предел функции в точке (определения). Односторонние пределы.

а. Односторонние пределы.

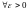
Определение. Число A называется левосторонним пределом функции в точке (пределом при , стремящемся к слева), если : выполнено неравенство |f(x) – a|< ε. Обозначение: f(x) (или .

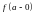Аналогично дается определение правостороннего предела функции (или f(b+0)).

Пример.

b. Предел функции по Гейне

Значение называется пределом функции в точке если для любого наперёд взятого положительного числа найдётся отвечающее ему положительное число такое, что для всех аргументов

удовлетворяющих условию выполняется неравенство .

Предел функции по Коши

Значение называется пределом функции в точке , если для любого наперёд взятого положительного числа найдётся отвечающее ему положительное число такое, что для всех аргументов , удовлетворяющих условию , выполняется неравенство .

Окрестностное определение по Коши

Значение называется пределом функции в точке , если для любой окрестности точки существует выколотая окрестность точки такая, что образ этой окрестности лежит в .

Вопрос №11 Свойства функций, имеющих предел

Пусть 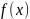определена в

Свойство №1

Пусть имеет конечный предел в точке ограничена в некоторой окрестности этой точки .

Арифметические свойства функции, имеющей предел

Свойство №2

Пусть 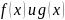имеют конечные пределы А и В соответственно в точке также имеют пределы в точке , равные соответственно .

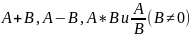Свойство №3

Пусть определены в , и в ней выполняется 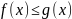и пусть .

Свойство №4(Теорема о сжатой переменной)

Пусть 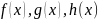определены в некоторой , в ней выполняется и пусть .

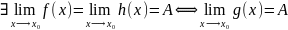13. Второй замечательный предел.

Доказательство второго замечательного предела:

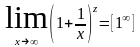
Два случая:

1. X>0

;

.

Если , то .

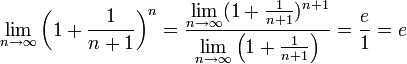
, Ч.Т.Д.

2. Х<0. Пусть x= - t.

, Ч.Т.Д.

Если = t, то = e // вторая формулировка второго замечательного предела.

14. Бесконечно малые и бесконечно большие функции. Свойства бесконечно малых.

Определение 1 (Бесконечно малая). α(х) называется бесконечно малой в точке х , если lim α(х)=0, где х стремится к х Определение 2 (Бесконечно большая). f(х) называется бесконечно большой в точке х , если lim f(х)=∞, где х стремится к х Свойства бесконечно малых. Свойство 1 Алгебраическая сумма любого конечного числа бесконечно малых является бесконечно малой. 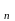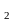Доказательство: Пусть α (х) …α (х) – бесконечно малые в точке х lim(α (х) + α (х) +…+ α (х)) = 0 (х стремится к 0) Свойство 2 Произведение бесконечно малой в точке х на ограниченную в некоторой окрестности х функцию этой точки функции f(х) является бесконечно малой. Доказательство: Пусть α(х) – бесконечно малая в точке х , β(х) – определена в некоторой окрестности х .

Тогда существует М >0, такое, что в некоторой окрестности этой точки выполняется неравенство │β(х)│ ≤ М │α(х) × β(х)│ = │α(х)│ × │β(х)│ < ε/М × М = ε

< ε/М ≤ М