1. Ограниченные числовые множества. Теорема о существовании точной верхней и точной нижней грани.

а. Числовое множество D называется ограниченным сверху, если M R, такое, что

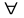x D: x≤M. M в этом случае называется точной верхней гранью.

б. Числовое множество D называется ограниченным снизу, если существует такое малое m из R, что x D: x≥m. M в этом случае называется точной нижней гранью.

в. Если множество D ограничено сверху и снизу, оно называется ограниченным, т.е. m,M R и m<M, что для x D: m≤x≤M.

в. Множество D называется ограниченным, если а>0, что для x D: |x|≤a (если все элементы множества по модулю не превосходят заданное a, то оно ограничено).

г. Множество D называется неограниченным, если для любого сколь угодно большого числа A > 0 найдется элемент x ∈ D , удовлетворяющий неравенству: x ≥ A .

д. Наименьшая из верхних граней множества D называется точной верхней гранью.

= sup D (супремум)

д. Число М называется точной высшей гранью множества D, если

1. x≤ для х D //x - переменная

2. ε>0 D: > - ε // – число

е. Наибольшая из нижних граней множества называется точной нижней гранью.

- inf D (инфимум)

е’. называется точной нижней гранью множества D, если выполняется

1) x ≥ для x D

2) ε>0 D: < + ε

Теорема о существовании точной верхней и точной нижней грани. Если непустое множество ограничено, оно имеет точную нижнюю и точную верхнюю грани.

2.Предел последовательности. Свойства сходящихся последовательностей, выражаемые равенствами.

Предел последовательности – число а такое, что для любого ε>0 существует N такое, что для любого n≥N: |x_n – a|< ε, a= x_n.

Если а – конкретное число, то последовательность сходящаяся, иначе - расходящаяся.

Свойства сходящихся последовательностей.

Свойство 1: Предел сходящейся последовательности единственен.

Свойство 2: Если последовательность {x_n}-сходящаяся, то она ограничена.

Доказательство.

Пусть последовательность {x_n} сходящаяся, a= x_n , ε>0 и существует N такое, что для любого n≥N: |x_n – a|< ε. Начиная с x_N, все x попадают в окрестность точки 0 с радиусом ε. За пределами окрестности может быть определенное количество членов последовательности, а это означает, что возможно поместить всю последовательность в некий отрезок AB, что в свою очередь означает, что последовательность ограничена.

Но обратное утверждение не имеет места.

Свойство 3: Арифметические свойства сходящихся последовательностей.

Пусть {x_n}, {y_n}-последовательности, сходящиеся соответственно к а и b. То есть

a= x_n, b= y_n, следовательно, { x_n± y_n}, { x_n * y_n}, { } являются сходящимися последовательностями, причем

{ x_n± y_n}= a±b;

{ x_n * y_n}= a * b;

= , b 0.

Доказательство.

Пусть a= x_n, b= y_n

|(xn+yn)-(a+b)|=|(xn-a)+(yn-b)|

|(xn-a)+(yn-b)| |xn-a|+|yn-b| , значит

{ x_n± y_n}= a±b

Но обратное утверждение не имеет места.

4. Монотонные последовательности. Сходимость монотонных последовательностей.

О1.{Xn} - называется неубывающей, если для любого n <=

О2.{Xn} - называется строго возрастающей, если для любого n <

О3.{Xn} - называется невозрастающей, если для любого n =>

О4.{Xn} - называется строго убывающей, если для любого n >

О1 и О2 - возрастающие последовательности

О3 и О4 - убывающие последовательности

Теорема: Пусть {Xn} – монотонная и ограниченная, следовательно {Xn} – сходится

Доказательство: Пусть {Xn} возрастающая и ограниченная сверху. Докажем, что она сходится.

{Xn} ограничена сверху, поэтому имеет точную верхнюю грань по известной теореме (Числовое множество D называется ограниченным сверху, если M R, такое, что x D: x≤M) М = sup{Xn} Докажем, что М и есть предел последовательности.

Докажем, что М = Lim {Xn} при n ;

n такое, что |M–x_n| < ε, ч.т.д.

Аналогично можно доказать, что если последовательность убывающая и ограничена снизу, то она тоже сходится.