2. Параметрические методы сравнения двух выборок. Сравнение дисперсий. Критерий t-Стьюдента для зависимых и независимых выборок.

Одной из распространенной задач количественной обработки в психологии является задача проверки значимости различия двух средних значений разных статистических совокупностей. Иначе говоря, являются ли рассматриваемые выборки представителями разных генеральных совокупностей? Существенны ли количественные различия средних значений и правомерны ли выводимые отсюда различия сугубо качественные?

Критерий Стьюдента (Госсета) предполагает нормальные распределения в выборках, различия средних значений которых проверяются на статистическую значимость. Этот критерий основан как бы на оценке общих частей двух статистических совокупностей (см.рис. 1), т.е. включает в себя “измерение” и разницы средних значений и мер их разброса.

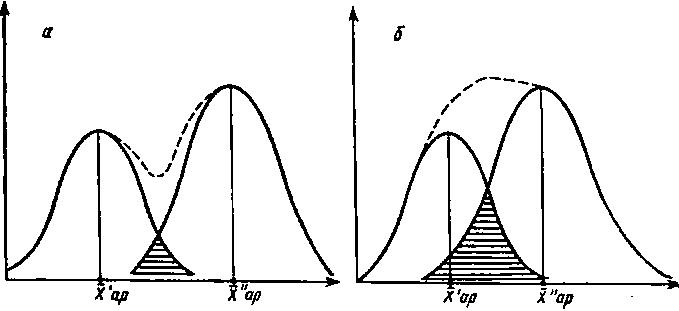
Рис. 1 Схематическая иллюстрация большей (б) или меньшей (а) степени близости двух эмпирических нормальных распределе­ний со средними значениями Х_ар1 и Х_ар2 .

Итак, критерий t Стьюдента направлен на оценку различий вели­чин средних X_ар1и X_ар2 двух выборок X₁ и X₂, которые распределены по нормальному закону. Одним из главных достоинств критерия является широта его применения. Он может быть использован для сопоставления средних у связных и несвязных выборок, при­чем выборки могут быть не равны по величине.

1. Случай несвязных выборок

В общем случае формула для расчета по t-критерию Стьюден­та такова:

|X_ар1- X_ар2|

tэ = √m₁² +m²₂ (1)

где т =  / n, есть так называемая ошибка средней, происходящая от представления Х_ар в качестве средней М некоторой генеральной совокупности;

 — стандартное отклонение;

n — количество числовых значений показателя (или количе­ство испытуемых);

Х_ар1 и Х_ар2—средние арифметические, различия между ко­торыми проверяются;

m₁² и m₂² — соответствующие квадраты ошибок средних величин.

Для практических расчетов можно использовать следующий вариант формулы:

________|X_ар1- X_ар2|__________ _• n₁ •n₂ • (n₁ +n₂ – 2)

tэ = √ (n₁ – 1) •  ₁² + (n₂ – 1) • ₂² √ n₁ + n₂ (2)

где

Х_ар1 и Х_ар2—средние арифметические, различия между ко­торыми проверяются;

n₁ и n₂ соответственно объемы первой и второй выборки,

₁² и ₂² — соответствующие стандартные отклонения.

Подсчет числа степеней свободы осуществля­ется по формуле:

k= n₁+ n₂ - 2 (3)

где n₁ и n₂ соответственно объемы первой и второй выборки.

Понятно, что при численном равенстве выборок k = 2 • n – 2.

В случае связанных выборок с равным числом измерений в каждой используется следующая формула t-критерия Стьюдента:

_ _( ∑ d_i _)______ _• n – 1

tэ = √ ∑ d_i² – (∑ d_i)²/ n √ n (4)

где di = х_i – у_i — разности между соответствующими значениями переменной X и переменной Y, a d среднее этих разностей,

n - объем выборки.

Число степеней свободы к определяется по формуле k = n - 1.

Для применения t-критерия Стьюдента необходимо соблюдать следующие условия:

1. Измерение может быть проведено в шкале интервалов и отно­шений.

2. Сравниваемые выборки должны быть распределены по нор­мальному закону.

F — критерий Фишера

Критерий Фишера позволяет сравнивать величины выбороч­ных дисперсий двух рядов наблюдений. Для вычисления F_эмп нуж­но найти отношение дисперсий двух выборок, причем так, что­бы большая по величине дисперсия находилась бы в числителе, а меньшая знаменателе.

Формула вычисления по критерию Фи­шера F такова:

D₁ ₁ ²

F = D₂ = ₂² (5)

Поскольку, согласно условию критерия, величина числителя должна быть больше или равна величине знаменателя, то значе­ние F_эмп всегда будет больше или равно единице, т.е. F_эмп ≥ 1. Чис­ло степеней свободы определяется также просто: df₁ = n₁- 1 для первой (т.е. для той выборки, величина дисперсии которой боль­ше) и df₂ = n₂ - 1 для второй выборки. В таблице Приложе­ния критические значения критерия Фишера находятся по величинам df₁ (верхняя строчка таблицы) и df₂ (левый столбец таблицы).

Для применения критерия F Фишера необходимо соблюдать следующие условия:

1. Измерение может быть проведено в шкале интервалов и отно­шений.

2. Сравниваемые выборки должны быть распределены по нор­мальному закону

Тема: «Назначение и использование методов непараметрической статистики»