3. Механические и тепловые свойства кристаллов

Вопросы

1. Дать определение упругой и пластической деформациям. Диаграмма напряжение-деформация.

2. Какова природа пластической деформации с точки зрения движения дислокаций? Чем отличается скольжение дислокаций от их переползания?

3. Как влияют точечные дефекты на механические свойства твердых тел? В чем секрет булатной стали?

4. Постоянные кристаллической решетки (см. Приложение) и массы атомов германия и кремния известны. Насколько различаются размеры первой зоны Бриллюэна Ge и Si и насколько различаются предельные частоты колебаний атомов в них (силу связи считать одинаковой)?

5. Почему у большинства полупроводников две моды поперечных оптических и две моды поперечных акустических колебаний обычно вырождены? Нарисуйте схематически колебательный спектр атомов трехмерной решетки в первой зоне Бриллюэна. Чем определяется минимальная и максимальная частоты колебаний?

6. Оценить фазовую и групповую скорости колебаний одноатомной решетки. Найти их максимальные и минимальные значения.

7. Физический смысл понятия "температура Дебая". Будет ли величина температуры Дебая зависеть от размеров кристалла? Почему теплоемкость всех веществ при высоких температурах описывается законом Дюлонга и Пти?

8. Определить относительную ошибку, которая будет допущена, если при вычислении теплоемкости вместо значения, вычисляемого по теории Эйнштейна (при T = Q_E), воспользоваться значением, определяемым законом Дюлонга и Пти.

9. Как тепловое расширение твердых тел (ангармонизм колебаний) зависит от характера энергии взаимодействия атомов в кристалле?

10. Показать, что если смещение частиц в кристаллической решетке твердого тела подчиняется закону Гука: F(x) = –x, то тепловое расширение отсутствует.

Задачи

3.1. Зная модуль упругости E и плотность , рассчитать скорость звука:

а) в кремнии ( = 2330 кг/м³, E = 10,110¹⁰ Н/м²);

б) в германии ( = 5360 кг/м³, E = 7,910¹⁰ Н/м²);

в) в двуокиси кремния ( = 2650 кг/м³, E = 5,710¹⁰ Н/м²).

3.2. Определить минимальные и максимальные частоты оптических и акустических колебаний в арсениде галлия, считая, что скорость звука составляет 510³ м/с.

Методические указания

Рассматривая колебания атомов в арсениде галлия как колебания одномерной решетки с базисом [4], можно оценить частоты оптических ^оп и акустических ^ак колебаний:

– минимальная частота ^ак (соответствует значению волнового вектора k = 0) равна нулю;

– максимальная частота ^ак (соответствует k = /2а – границе зоны Бриллюэна, где 2а – период решетки) , где  – коэффициент квазиупругой силы; М – масса более тяжелого атома;

– минимальная частота ^оп (соответствует k = /2а) , где m – масса более легкого атома;

– максимальная частота ^оп (соответствует k = 0) .

Масса Ga т =69,72 а.е.м.; масса As М = 74,92 а.е.м.; 1 а.е.м. (атомная единица массы) = 1,6610^–27 кг.

Коэффициент  можно оценить из формулы для скорости звука:

, (3.1)

совпадающей со скоростью в акустической ветви колебаний при k, близких к нулю.

3.3. Решить предыдущую задачу для фосфида индия.

3.4. Используя значения скорости звука, полученные при решении задачи 3.1, определить максимальную энергию оптических фононов (в электронвольтах): а) в кремнии; б) в германии.

3.5. Используя значения скорости звука, полученные при решении задачи 3.1, оценить минимальную энергию оптических фононов (в электронвольтах): а) в кремнии; б) в германии.

3.6. Используя значения скорости звука, полученные при решении задачи 3.1, оценить максимальную энергию акустических фононов (в электронвольтах): а) в германии, б) в кремнии.

3.7. Определить среднюю энергию линейного одномерного квантового осциллятора при температуре T = _E (_E = 200 К), где _E – характеристическая температура Эйнштейна.

Методические указания

Среднее значение энергии квантового осциллятора, приходящееся на одну степень свободы в теории Эйнштейна

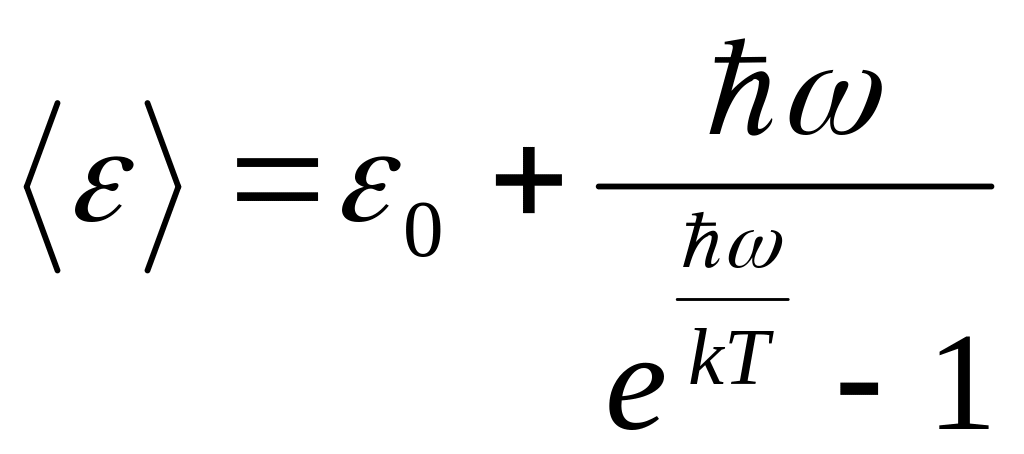, (3.2)

где – нулевая энергия; – постоянная Планка;  – циклическая частота колебаний; k – постоянная Больцмана; Т – абсолютная температура.

Характеристическая температура Эйнштейна

. (3.3)

3.8. Найти энергию фонона, соответствующего граничной частоте Дебая (_max), если характеристическая температура Дебая _D = 250 К.

3.9. Вычислить среднюю длину свободного пробега фононов в кварце (двуокиси кремния) при некоторой температуре, если при той же температуре: коэффициент теплопроводности  = 13 Вт/(мК), киломольная теплоемкость c = 44 кДж/(кмольК) и усредненное значение скорости звука  = 510³ м/с. Плотность кварца  = 2,6510³ кг/м³.

Методические указания

Коэффициент теплопроводности

, (3.4)

где с^v – теплоемкость единицы объема;  – скорость звука;  – средняя длина свободного пробега.

Теплоемкость единицы объема с^v можно выразить через киломольную теплоемкость с_к-м следующим образом.

Пусть с – теплоемкость, тогда ее можно выразить через с^v и с_к-м:

, (3.5)

где V – объем; т – масса;  – молярная масса; m/ – число киломолей.

Отсюда

. (3.6)

3.10. Вычислить максимальную силу, возвращающую атом твердого тела в положение равновесия, если коэффициент гармоничности  = 50 Н/м, а коэффициент ангармоничности  = 500 ГН/м².

Методические указания

Сила f(х), возвращающая частицу в равновесное положение при ангармонических колебаниях, определяется через коэффициенты  и :

. (3.7)

Условие экстремума дает возможность определить значение х, соответствующее максимальной силе, а затем и максимальную силу.

3.11. Определить, на сколько процентов изменится межатомное расстояние в твердом теле (при нагревании его до T = 400 К) по сравнению с равновесным расстоянием r₀ = 3 А, отвечающим минимуму потенциальной энергии. При расчетах принять коэффициент ангармоничности  = /(2r₀), где  – коэффициент гармоничности. Значение модуля Юнга Е = 10 ГН/м².

Методические указания

Линейный коэффициент теплового расширения

, (3.8)

где l – длина; dl/l – относительное изменение длины при изменении температуры на dT.

Коэффициент  может быть выражен через коэффициенты гармоничности  и ангармоничности :

, (3.9)

где k – постоянная Больцмана;  = r₀Е, где Е – модуль Юнга;   (1/2)(/r₀), тогда

. (3.10)

Из (3.8) следует:

, (3.11)

где Т = 400 К (нагревание от 0 до 400 К).

3.12. Определить микротвердость арсенида галлия, если при ее измерении под нагрузкой 100 г диагональ отпечатка составила 16 мкм.

Методические указания

Микротвердость определяется по формуле

, (3.12)

где  – угол между гранями пирамидки,  = 136, Р – нагрузка в кг/мм²; D – диагональ отпечатка в мм.

Расчет по формуле (3.12) дает

кг/мм²,

где Р₁ ‑ нагрузка в граммах; D₁ – диагональ отпечатка в микрометрах.