1. Энергия связи, структура и симметрия кристаллов. Методы определения структуры кристаллов

Вопросы

1. Перечислить основные типы межатомных связей. Показать, какие типы связей являются дальнодействующими, а какие – близкодействующими. Как это влияет на строение кристаллов?

2. Как влияет тип межатомных связей на физические свойства кристалла (электрические, оптические и др.)? Почему ковалентные кристаллы неплотно упакованы, а ионные имеют бóльшую плотность упаковки?

3. Какова природа упругости, пластичности и твердости кристаллов с точки зрения их межатомных связей?

4. Чем определяется длина волны рентгеновского, электронного и нейтронного излучения? Как различаются по разрешающей способности эти виды излучений?

5. Дать определение обратной решетки. Физический смысл узлов и плоскостей в обратной решетке.

6. Доказать, что пространственной решеткой, обратной ГЦК, будет ОЦК, и наоборот.

7. Перечислить основные экспериментальные дифракционные методы определения структуры кристаллов и охарактеризовать особенности каждого из них.

Задачи

1.1. Известно, что в кристалле, в котором связи обусловлены силами Ван-дер-Ваальса, равновесное межатомное расстояние r₀ = 0,15 нм, а энергия на 10 % меньше, чем в случае, когда учитываются только силы притяжения. Чему равна характерная длина , входящая в выражение для энергии

? (1.1)

1.2. В молекуле фтористого калия равновесное межядерное расстояние r₀ равно 0,267 нм, а энергия связи Е относительно энергии бесконечно удаленных ионов на 0,50 эВ на молекулу меньше энергии кулоновского притяжения, что обусловлено отталкиванием при перекрытии электронных оболочек. Известно, что сродство к электрону у фтора равно 4,07 эВ на электрон, а первый потенциал ионизации калия составляет 4,34 В. Покажите, что энергия, необходимая для разделения молекулы на два нейтральных атома, равна 0,945E.

1.3. На примере кристалла хлористого натрия объяснить физический смысл постоянной Маделунга A_l, входящей в выражение для энергии решетки E:

, (1.2)

где e – заряд электрона, а в качестве l может быть выбрано либо наименьшее расстояние r₀ между катионом и анионом, тогда A_r = 1,7476, либо длина ребра куба a, тогда A_a = 3,4951. Объяснить отличие A_r от A_a.

Методические указания

Нарисовать элементарную ячейку кристаллической решетки хлористого натрия. Записать энергию взаимодействия центрального иона с ионами первой, второй, третьей и т.д. координационных сфер, для чего определить радиусы этих сфер, выразив их значения через период решетки а (и через кратчайшее межатомное расстояние r₀), и определить соответствующие координационные числа. Записать знакопеременный ряд из слагаемых, числителем которых является координационное число, а знаменателем – относительные значения радиусов координационных сфер. Этот знакопеременный ряд сходится, и сумма его равна постоянной Маделунга.

1.4. Решить предыдущую задачу на примере кристалла хлористого цезия, для которого A_r = 1,7627; A_a = 2,035.

1.5. Определить, сколько атомов приходится на одну элементарную ячейку в кристаллах с простой, ОЦК, ГЦК и алмазной решеткой.

1.6. В кубической кристаллической решетке построить плоскости с индексами Миллера (121) и ( ).

1.7. Определить расстояние между ближайшими параллельными плоскостями {111} в кубической кристаллической решетке с периодом элементарной ячейки а.

1.8. Определить индексы плоскости, отсекающей на осях кубической решетки отрезки: A = 1a; B = 3a; C = 5a, где а – период решетки.

1.9. Определить наименьшие отрезки, отсекаемые на осях кубической решетки плоскостью ( ), и изобразить эту плоскость графически.

1.10. Вычислить, сколько атомов располагается на 1 мм² плоскостей (100) и (111) в кристаллической решетке кремния, если межатомное расстояние l = 0,2352 нм.

Решение

Кремний кристаллизуется в решетке алмаза, где межатомное расстояние l равно 1/4 большой диагонали куба. Поэтому период решетки а = = 40,2352 = = 5,4310^–10 м. Из рис. 1.1 следует, что на плоскости (100) элементарной ячейки находится два атома кремния (поскольку каждый угловой атом одновременно принадлежит четырем соседним ячейкам): п = 41/4 + 1 = 2. Отсюда поверхностная плотность атомов

N_S = n/S = n/a² = 2/(5,4310^–10)² = 6,7810¹⁸ м^–2 = 6,7810¹² мм^–2.

На рис. 1.2 показано расположение атомов на плоскости

(111). Равностороннему треугольнику площадью принадлежит в среднем два атома: п = 3   1/6 + 31/2 = 2. Поверхностная плотность атомов в этой плоскости

= 7,8410¹⁸ м^–2 = 7,8410¹² мм^–2.

1.11. Из узла алмазной решетки: а) записать оси на все атомы элементарной ячейки; б) записать соответствующие этим осям плоскости; в) нарисовать плоскости (222), (200) и (221).

1.12. Какие плоскости имеют максимальную плотность упаковки атомов в кристаллах: а) хлористого натрия; б) алмаза?

1.13. У каких плоскостей в структуре ГЦК максимальная плотность упаковки атомов? В каких направлениях в этих плоскостях линейная плотность расположения атомов максимальна?

1.14. Решить предыдущую задачу для структуры ОЦК.

1.15. Рассчитать плотность упаковки для решеток: а) алмаза; б) кубической примитивной; в) кубической объемноцентрированной; г) кубической гранецентрированной.

Методические указания

Плотность упаковки F – относительная доля объема кристаллической решетки, заполненного атомами. В расчете на элементарную ячейку с ребром а

, (1.3)

где Z – количество атомов, приходящихся на элементарную ячейку; V_ат – объем одного атома, ; V_яч – объем элементарной ячейки, V_яч =а³;

, (1.4)

где r – атомный радиус;

, (1.5)

где N_i – число атомов внутри ячейки; N_f – число атомов на ее гранях; N_е – число атомов на ребрах; N_c – число атомов в вершинах ячейки.

Тогда для решетки алмаза Z = 8, a = 8r, F = 0,34;

для кубической примитивной Z = 1, a = 2r, F = 0,524;

для ОЦК Z = 2, a = 4r, F = 0,68;

для ГЦК Z = 4, a = 4r, F = 0,74.

1.16. Показать, что в кристаллах могут быть оси вращения только 2-го, 3-го, 4-го и 6-го порядков.

Решение

Рассмотрим модель двумерного «кристалла», имеющего в горизонтальном направлении постоянную решетки а. Тогда в ряду А расстояние между 1-м и т-м атомами равно (т – 1)а. Теперь допустим, что симметрией данной решетки разрешен поворот на угол . При вращении вокруг атома 2 в направлении против часовой стрелки атом 1 переместится в положение, занятое прежде атомом 1. Аналогично при вращении по часовой стрелке вокруг (т – 1)-го атома атом т переместится в положение, занятое ранее атомом т. Очевидно, что атомы 1 и т принадлежат к ряду В, так что расстояние Х между ними должно быть кратно а, если поворот на угол  разрешен симметрией решетки. Предположим, что Х = ра, где р – неизвестное целое число. Разность двух неизвестных целых чисел т и р можно выразить через . Из рис. 1.3 с помощью очень простой тригонометрии получаем

Х = ра = (т – 3)а + 2а соs, (1.6)

откуда

соs = (3 + р – т)/2. (1.7)

При условии, что т и р целые числа, уравнение (1.7) имеет всего пять решений, которые представлены в табл. 1.1.

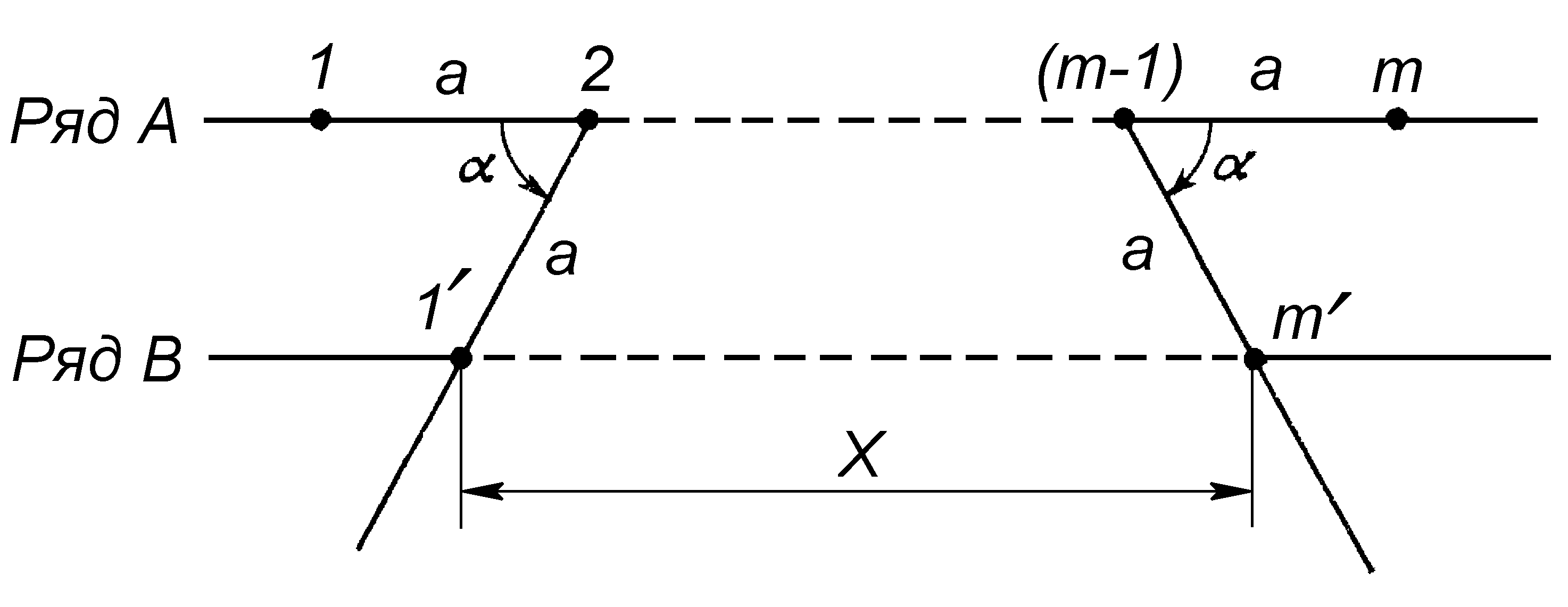
Рис. 1.3. Двумерная модель, показывающая,

какие углы вращения совместимы также

с трансляционной симметрией кристалла

Таблица 1.1

Решения уравнения (1.7) для вращений, разрешенных

в периодической решетке

р – т	соs		Порядок оси вращения
–1	1	0	1-й
–2	1/2	/3	6-й
–3	0	/2	4-й
–4	–1/2	2/3	3-й
–5	–1		2-й

1.17. Построить примитивные ячейки для непримитивных ячеек стандартных решеток Браве.

1.18. Вычислить период кристаллической решетки меди, если ее плотность равна 8920 кг/м³, а элементарная ячейка представляет собой гранецентрированный куб. Определить объем, приходящийся на один атом.

Решение

Рентгеновская плотность кристалла связана с периодом кубической решетки соотношением d = Кт/а³, где т – масса атома; К – число атомов, приходящихся на одну элементарную ячейку (кратность ячейки). В случае гранецентрированного куба К = 4. Учитывая, что т = А/N_А, где А – атомная масса; N_А – число Авогадро, получаем

.

На один атом решетки приходится объем

.

1.19. На дебаеграмме первая линия (от 0), полученная отражением от системы плоскостей (111) в кристалле меди, соответствует углу дифракции 2 = 43, где  – угол Брегга. Чему равен период решетки меди, если длина волны рентгеновских лучей 0,154 нм? Чему равен атомный радиус меди?

1.20. На дебаеграмме некоторого кубического кристалла, снятой на излучении меди К_ ( = 0,1542 нм), видны линии под углами Брегга : 12,3; 14,1; 20,2; 24,0; 25,1; 29,3; 32,2 и 33,1. Проиндицировать эти линии. Определить, является ли эти решетка примитивной, ГЦК, ОЦК и вычислить длину ребра ячейки.

Методические указания

Отличие в дебаеграммах простой кубической, ОЦК и ГЦК решеток связано с отсутствием некоторых рефлексов при отражении от сложных решеток (ОЦК, ГЦК) (учет структурного фактора [4]).

По формуле Вульфа-Брегга отражения от системы плоскостей (hkl) происходят под определенными углами

, (1.8)

где d_hkl – межплоскостное расстояние;  – угол отражения (угол Брегга);  – длина волны характеристического рентгеновского излучения; n – порядок спектра (п = 1, 2, 3, …).

, (1.9)

где а – период решетки.

При расчете возможных рефлексов по уравнению (1.8) принимают порядок спектра п = 1, а значения индексов Миллера h, k, l – 0, 1, 2, 3 и т.д. Для п = 2, 3 и более выводы не изменятся, так как

;

(1.10)

,

(например, d₁₁₁/2 = d₂₂₂, d₁₁₁/3 = d₃₃₃), т.е. при отражении в спектрах п= 2, 3, … порядков возникает рефлекс, соответствующий отражению от плоскостей (nh nk nl).

На дебаеграмме простой кубической решетки присутствуют отражения от всех плоскостей (hkl). Для ОЦК решетки все отражения hkl с нечетной суммой индексов гаснут; для ГЦК решетки гаснут все отражения hkl с индексами разной четности (нуль считается четным).

При постоянных значениях а и  из формул (1.8) и (1.9) видно

; (1.11)

.

Для простой кубической решетки первый угол  будет соответствовать рефлексу (100) – (h² + k² +l²) = 1, второй – (110) – (h² + k² +l²) =2, третий – (111) – (h² + k² +l²) =3 и т.д. (Индексы hkl -рефлексов – это произведение hkl на порядок спектра, поэтому рефлекс 100 для ОЦК решетки для порядка 2 будет равен 200 и разрешен.)

Для ОЦК решетки будут рефлексы с четной суммой (h + k +l), первый угол  будет соответствовать рефлексу (110) – (h² + k² +l²) = 2, второй угол – (200) – (h² + k² +l²) = 4, третий – (211) – (h² + k² +l²) = 6 и т.д.

Для ГЦК решетки будут индексы одной четности; первый угол соответствует рефлексу (111) – (h² + k² +l²) =3, второй угол – (200) – (h² + k² +l²) =4, третий угол – (220) – (h² + k² +l²) = 8 и т.д.

Поэтому для решения задачи следует посчитать sin² и проверить их отношения для нескольких углов: sin² ~ 3, 4, 8, 11, 12, 16, 19, 20. Это соответствует рефлексам (111), (200), (220), (311), (222), (400), (331), (420).

1.21. Определить угол, под которым пучок рентгеновских лучей с длиной волны 0,11 нм отражается в максимальном порядке дифракции от системы кристаллических плоскостей, расстояние между которыми 0,25 нм.

1.22. Вычислить углы дифракции ( = 2, где  – угол Брегга), соответствующие первым пяти линиям снятым на К_- линии меди ( = 0,1542 нм) дебаеграмм:

а) алюминия с постоянной решетки а = 0,404 нм (ГЦК решетка);

б) ванадия с а = 0,303 нм (ОЦК решетка).