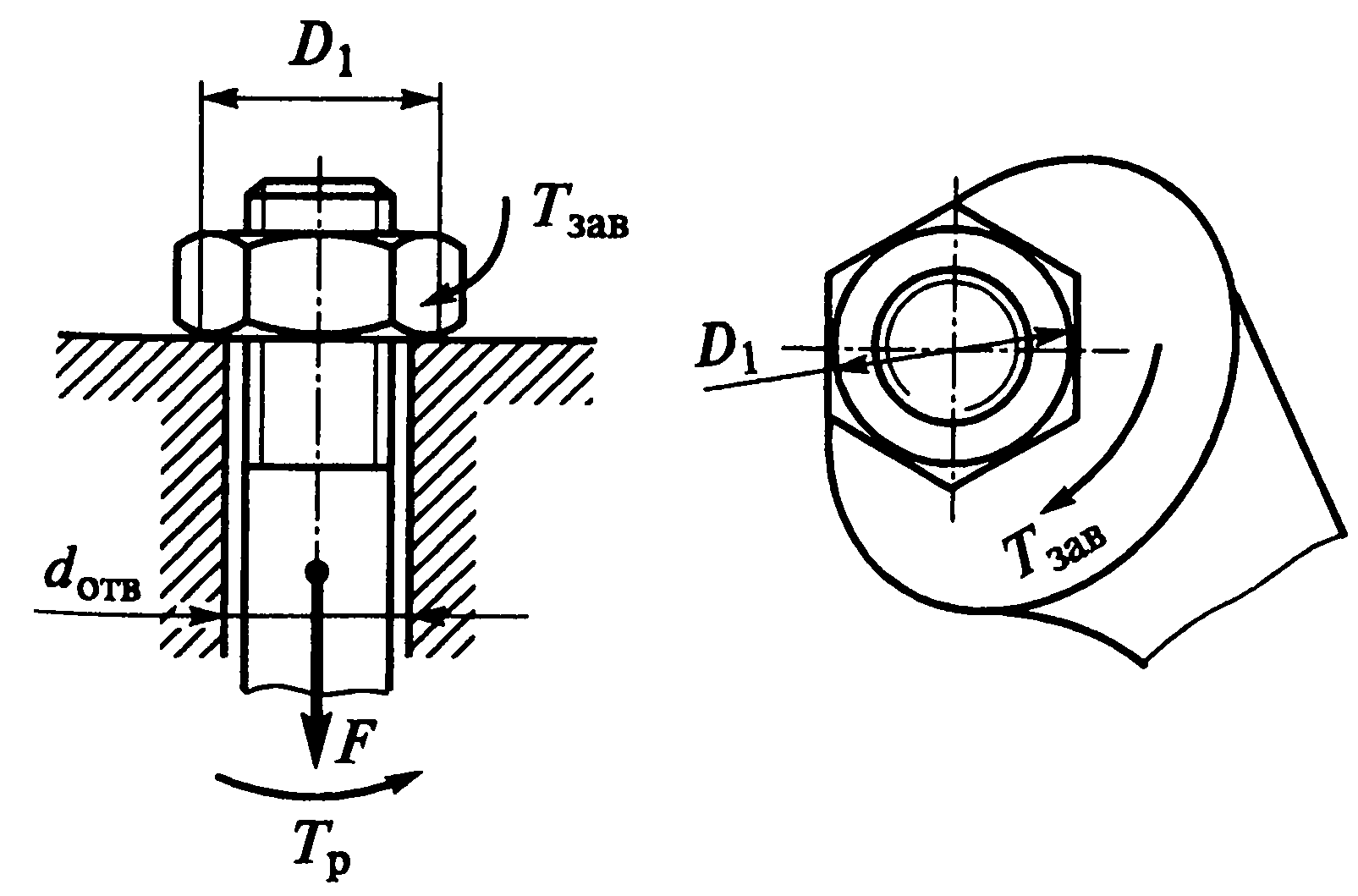
43. Теория винтовой пары. Зависимость между моментом, приложенным к гайке, и осевой силы на винте.

Е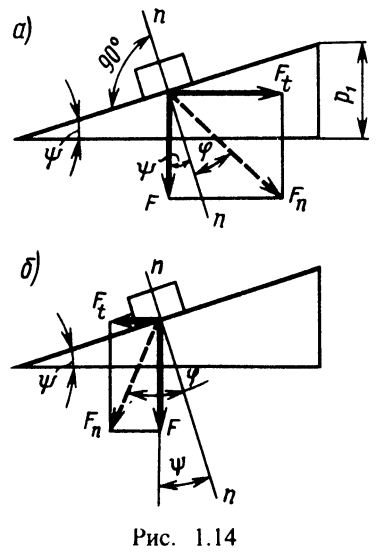 сли винт нагружен осевой силой F (рис. 1.13), то для завинчивания гайки к ключу необходимо приложить момент T_зав, а к стержню винта - реактивный момент T_р, который удерживает стержень от вращения. При этом можно записать: Т_зав = Т_т + Т_р, где Т_т — момент сил трения на опорном торце гайки; Т_р — момент сил трения в резьбе. T_T = Ff(D_ср/2), где D_cp = (D_l + d_ОTB) / 2; D_l - наружный диаметр опорного торца гайки; d_отв - диаметр отверстия под винт; f - коэффициент трения на торце гайки. F_t = 2T_p/d₂; F_t = F·tg(ψ + φ); => T_p = 0,5·F·d₂·tg(ψ + φ), где φ = arctg(f_пр) – угол трения в резьбе. Для крепежной метрической f_пр = 1,15f; для ходовой трапецеидальной симметричной f_пр = 1,03f; для ходовой упорной f_пр ≈ f; Т.о. Т_зав = 0,5·F·d₂·[( D_ср/d₂)f + tg(ψ + φ)]. При отвинчивании гайки окружная сила F_t и силы трения меняют направление (рис. 1.14,6): Т_отв = 0,5·F·d₂· [( D_ср/d₂)f + tg(ψ - φ)]. f ≈ 0,15

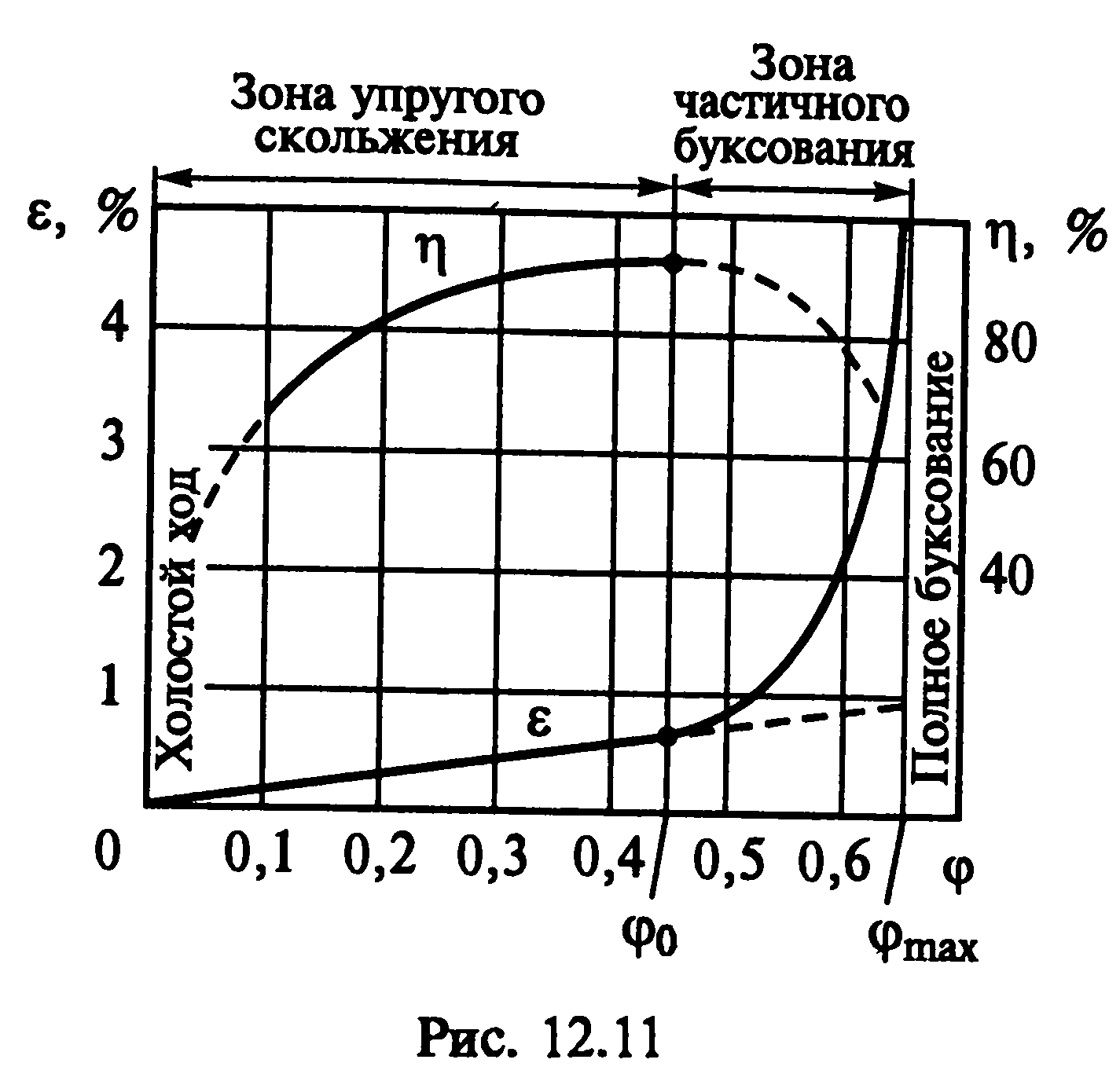
44. Скольжение в ременной передач. Кривые скольжения и кпд.

53. Расчет предварительно затянутого болта, когда внешняя нагрузка раскрывает стык деталей соединения.

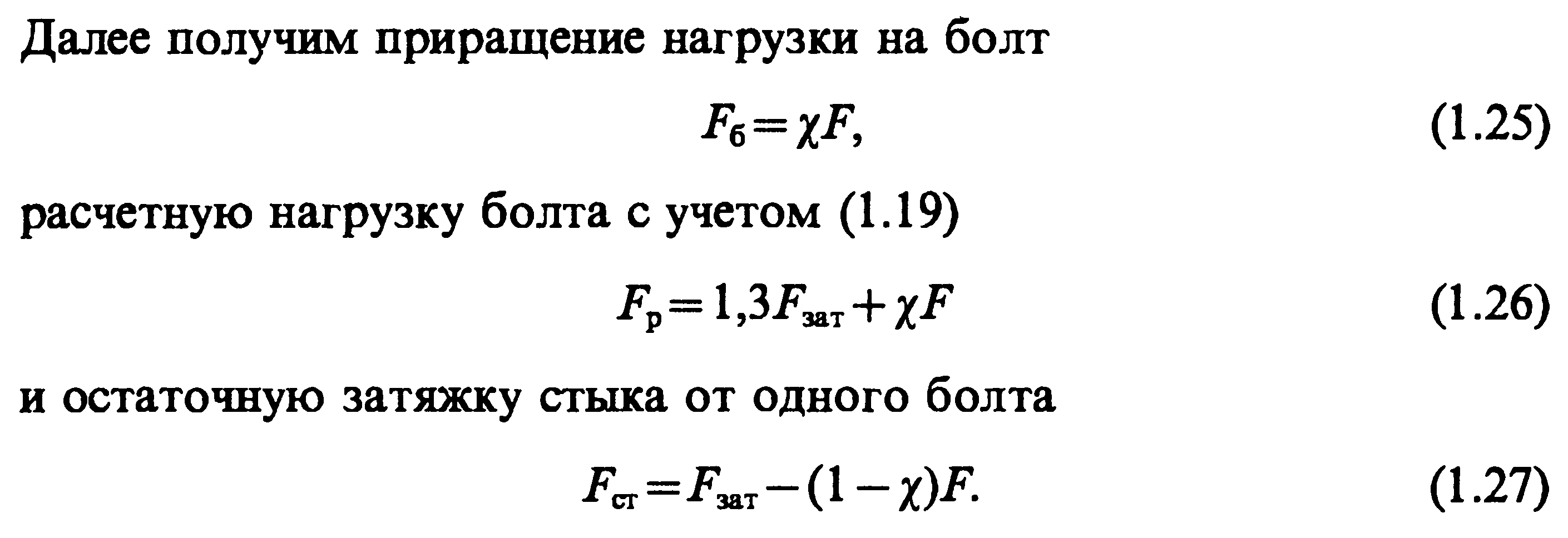
54. Критерии работоспособности и расчета приводных цепей. Допускаемое давление в шарнирной цепи.

Для большинства усло-

31. Расчет болтовое соединение, выполненного в 2 вариантах конструкции и нагруженного сдвигающей по стыку силой

Расчет на прочность затянутого и незатянутого болта: Растягивающая внешняя нагрузка без затяжки болтов: σ = F / [(π/4)d₁²] ≤ [σ], где [σ] = 0,6[σ_т] Растягивающая внешняя нагрузка с затяжкой болтов:

σ _ЭК = 1,3F_ЗАТ/[(π/4)d₁²] ≤ [σ], где [σ] = σ_Т / S_Т Статическая внешняя нагрузка: σ = 1,3F_Р / [(π/4)d₁²] ≤ [σ], где [σ] = σ_Т / S_Т при неконтролируемой затяжке и [σ] = σ_Т / (1,5…2,5) при контролируемой затяжке. Здесь F_P = F_ЗАТ + (0,2…0,3)F, F_ЗАТ = K_ЗАТF – при постоянной нагрузке K_ЗАТ = 1,25…2; при переменной нагрузке K_ЗАТ = 2,5…4; при мягкой прокладке K_ЗАТ = 1,3…2,5; при металлической фасонной прокладке K_ЗАТ = 2…3,5; при металлической плоской прокладке K_ЗАТ = 3…5; F – внешняя нагрузка соединения приходящаяся на один болт. Поперечная внешняя нагрузка, болты поставлены с зазором, затяжка неконтролируемая: σ_ЭК = 1,3F_ЗАТ/[(π/4)d₁²] ≤ [σ], где [σ] = σ_Т / S_Т Поперечная внешняя нагрузка, болты поставлены с зазором, затяжка контролируемая: σ_ЭК = 1,3F_ЗАТ/[(π/4)d₁²] ≤ [σ], где [σ] = σ_Т / (1,5…2,5) Поперечная внешняя нагрузка, болты поставлены без зазора: τ = F/[(π/4)d²i] ≤ [τ], где i – число плоскостей среза (на рисунке i = 2), τ = 0,4σ_Т при статической внешней нагрузке, τ = (0,2…0,3)σ_Т при переменной внешней нагрузке. σ_{с м} = F/(d·δ₂) ≤ [σ_{с м}], для крайней детали σ_{с м} = F/(2d·δ₂) ≤ [σ_{с м}], где для стали [σ_{с м}] = 0,8σ_т, для чугуна [σ_см] = (0,4…0,5)σ_в

35. Виды разрушения зубьев зубчатых колес. Основные критерии расчета зубьев на прочность. Поломка зубьев (рис. 8.11). Поломка связана с напряжениями изгиба. На практике чаще наблюдается выламывание углов зубьев вследствие концентрации нагрузки. Различают два вида поломки зубьев: поломка от больших перегрузок ударного или даже статического действия (предупреждают защитой привода от перегрузок или учетом перегрузок при расчете); усталостная поломка, происходящая от действия переменных напряжений в течение сравнительно длительного срока службы (предупреждают определением размеров из расчета на усталость). Особое значение имеют меры по устранению концентраторов напряжений (рисок от обработки, раковин и трещин в отливках, микротрещин от термообработки и т. п.).

Расчет на изгибную прочность прямозубой передачи. Напряжение в опасном сечении, расположенном вблизи хорды основной окружности: σ_F = F_t·l / W – F_r / A, где W = b_W·s² / 6 – момент сопротивления сечения при изгибе, A = b_W·s - площадь. Обозначим l’ = l / m, s’ = s / m, где m - модуль зубьев. После подстановки и введения расчетных коэффициентов: где K_F – коэффициент расчетной нагрузки, K_T – теоретический коэффициент концентрации напряжений. Далее обозначают: - безразмерный коэффициент, значения которого зависят только от формы зуба (размеры l’, s’, α_W) и в том числе от формы его галтели (коэффициент K_T). При этом для прямозубых передач расчетную формулу записывают в виде: σ_F = Y_FS·F_t·K_F / (b_W·m) ≤ [σF], где [σF] - допускаемое напряжение изгиба. Для проектных расчетов формулу решают относительно модуля путем замены b_W = ψ_m·m, F_t = 2T₁ / d₁, d₁ = z₁·m, тогда σ_F = 2T₁· K_F· Y_FS / (z₁· ψ_m·m³)

Расчет на контактную прочность. Формула Герца. На рис. 8.7 изображен пример сжатия двух цилиндров с параллельными осями. σH = 0,418√(qE_ПР/ρ_ПР), где Е_ПР = 2Е₁Е₂/(Е₁ + Е₂) и 1/ρ_ПР = 1/r₁ ± 1/r₂. При контакте цилиндра с плоскостью r₂ = ∞. Знак минус в формуле для 1/ρ_ПР относится к случаю внутреннего контакта (когда поверхность одного из цилиндров вогнутая).