
- •21. Определение допускаемых напряжений при расчетах зубчатых передач на выносливость
- •22.Конструкции разъемного соединения призматической шпонкой и ее разновидностями
- •51. Силы в цепной передаче. Динамика цепной передачи.
- •17. Самоторможение и кпд винтовой пары.
- •52. Распределение осевой нагрузки по виткам резьбы.
- •39. Основы теории гидродинамической смазки для расчета опор жидкостного трения.
- •40. Расчет соединений, включающих группу болтов
- •47. Цепные передачи. Область применения. Геом и кинем характеристики.
- •48. Распределение нагрузки между телами качения в подш качения. Конт-е напряжения.
- •45. Рачет на прочность сварных швов таврового соединения
- •30. Практический подбор подшипников по динамической грузоподъемности.
- •49. Конструкции приводных цепей: роликовых, втулочных, зубчатых.
- •50. Критерии расчета и работоспособности подшипников качения
- •13. Конические зубчатые передачи. Особ. Геометрии, кинемат., изг-я, сборки.
- •14. Анализ конструкций болтового соединения. Без зазора, с зазором.
- •3. Резьба. Основные понятия и определения. Геометрические параметры метрической резьбы. Изготовление.
- •4. Конструкции основных типов подшипников
- •19. Особенности расчета зубъев конических прямозубых колес по напряжениям изгиба.
- •28. Особенности расчета нагрузки радиально-упорных подшипников качения при проверке их ресурса
- •37. Проверочный расчет вала передачи на прочность.
- •32. Предохранительные муфты приводов. Назначение, основные конструктивные схемы и принцип действия.
- •32. Компенсирующие муфты приводов. Назначение устройство и принцип действия.
- •33. Коэффициент расчетной нагрузки в зубчатых передачах
- •3 4. Расчет на прочность угловых сварных швов нахлесточного соединения, нагруженного моментом.
- •43. Теория винтовой пары. Зависимость между моментом, приложенным к гайке, и осевой силы на винте.
- •36. Расчет на прочность стержня болта при нагружении силой предварительной затяжки.
- •55. Основные типы фрикционных передач и вариаторов. Кинематические и силовые зависимости в передаче. Диапазон регулирования вариаторов.
- •2 Конструкция и область применение радиально- упорных подшипников качения.
- •29. Механические передачи. Классификация, основные характеристики. Важнейшие силовые зависимости в передаче.
- •11. Расчет зубьев прямозубых цилиндрических колес по напряжениям изгиба
- •12. Конструкция и область применения самоустанавливающихся подшипников качения.
- •9. Критерии работоспособности и расчета типовых эл-ов машин.
- •5. Анализ конструкций соединений основными крепежными деталями(болтом, винтом и шпилькой).
- •6. Опоры скольжения. Режимы трения и критерии расчета подшипников скольжения
- •57. Кинематика червячных передач. Коэффициент полезного действия передачи. Усилия в червячном зацеплении.
- •8. Подшипники качения
- •18. Ременные передачи
- •18. Порядок проектного расчёта клиноременной передачи
- •20. Сварные соединения
- •Известны следующие виды стопорения.
- •23. Шпоночные соединения
- •24 Ременные передачи
- •25. Шлицевые соединения
- •27. Конические зубчатые передачи
- •27. Расчёт зубьев на изгиб
- •38. Критерии расчёта эвольвентных зубьев
- •38. Расчёт зубьев на контактную выносливость
- •46. Расчёт номинальной долговечности подшипника
- •58. Муфты
21. Определение допускаемых напряжений при расчетах зубчатых передач на выносливость



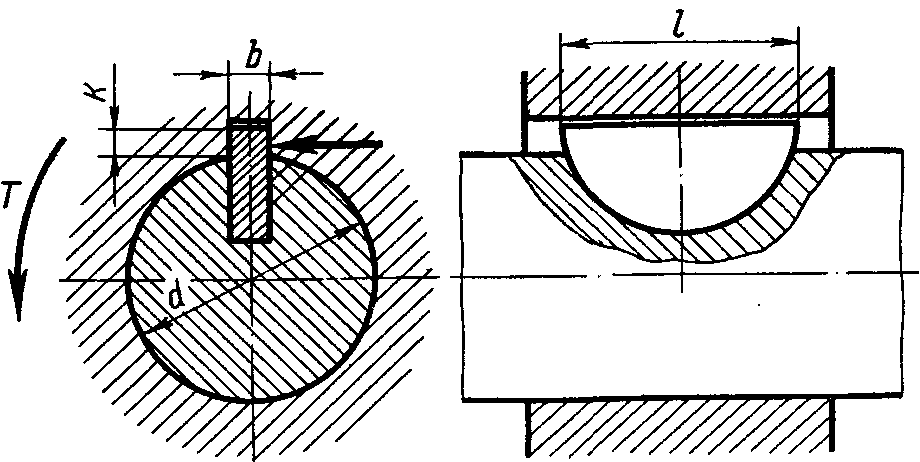
22.Конструкции разъемного соединения призматической шпонкой и ее разновидностями
Шпоночные соединения осуществляются при помощи шпонок, которые устанавливаются в пазах вала и ступице колеса.
Достоинства: простота разборки/сборки, надёжность в эксплуатации.
Недостатки: ослабление вала шпоночными пазами, высокая концентрация напряжений.
Шпоночные соединения делятся на две группы:
1) Ненапряжённые, те которые не вызывают деформации вала (призматические и сегментные)
2) Напряжённые (клиновые, тангенциальные)
1
 – вал
– вал
2 – ступица колеса
3 – призматическая шпонка
4 – распорная втулка
b – ширина шпонки
h – высота шпонки
t1 – глубина шпоночного паза
t2 – глубина шпоночного паза на ступице.
Д лина
шпонки выбирается из стандартного ряда.
Шпонка подбирается по диаметру вала.
Рабочая длина – длина шпонки по
горизонтальному участку.
лина
шпонки выбирается из стандартного ряда.
Шпонка подбирается по диаметру вала.
Рабочая длина – длина шпонки по
горизонтальному участку.
Обычно рассчитывают по напряжениям смятия.
В продольном сечении возникают напряжения среза.
С
 егментная
шпонка глубже посажена в вал. Предохраняет
от выворачивания, но при этом глубина
паза на валу больше, это ослабляет вал.
егментная
шпонка глубже посажена в вал. Предохраняет
от выворачивания, но при этом глубина
паза на валу больше, это ослабляет вал.
 Используют
для передачи небольших моментов или
просто для укрепления деталей на валу.
Используют
для передачи небольших моментов или
просто для укрепления деталей на валу.
Проверка и по смятию и по срезу.


51. Силы в цепной передаче. Динамика цепной передачи.




17. Самоторможение и кпд винтовой пары.
52. Распределение осевой нагрузки по виткам резьбы.


О бозначим
ΔА, ΔB,
ΔC, ΔD
перемещения соответствующих точек.
Вследствие растяжения участка АВ винта
ΔB < ΔА,
а вследствие сжатия участка CD гайки ΔD
< ΔC .
Относительное перемещение точек А и D,
В и С: ΔАD
= ΔА - ΔD;
ΔBC = ΔB
- ΔC; Учитывая
предыдущие неравенства, находим ΔАD
> ΔBC.
Следовательно, нагрузка первого витка
больше нагрузки второго и т. д. График
распределения нагрузки по виткам,
полученный на основе решения системы
уравнений для стандартной шестивитковой
гайки высотой Н=0,8d, изображен на рис.
1.15, б. График свидетельствует о значительной
перегрузке нижних витков и нецелесообразности
увеличения числа витков гайки, так как
последние витки мало нагружены. По этому
условию нецелесообразно применение
мелких резьб (при высоте гайки Н=const).
бозначим
ΔА, ΔB,
ΔC, ΔD
перемещения соответствующих точек.
Вследствие растяжения участка АВ винта
ΔB < ΔА,
а вследствие сжатия участка CD гайки ΔD
< ΔC .
Относительное перемещение точек А и D,
В и С: ΔАD
= ΔА - ΔD;
ΔBC = ΔB
- ΔC; Учитывая
предыдущие неравенства, находим ΔАD
> ΔBC.
Следовательно, нагрузка первого витка
больше нагрузки второго и т. д. График
распределения нагрузки по виткам,
полученный на основе решения системы
уравнений для стандартной шестивитковой
гайки высотой Н=0,8d, изображен на рис.
1.15, б. График свидетельствует о значительной
перегрузке нижних витков и нецелесообразности
увеличения числа витков гайки, так как
последние витки мало нагружены. По этому
условию нецелесообразно применение
мелких резьб (при высоте гайки Н=const).
39. Основы теории гидродинамической смазки для расчета опор жидкостного трения.
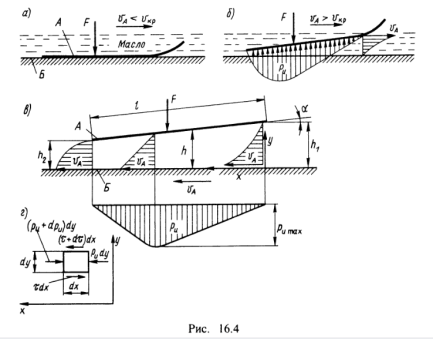
Исследование режима жидкостного трения в подшипниках основано на гидродинамической теории смазки. На рис. 16.4 показаны две пластины А и Б, залитые маслом и нагруженные силой F. Пластина А движется относительно пластины Б со скоростью vA. Если скорость vA мала (рис. 16.4, а), то пластина А выжимает масло с пластины Б. Поверхности пластин непосредственно соприкасаются. При этом образуется полужидкостное трение.
При достаточно большой скорости vA (рис. 16.4, б) пластина А поднимается в масляном слое и принимает наклонное положение. Между пластинами образуется сужающий зазор, заполненный маслом, а движение происходит в условиях жидкостного трения. Переход к режиму жидкостного трения происходит при некоторой скорости, называемой критической vск. Основополагающим является закон Ньютона:
 г
г![]() де
τ — напряжение сдвига от внутреннего
трения при сдвиге слоев жидкости, μ —
динамическая вязкость жидкости, Па •
с, v — скорость течения, м/с. Физический
смысл закона можно объяснить так.
Два тонких соседних слоя имеют некоторую
разность скоростей. На общей границе
слоев происходит сдвиг. Сопротивление
сдвигу пропорционально интенсивности
изменения скоростей в поперечном
направлении или производной dv/dy.
Коэффициент пропорциональности μ
зависит от свойств жидкости и определяется
экспериментально. Используя этот закон,
можно найти все другие характеристики
потока жидкости. Продифференцировав
уравнение Ньютона, получим:
де
τ — напряжение сдвига от внутреннего
трения при сдвиге слоев жидкости, μ —
динамическая вязкость жидкости, Па •
с, v — скорость течения, м/с. Физический
смысл закона можно объяснить так.
Два тонких соседних слоя имеют некоторую
разность скоростей. На общей границе
слоев происходит сдвиг. Сопротивление
сдвигу пропорционально интенсивности
изменения скоростей в поперечном
направлении или производной dv/dy.
Коэффициент пропорциональности μ
зависит от свойств жидкости и определяется
экспериментально. Используя этот закон,
можно найти все другие характеристики
потока жидкости. Продифференцировав
уравнение Ньютона, получим:
Основное уравнение гидродинамики для установившегося двухмерного течения жидкости:
Давление масла в зазоре, уравновешивающее внешнюю нагрузку F, а движение пластины А происходит при жидкостном трении.
И![]()
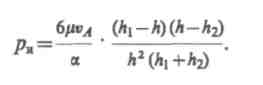 спользуя
полученные решения, можно сделать
следующие выводы: 1) Так как расход Q
жидкости одинаков во всех сечениях
сужающегося зазора, то средняя скорость
течения должна увеличиваться
справа
налево.2) Установим зависимость давления
от толщины масляного
слоя. В среднем
сечении h=(hi + h2)/2. Следовательно, давление
обратно пропорционально толщине
масляного слоя.
спользуя
полученные решения, можно сделать
следующие выводы: 1) Так как расход Q
жидкости одинаков во всех сечениях
сужающегося зазора, то средняя скорость
течения должна увеличиваться
справа
налево.2) Установим зависимость давления
от толщины масляного
слоя. В среднем
сечении h=(hi + h2)/2. Следовательно, давление
обратно пропорционально толщине
масляного слоя.
3) одним из условий образования режима жидкостного трения является наличие сужающегося зазора, который принято называть клиновым.
Таким образом, для образований режима жидкостного трения необходимо соблюдать следующие основные условия: 1) между скользящими поверхностями должен быть зазор клиновой формы; 2) масло соответствующей вязкости должно непрерывно заполнять зазор; 3) скорость относительного движения поверхностей должна быть достаточной для того, чтобы в масляном слое создалось давление, способное уравновесить внешнюю нагрузку.
