Лабораторная работа № 1 Тема: Экстраполяционные методы прогнозирования

1. Цель и содержание лабораторной работы

Целью лабораторной работы является освоение студентами теоретических знаний, получение при изучении методов социально-экономического прогнозирования, приобретение практических навыков расчёта прогнозных значений основных технико-экономических показателей различных видов деятельности предприятий топливно-энергетического комплекса.

Экстраполяция – самый распространённый и разработанный среди всей совокупности методов прогнозирования. Сущность его заключается в изучении динамических (временных) рядов, описывающих изменение некоторого показателя (параметр) во времени, выявление тенденции и продление ее в бедующее. Любое будущее состояние показателя прогноз рассматривает как результат предшествующих состояний. В настоящее время экстраполяционные методы широко используются в стратегическом управлении и планировании.

Принципиальная возможность прогнозирования основывается на предположении о закономерном характере изменения различных показателей и на инерционности технико-экономических процессов.

Уровни динамических рядов формируются под совокупным влиянием множества длительно и кратковременно действующих факторов, в том числе и случайных. Динамический ряд показателей может быть представлен в следующем виде:

yt = ŷt + Et ,

(1.1)

где ŷ_t - тренд (детерменирующая неслучайная компонента);

E_t - стохастическая случайная компонента (помеха), отражающая случайные колебания и имеющая нормативный закон распределения.

Специфическая черта прогнозной экстраполяции – предварительная обработка числового ряда, направленная на снижение влияния случайной составляющей (минимизация случайных отклонений точек ряда от некоторой плавной кривой, предполагаемого тренда), т.е. приближение её к тренду.

Задача прогноза состоит в определении вида экстраполирующих функций ŷ_t и E_t на основе исходных данных.

Промежуток времени, на который разрабатывается прогноз, называется периодом упреждения прогнозов, а максимально возможный период упреждения – горизонтом прогнозирования.

По форме упреждения различают точечные и интервальные прогнозы. В первом случае прогноз задаётся одним числом, во – втором указывается интервал, к которому с определённой вероятностью принадлежит прогнозируемая величина.

При прогнозировании ведётся наблюдение за процессом (рис. 1.1) и вычисляется его будущее значение в упреждённой точке, оценивается математическое ожидание процесса, величина интервала, в которой с заданной вероятностью попадает будущее значение прогноза.

у₅

у₄

у₂

у₃

у₁

Рис 1. 1 Точечный и интервальный прогнозы

В настоящей лабораторной работе используется алгоритм экстраполяции динамических рядов развития показателя прогнозируемого явления по ретроспективным данным путём статистического моделирования.

Постановка задачи

В лабораторной работе № 1 необходимо составить прогноз величины технико-экономического показателя y_t производственной деятельности предприятия отрасли, предсказав его возможную величину на основе статистических данных о его изменении за несколько предыдущих лет.

Исходные данные для расчета даются в табл. П. 1.1 и представляют собой информацию о величине прогнозируемого показателя на интервале времени за несколько предыдущих лет [t₁; t₂ …t_n].

Совокупность числовых значений показателя y_t образует динамический ряд y_t = {y₁, y₂…y_n} на отрезки времени T = {t₁, t₂…t_n}. Количество числовых значений, необходимых для решения поставленной задачи должно быть не менее 8.

2. Методические положения расчета перспективных технико-экономических показателей деятельности предприятия на основе экстраполяционного метода прогнозирования

Этап 1. Установление наличия и тесноты связи между величиной прогнозируемого показателя и фактором времени.

1. Определение точечной оценки коэффициента корреляции по формуле 1.2:

,

(1.2)

где y_ti – текущее значение показателя y_t (t = 1…n),

t_i - текущее значение показателя t (i = 1…n),

n – количество лет, за которые собраны статистические данные о значении показателя y_t.

По величине r_yt определяется сила взаимосвязи y_t и t при наличии между ними линейной связи. Чем ближе r_yt к «+1» или «–1», тем ближе связь между y_t и t к линейной. Наличие нелинейной связи определяется с помощью корреляционного отношения (расчет см. далее).

2. Проверка значения рассчитанного коэффициента корреляции по критерию

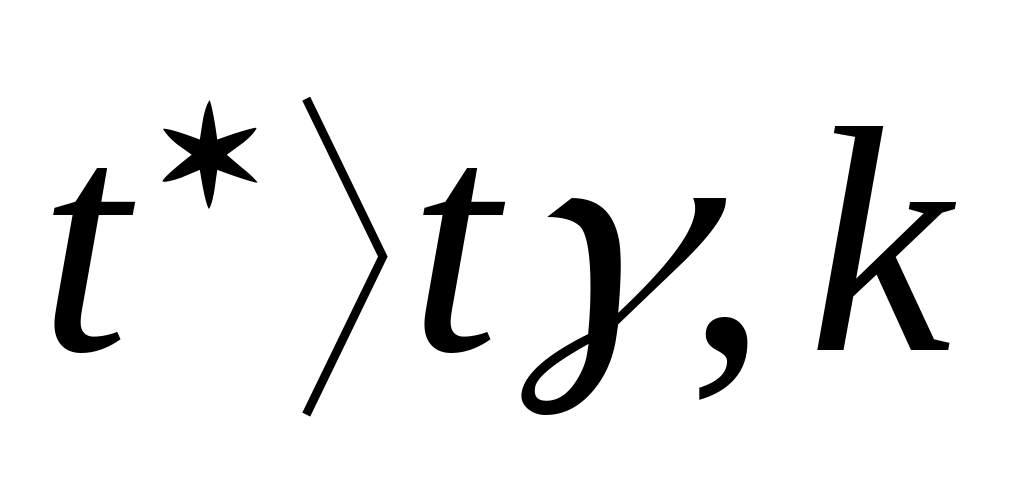
(1.3)

где - коэффициент оценки достоверности гипотезы о значимости коэффициента парной корреляции (табл. П.1.1);

k = n - 2 – число степеней свободы (характеристика суммы квадратов (отклонений), показывает, сколько отклонений в сумме квадратов может изменяться "свободно”)

- вход в таблицу ;

- уровень значимости гипотезы.

При выполнении критерия (1.3) гипотеза о значимости коэффициента парной корреляции подтверждается, т. е. величина y_t зависит от фактора времени.

Этап 2. Выбор вида математической модели, описывающей взаимозависимости y_t и t.

2.1 Построение графика изменения показателя y_t на интервале [t₁, t_n].

2.2 Выбор вида математической модели, описывающей взаимозависимость y_t и t

Наиболее простой путь выбора формы кривой, описывающей динамику показателя y_t., визуальный – выбор формы кривой на основе графически построенного ряда динамики (этап 2.1). В табл. 1. 1 приводятся перечень наиболее употребляемых видов кривых, на основе которых выбирают математическую модель и анализируют данные.

Таблица 1. 1