9. Метод резолюції в алгебрі висловлень, його застосування.

Метод резолюції є основним методом отримання виводів в програмах, що базуються на логіці предикатів.

Проте метод резолюцій застосовний до формул логіки предикатів не будь-якого вигляду, а тільки до таких, які подані у вигляді множини диз’юнктів. Тому для застосування методу резолюції спочатку необхідно виконати відповідні перетворення: формулу подати у вигляді КНФ, а тоді записати відповідну множину диз’юнктів.

Основна ідея методу резолюції полягає в:

1. П 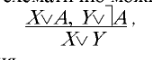еревірці того, що містить S порожній диз’юнкт,

2. Перевірці того, чи не виводиться порожній диз’юнкт з S, якщо порожнього диз’юнкта не містить.

На кожному кроці революційного процесу застосовується єдине правило виводу – правило резолюції, яке схематично можна подати у такому вигляді: (X, A, Y – висловлення).

Перед тим, як застосовувати правило резолюції, необхідно зробити певну підстановку і здійснити уніфікацію предикатів (зробити їх однаковими).

Приклад методу:

1. Якщо Наталка прочитала «12 стільців», то вона передала Павлові книжку;

2. якщо Наталка не передала книгу Павлові

Отже, вона не прочитала її.

А – прочитала, В- передала

А В, ˥В |= ˥A

1. А  В ≡˥А \/ В

2. ˥В

3. А

1. ˥А \/ В

2. ˥В

3. А

4. ˥А (1,2)

5. □ (4,3)

9. Застосування алгебри висловлень для аналізу і синтезу комбінаційних схем.

Під комбінаційною схемою розумітимемо технічний пристрій, який служить для перетворення дискретних повідомлень і має n входів і m виходів і такий, що сукупність вихідних сигналів в кожний дискретний момент часу однозначно визначається вхідними сигналами, які подаються на вхід в той самий момент часу. Сигнали, які подаються на входи і знімаються з виходів, можуть приймати тільки значення “1” і “0”. Такими сигналами можуть, наприклад, бути високий і низький рівні напруги. Отже, комбінаційна схема перетворює деяке n-буквене слово в двійковому алфавіті в m-буквене слово в тому самому алфавіті.

Комбінаційні схеми найчастіше будують з елементарних (базових) логічних елементів (схем), які реалізують найпростіші логічні операції.

Умовні графічні позначення базових логічних елементів показано на рис.1.

НЕ І АБО виключаюче І-НЕ АБО-НЕ

АБО

Рис. 1

Логічний елемент, який реалізує операцію заперечення, називається елементом “НЕ”, або інвертором. Він має один вхід, на який подається сигнал, що відповідає булевій змінній x (якщо є сигнал, =1, якщо немає сигналу, =0), і один вихід, на якому виникає сигнал . Логічний елемент, який реалізує операцію кон’юнкції, називається елементом “І”, або збігом. Логічний елемент, який реалізує операцію диз'юнкції, називається елементом “АБО” (відокремленням). Логічний елемент “виключаюче АБО” реалізує операцію заперечення еквіваленції (її ще називають сумою Жегалкіна, операцією XOR, додаванням за модулем 2). Елементи “І-НЕ” і “АБО-НЕ” відповідно реалізують операції штрих Шеффера і стрілку Пірса.

Часто доводиться розв'язувати задачі на аналіз та синтез схем.

Задача на аналіз комбінаційної схеми полягає в тому, щоб математично описати цю схему (побудувати її математичну модель), тобто знайти відповідну булеву функцію (відповідну логічну формулу). Таку задачу можна розв'язати, розкладаючи схему на підсхеми. Знайдену логічну формулу доцільно, по можливості, спростити, замінивши такою рівносильною формулою, яка містить меншу кількість елементів.

Задача на синтез конкретної схеми полягає в тому, щоб для заданої булевої функції побудувати відповідну їй найпростішу схему.

Проектуючи комбінаційну схему, рідко вдається відразу записати її структурну формулу. На першому етапі переважно використовується словесний опис задач, що розв'язуються за допомогою схем, на основі якого вдається скласти таблицю, яка пов’язує чисельні значення вхідних і вихідних логічних змінних. Перехід від таблиці до логічної формули є другим етапом синтезу комбінаційної схеми. Третім етапом є спрощення (якщо це можливо) або мінімізація логічної формули. І на останньому етапі будують комбінаційну схему за спрощеною формулою.

Отже, кожній контактній схемі відповідає певна булева функція (формула логіки висловлень) і, навпаки, кожній такій функції (формулі) відповідає деяка контактна схема.

Приклад Скласти логічну схему, яка має таку структурну формулу

 x y.

Л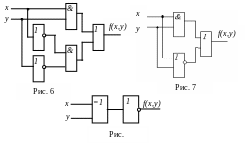 егко бачити, що відповідна логічна схема матиме два входи і складатиметься з п’яти логічних елементів (рис. 6).

Оскільки дана формула рівносильна такій

 ( x  y )

то можна побудувати схему, яка містить лише 4 логічних елементи (по одному “І” і “НЕ” та два елементи “АБО”). Якщо використати елемент “АБО-НЕ”, то можна обійтися лише трьома елементами (рис. 7), якщо використати логічний елемент “виключаюче АБО”, то достатньо буде й двох елементів (рис. 8).