5.Булеві функції. Питання функціональної повноти.

Булева функція (або логічна функція, або функція алгебри логіки) від n змінних - в дискретної математики відображення B n → B, де B = {0,1} - булево безліч. Елементи булева безлічі 1 і 0 зазвичай інтерпретують як логічні значення "істинно" і "помилково", хоча в загальному випадку вони розглядаються як формальні символи, що не несуть певного сенсу. Невід'ємне ціле число n називають арністю або місцевістю функції, в разі n = 0 булева функція перетворюється в булеву константу. Елементи декартова твори B n називають булевими векторами. Безліч всіх булевих функцій від будь-якого числа змінних часто позначається P 2, а від n змінних - P 2 (n). Булеві функції названі так за прізвищем математика Джорджа Буля. Кожна булева функція арності n повністю визначається завданням своїх значень на своїй області визначення, тобто на всіх булевих векторах довжини n. Число таких векторів дорівнює 2 n. Оскільки на кожному векторі булева функція може приймати значення або 0, або 1, то кількість всіх n-арних булевих функцій дорівнює 2 лютого n. Тому в цьому розділі розглядаються тільки найпростіші і найважливіші булеві функції. Те, що кожна булева функція задається кінцевим масивом даних, дозволяє представляти їх у вигляді таблиць. 1.1. Нульарние функції

При n = 0 кількість булевих функцій зводиться до двох 2 2 0 = 2 1 = 2, перша з них тотожно дорівнює 0, а друга 1. Їх називають булевими константами - тотожний нуль і тотожна одиниця.

1.2. Унарні функції

При n = 1 число булевих функцій дорівнює 2 2 1 = 2 2 = 4. Визначення цих функцій міститься в наступній таблиці.

Таблиця значень булевих функцій від однієї змінної: x 0 x̅ x 1

0 0 1 0 1

1 0 0 1 1

Назви булевих функцій від однієї змінної: Позначення Назва

0 тотожний нуль, тотожна брехня, тотожне "НІ"

x̅, x, x ' заперечення, логічне "НІ", "НЕ", "НІ", "NOT" (англ.), "NO" (англ.)

x тотожна функція, логічне "ТАК", "YES" (англ.)

1 тотожна одиниця, тотожна істина, тотожне "ТАК", тавтологія.

Функціональна повнота

Визначення. Множина функцій алгебри логіки А називається повною системою (в Р₂), якщо будь-яку функцію алгебри логіки можна виразити формулою над А.

Теорема 1[1, ст.6]. Система А={ } є повною.

Доведення. Якщо функція алгебри логіки відмінна від тотожного нуля, то f виражається у вигляді досконалої диз’юнктної нормальної форми, в яку входять лише диз’юнкція, кон’юнкція та заперечення. Якщо ж , то . Теорема доведена.

Лема 1[1, ст.6]. Якщо система А – повна, і будь-яка функція може бути виражена формулою над іншою системою В, то В – теж повна система.

Доведення. Розглянемо довільну функцію алгебри логіки і дві системи функцій А={g₁, g₂,…} і B={h₁, h₂,…}. Оскільки система А повна, функція може бути виражена у вигляді формули над нею , де , тобто функція представляється у вигляді , що означає що вона може бути представлена формулою над В. Перебираючи таким чином всі функції алгебри логіки, отримаємо, що система В також повна. Лема доведена.

Теорема 2[1, ст.6]. Такі системи є повними в Р₂

1. ;

2. ;

3. ;

4. 

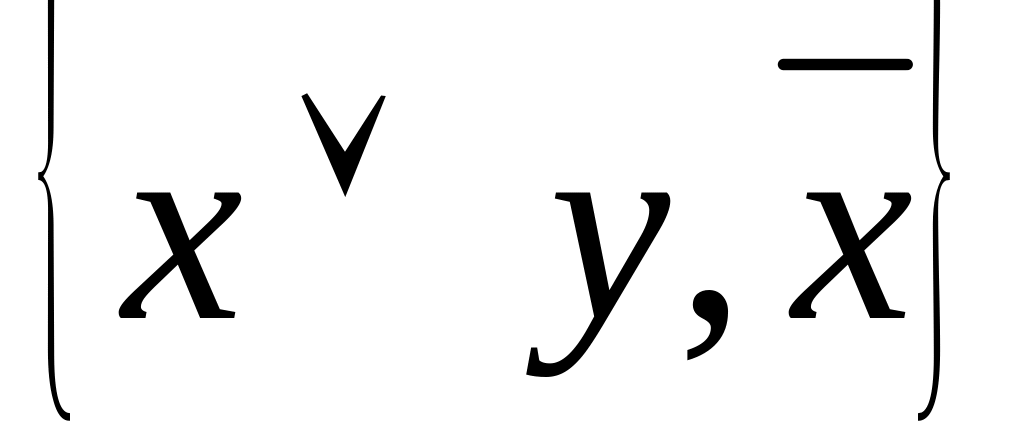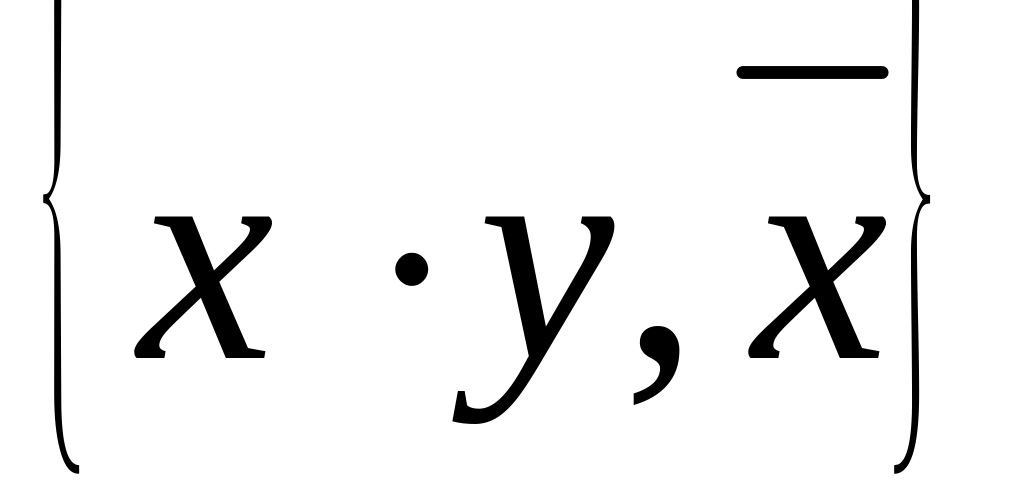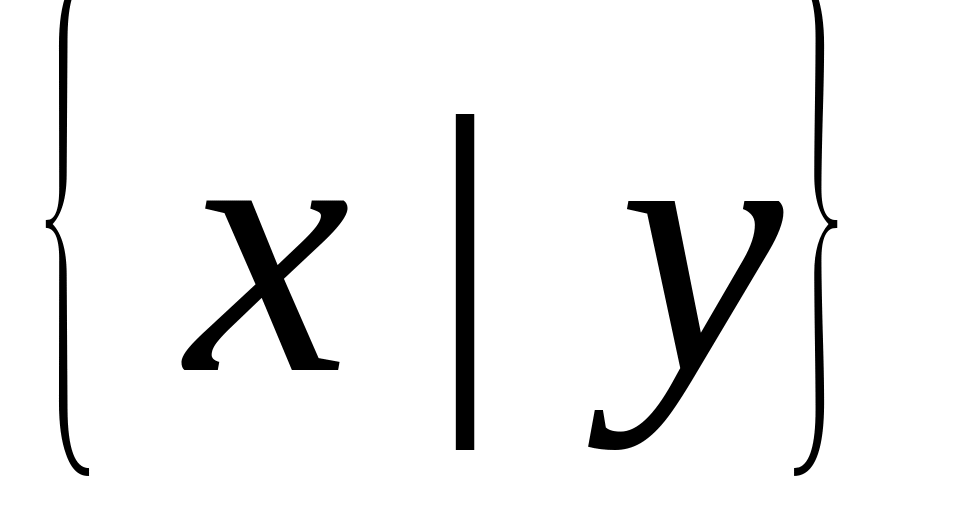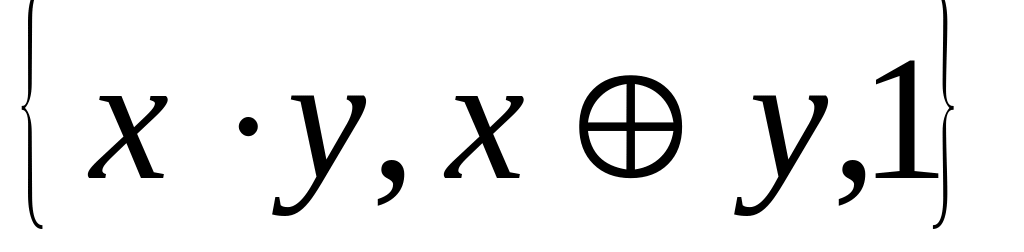
Доведення.

1. Відомо (теорема 1), що система А= 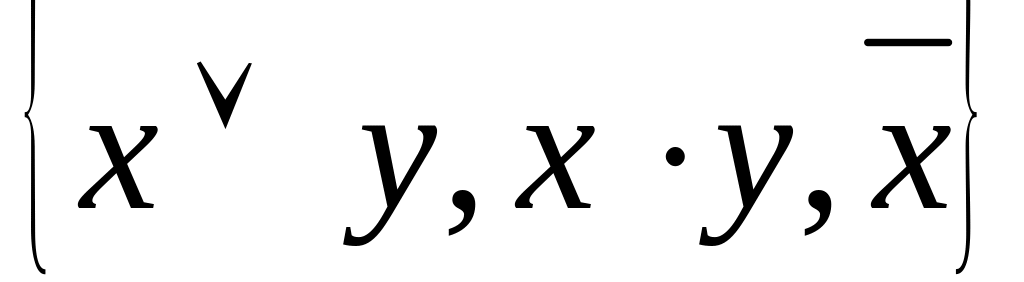повна. Покажемо, що система В= повна. З закону де Моргана 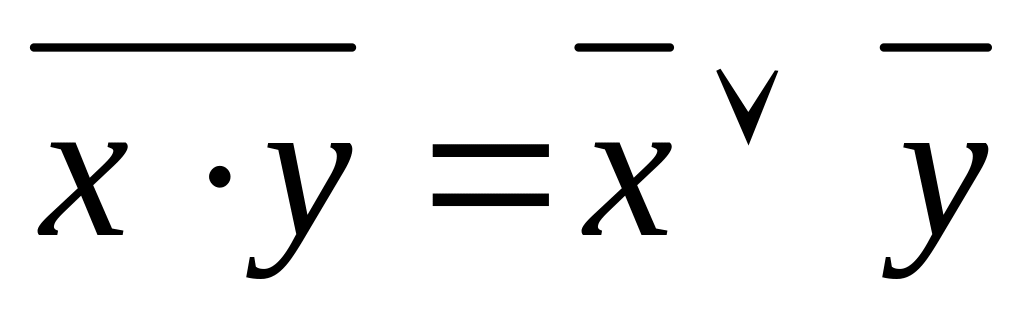отримуємо, що , тобто кон’юнкція виражається через диз’юнкцію і заперечення, і всі функції системи А виражаються формулами над системою В. Система В повна (лема 1).

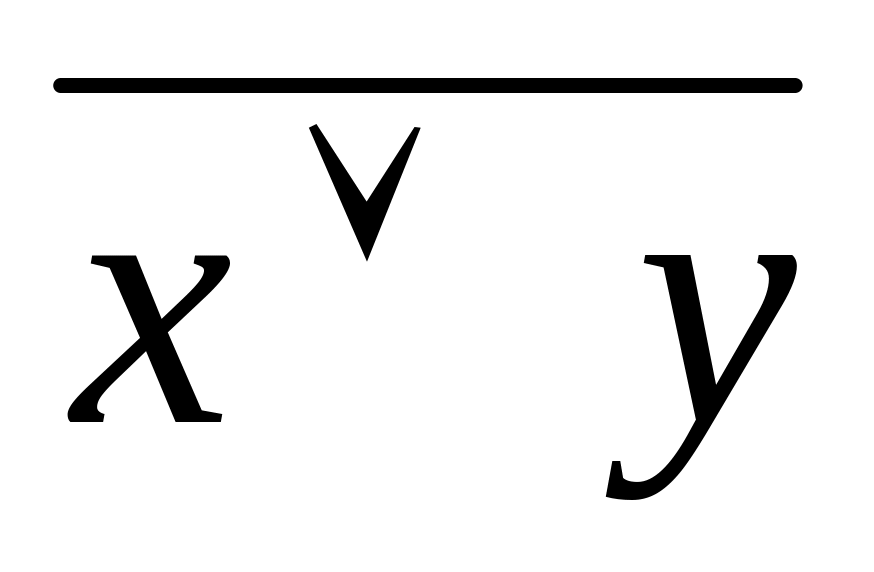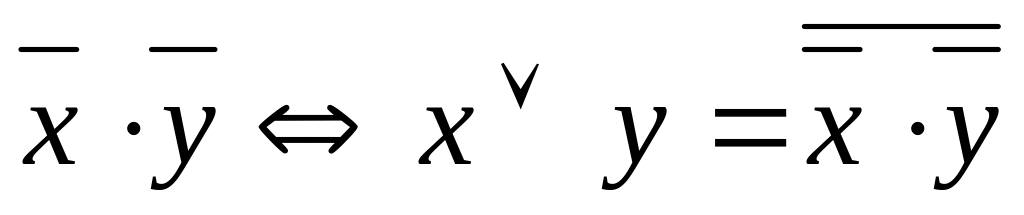2. Аналогічно пункту 1: = із леми 1 випливає, що вираз пункту 2 є правильний.

3. згідно леми 1 система повна.

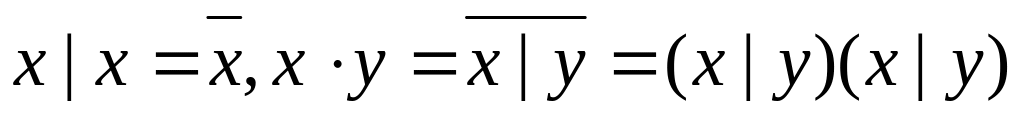4. згідно леми 1 система повна.