3. Тавтології. Класифікація формул алгебри висловлень.

Серед формул алгебри висловлень особливе місце займають ті формули ɑ(A₁,A_2,…,A_n), значення істинності яких при всіх можливих значеннях пропозиційних букв A₁,A_2,…,A_n, дорівнює 1. Іншими словами, значення істинності цих формул при всіх можливих інтерпретаціях дорівнює 1 . Такі формули називаються тавтологіями (тотожно істинними).

Формула логіки висловлень є тавтологією тоді і тільки тоді, коли відповідна функція істинності тотожно дорівнює 1. Тавтології є законами, теоремами логіки висловлень. Те, що формула ɑ є тавтологією, позначають так: ╞ ɑ

Якщо класифікувати всі формули логіки висловлень за значеннями істинності, то крім тавтологій можна виділити класи тотожно хибних формул і нейтральних формул.

Формула логіки висловлень, значення істинності якої дорівнює 0 при всіх можливих значеннях істинності її пропозиційних букв, називається суперечністю або тотожно хибною.

Отже, суперечності - це такі формули, значення істинності яких не дорівнює 1 при жодній інтерпретації.

Формула, яка не є ні тавтологією, ні суперечністю, називається нейтральною.

Будь - яку формулу, яка не є суперечністю називають виконуваною, а не тотожно істинну – спростовною.

Зазначимо, що між формулами різних типів існують певні зв’язки. Зокрема, формула - є тавтологією тоді і тільки тоді, коли ˥ɑ є суперечністю.

Наведемо приклади деяких важливих тавтологій:

П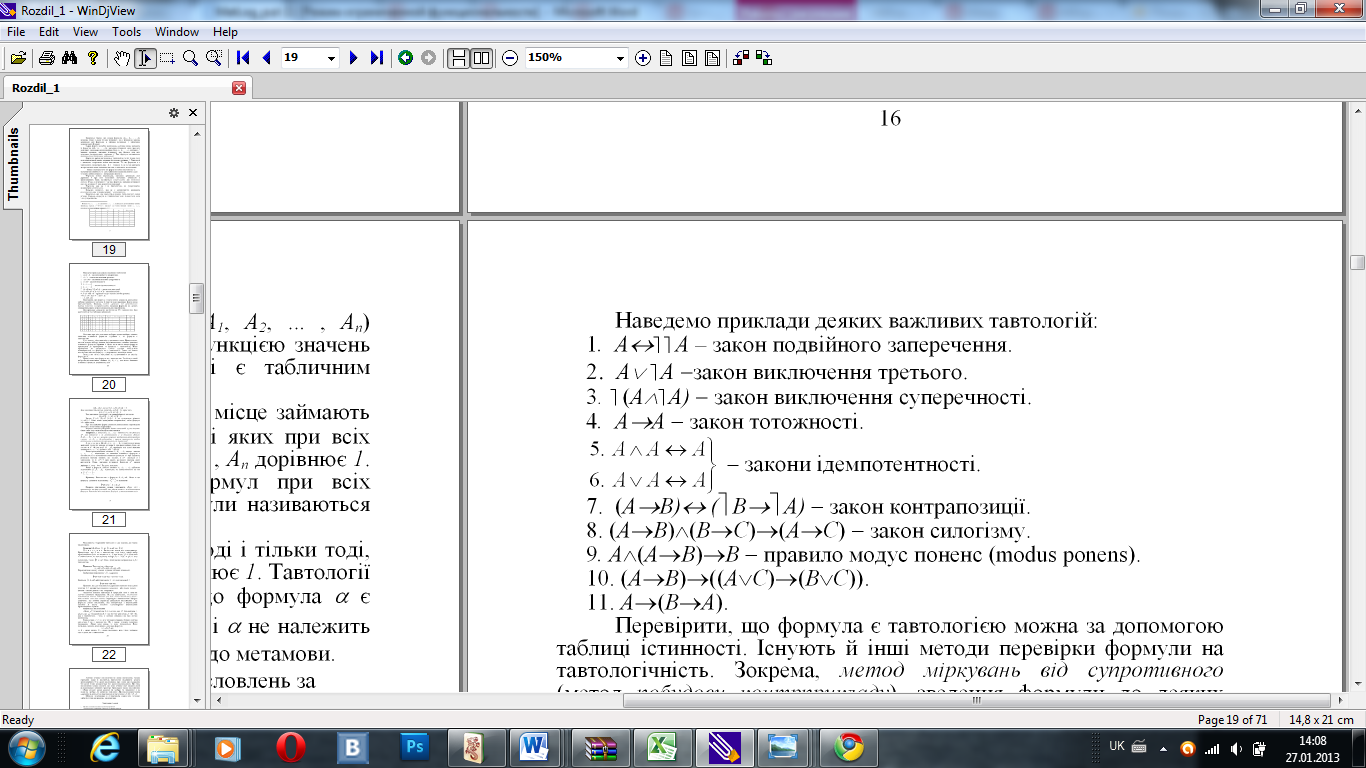 еревірити, що формула є тавтологією можна за допомогою таблиці істинності. Існують й інші методи перевірки формули на тавтологічність. Зокрема, метод міркувань від супротивного (метод побудови контрприкладу ), зведення формули до деяких стандартних форм шляхом рівносильних перетворень.

Для прикладу доведемо, що формула (A→B)→((AᴠC)→(BᴠC) є тавтологією. Для цього побудуємо таблицю істинності:

О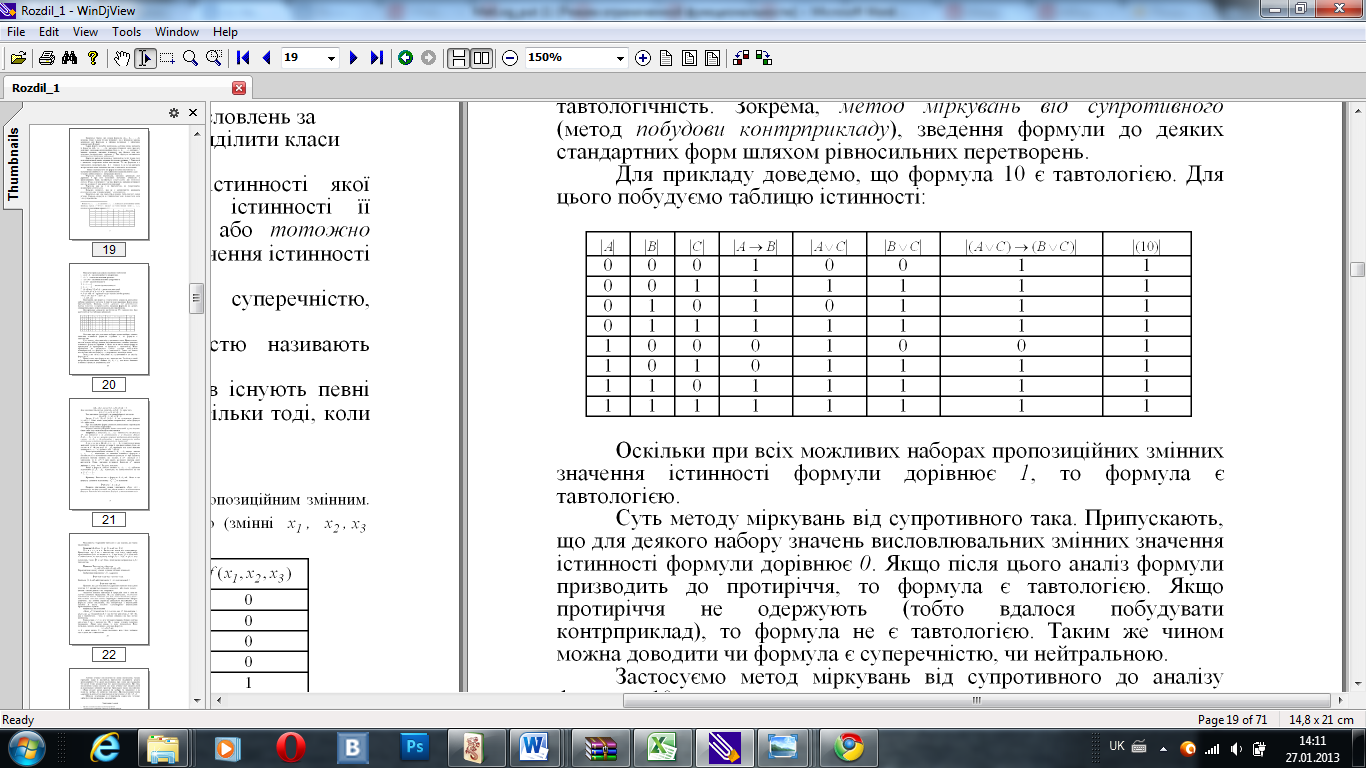 скільки при всіх можливих наборах пропозиційних змінних значення істинності формули дорівнює 1 , то формула є тавтологією.

С уть методу міркувань від супротивного така. Припускають, що для деякого набору значень висловлювальних змінних значення істинності формули дорівнює 0 . Якщо після цього аналіз формули призводить до протиріччя, то формула є тавтологією. Якщо протиріччя не одержують (тобто вдалося побудувати контрприклад), то формула не є тавтологією. Таким же чином можна доводити чи формула є суперечністю, чи нейтральною.

Застосуємо метод міркувань від супротивного до аналізу формули (A→B)→((AᴠC)→(BᴠC).

Припустимо, що формула не є тавтологією. Тоді існує такий набір висловлювальних змінних (A_0, B₀.C₀), для якого значення істинності формули дорівнює нулеві .

Існують способи утворення нових тавтологій з уже відомих. Один з них базується на теоремі підстановки.

Теорема 1.1 . Якщо ɑ(A₁,A_2,…,A_n),– тавтологія, то формула ɑ^* ,яка утворена з ɑ, підстановкою в ɑ довільних формул β₁,β_2,…β_m<=m<=n замість кожного входження пропозиційних змінних A₁,A_2,…,A_n відповідно, є також тавтологія, тобто підстановка в тавтологію призводить до тавтології .

Д о в е д е н н я. Нехай ɑ(A₁,A_2,…,A_n), є тавтологія і задано довільний розподіл значень істинності для пропозиійних букв, які входять в ɑ^*. Формули β₁,β_2,…β_m приймуть тоді деякі значення істинності

x₁ ,x₂,…x_m (кожне х і або 1 , або 0 ).

Якщо пропозиційним змінним A₁,A_2,…,A_n надати значень x₁ ,x₂,…x_m відповідно, то значення істинності формули ɑ збігатиметься із значеннями істинності формули ɑ^*при заданому розподілі значень змінних, які входять в ɑ^*. Оскільки ɑ є тавтологія, то й | ɑ^*| =1 при цьому розподілі значень своїх аргументів. Отже, значення істинності формули ɑ^*завжди дорівнює 1 , тому ╞ ɑ^* .Теорему доведено.

Я кщо в формулі замість змінних A₁,A_2,…,A_n здійснено підстановки β₁,β_2,…β_m відповідно, то записуватимемо це так S _A1,A2,…,An ^{β1,β2,…βm}

Можливість утворювати тавтології з уже відомих дає також така теорема.

Теорема 1.2. Якщо ╞ ɑ і ╞ɑ→β, то ╞β

Д о в е д е н н я. Застосуємо метод від супротивного. Припустимо, що β не є тавтологією, тоді існує такий набір пропозиційних букв, які входять в ɑ і β, при якому | β|=0 . Оскільки ɑ є тавтологією, то при заданому наборі | ɑ | =1 . Тоді | ɑ→β|=0 , а це суперечить умові ╞ɑ→β. Отже, припущення неправильне і β є тавтологією.

Правило, яке дає можливість одержувати тавтології на основі теореми 1.2, називається правилом висновку або modus ponens.

Аналогом поняття тавтології в природній мові є поняття логічно істинного твердження. Як у же зазначалося,

висловлення називається логічно істинним (на базі логіки висловлень) тоді і тільки тоді, коли його логічна структура є тавтологією.

Ще раз зазначимо, що логічна структура складеного висловлення - це формула логіки висловлень, яка утворюється з висловлення заміною в ньому кожного елементарного висловлення пропозиційною буквою. Наприклад, висловлення «Якщо √2 більший ніж 1.4, то з того, що √2 більший ніж 1, слідує, що √2 більший ніж 1.4» має логічну структуру А→ ( В →А ), яка є тавтологією, і тому є логічно істинним на базі логіки висловлень.

Логічно істинне висловлення (в логіці висловлень) можна отримати, якщо в яку-небудь тавтологію підставити замість пропозиційних букв деякі висловлення, при умові, що входження тієї самої букви заміщуються тим самим висловленням. Про таке висловлення можна сказати, що воно істинне вже завдяки своїй функціонально істинній структурі. Прикладом такого висловлення є «Якщо студент склав екзамен на «добре» чи «відмінно», і не склав на «добре», то склав на «відмінно». Це висловлення можна одержати за допомогою підстановки в тавтологію ( АᴠВ ) ^˥В→ А.

Шляхом підстановки в суперечність одержують тотожно хибні (в логіці висловлень) висловлення.