Інтуїтивне поняття алгоритму і необхідність його уточнення.
Алгоритм — це скінченна послідовність однозначних розпоряджень, виконання яких дозволяє за допомогою скінченного числа кроків отримати розв’язання задачі, що однозначно визначається початковими даними. Характеризує алгоритм його зрозумілість для виконавця; детермінованість (визначеність), тобто однозначність результату при заданих початкових даних; дискретність процесу, що визначається алгоритмом, — можливість розчленувати його на окремі елементарні операції, які легко здійснити; масовість — початкові дані, для яких застосуємо алгоритм, можна вибирати з певної множини допустимих значень даних, ця множина може бути як скінченною, так і нескінченною, тобто алгоритм повинен забезпечувати розв’язання будь-якої задачі з певного класу однотипних задач.
Незважаючи на зроблені уточнення поняття алгоритму, ми отримали уявлення про алгоритм в інтуїтивному значенні.
Подані вище коментарі пояснюють інтуїтивне поняття алгоритму, але саме це поняття не стає від цього більш чітким і строгим. Проте математики тривалий час задовольнялися цим поняттям. Лише з виявленням алгоритмічно нерозв’язних задач, тобто задач, для рішення яких неможливо побудувати алгоритм, з’явилася потреба в побудові формального визначення алгоритму, відповідного відомому інтуїтивному поняттю.
Інтуїтивне поняття алгоритму внаслідок своєї розпливчастості не може бути об’єктом математичного вивчення, тому для доказу існування алгоритму розв’язання задачі було необхідне строге формальне визначення алгоритму.
З погляду логічних теорій, алгоритми, призначені для практичних застосувань, є алгоритмами в інтуїтивному значенні.
Отже, ми розглянули інтуїтивне поняття алгоритму.
31. Рекурсивні функції. Основна гіпотеза теорії алгоритмів.
Рекурсією називається такий спосіб організації обробки даних, при якому програма (або функція) викликає сама себе або безпосередньо, або з інших програм (функцій).
Функція називається рекурсивною, якщо під час її обробки виникає її повторний виклик, або безпосередньо, або побічно, шляхом ланцюжка викликів інших функцій.
Рекурсивні функції — клас функцій, введений як уточнення класу обчислюваних функцій. В математиці загальноприйнятою є теза про те, що клас функцій, для обчислення яких існують алгоритми, при найширшому розумінні алгоритму, збігається з класом рекурсивних функцій. У зв'язку з цим, рекурсивні функції грають важливу роль в математиці та її застосуваннях, в першу чергу, в математичній логіці, основах математики та кібернетиці, як ефективно обчислювані функції. Тільки такі функції можна обчислювати на електроних обчислювальних машинах та інших цифрових пристроях.
При введенні класу ефективно обчислюваних функцій природнім чином виникає питання уточнення конструктивних об'єктів, на яких визначено ці функції. Клас всіх таких об'єктів широкий. В той же час, з допомогою методу арифметизації, запропонованого австрійським математиком Куртом Геделем, всі такі об'єкти легко зводяться донатуральних чисел. Тому рекурсивні функції було введено як функції, що визначені на множині натуральних чисел і набувають значення з тієї ж множини натуральних чисел. Перенесення понять і методів вироблених в теорії рекурсивних функцій на функції визначені на складніших конструктивних областях (множини слів деякого алфавіту, формул деякої теорії, графів тощо) не створює принципових ускладнень.
Базовими примітивними функціями, за визначенням, є:
нульова функція
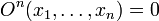
функція слідування
функція проектування
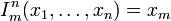
Перед написанням рекурсивних функцій на будь-якій мові програмування, як правило, необхідно записати рекурентне співвідношення, що визначає метод обчислення функцій. Рекурентне співвідношення повинне містити як мінімум дві умови:
I) умова продовження рекурсії (крок рекурсії);
II) умова закінчення рекурсії.
Рекурсію реалізовуватимемо за допомогою виклику функції самої себе. При цьому в тілі функції спочатку слід перевіряти умову закінчення рекурсії. Якщо вона істинна, то виходимо з функції. Інакше здійснюємо рекурсивний крок. Ітеративний варіант функцій реалізовуватимемо за допомогою оператора циклу for.
Основна гіпотеза теорії алгоритмів.
Будь-яка практична задача, що приводить до необхідності створення ефективного обчислювального методу (алгоритму), може бути поставлена в точних математичних термінах.
Ця парадигма (гіпотеза, принцип) стосовно уточнення поняття алгоритм, як абстрактної машини відома, у вигляді тези Т'юринга: «Для всякого алгоритму Sf в якому-небудь алфавіті може бути побудований тьюріноговський алгоритм, що дає при однакових вихідних даних, ті ж самі результати, що і алгоритм Sf».
Прийняття тези Т'юринга рівносильне прийняттю тези Черча (для частково-рекурсивних функції) або принцип нормалізації (для нормальних алгоріфмов).
Всі відомі приклади алгоритмів можна звести до питання обчислення відповідної функції. Вважаючи цю межу алгоритмів основною, можна побудувати формальне уточнення поняття обчислюваної функції. У основі цього твердження лежить теза Черча: “Всяка функція, значення якої може обчислюватися ефективно, є частково-рекурсивною” (тобто обчислюваними функціями є частково-рекурсивні функції – функції, що отримуються за кінцеве число кроків з простих за допомогою суперпозиції, примітивної рекурсії і μ-оператора).
В світлі викладеного в алгоритмічній системі Черча вихідними конструктивними об'єктами є базисні функції (x1, x2.,xm,.,xn)= xm, конструктивний процес обумовлений застосуванням до базисних функцій операторів суперпозиції S, примітивній рекурсії R і мінімізації ?, а результатом кінцевого процесу є рекурсивні функції, тобто:
В даний час широко використовується в теорії алгоритмів теза Черча-Т'юрінга: «Будь-яка теоретично вирішувана обчислювальна задача може бути вирішена за допомогою машини Тюрінга».