20 І 21. Закон двоїстості в логіці предикатів.

Зведені та нормальні форми формул логіки предикатів.

1. Нормальні форми. ˅˄¬

2. Закон двоїстості.

Нормальні форми

У попередній лекції було показано, що для будь-якої пф (у мові { ¬, ˅, ˄, (стрелка в одну сторону, стрелка в две стороны),0,1 }) існує їй рівносильна в мові. {{ ¬, ˅, ˄, 0,1 }. Доведемо, що для

будь-якої пф існує їй рівносильна в мові { ¬, ˅, ˄,}, тобто ця мова теж повна.

Означення 1. Нехай кожне з v1,v2..Vk 0 або 1.

Пф виду

називається елементарною кон 'юнкцією.

Пф виду

називається елементарною диз'юнкцією.

Означення 3. Пф, рівносильна даній і яка має вид

- елементарна кон'юнкція, називається диз'юнктивною нормальною формою (коротко ДНФ) даної пф.

Помітимо, що елементарні кон'юнкції в деякій ДНФ можуть бути і рівними.

Із означення 3 і рівносильності (6) маємо, що ДДНФ пф ^А(X1,^X2,•••,^Xn⁾,

яка містить рівно п різних змінних ^X1,^X2… ^Xn, є її ДНФ, у якій:

1) всі елементарні кон'юнкції попарно різні; 2) кожна елементарна кон'юнкція містить рівно п членів; 3) у кожній елементарній кон'юнкції

зустрічаються всі п змінних ^X1, ^X2,•••, ^Xn («у деяких степенях»).

Теорема 5. Для будь-якої пф існує ДНФ даної пф.

Доведення. Нехай ^А(X1,^X2,•••,^Xn⁾, - довільна пф. Якщо вона є

протиріччям, то в якості її ДНФ, відповідно до рівносильності (15°), візьмемо

Якщо пф ^А(X1,^X2,•••,^Xn⁾,не є протиріччям і містить хоча б одну змінну, то в якості ДНФ візьмемо її ДДНФ; в іншому випадку ця пф -

тавтологія і за ДНФ візьмемо пф Теорему доведено.

Намітимо ще одне доведення теореми 5. Дану пф за рівносильностями (25°) і (21°), застосовуючи їх необхідне число раз, можна перетворити в їй рівносильну, яка не містить символів ^ і якщо вони у ній були. Потім, застосовуючи необхідне число раз рівносильності (1°), (7°), (9°) - (12°), одержуємо ДНФ даної пф.

Більше того, якщо вихідна пф не протиріччя, то можна одержати її ДНФ, яка містить різні елементарні кон’юнкції, в яких одна і та ж змінна не повторюється. Така ДНФ не буде ДДНФ тільки в тому випадку, якщо яка- небудь елементарна кон’юнкція її не містить усіх змінних, що входять у вихідну пф. Але якщо, наприклад, елементарна кон’юнкція

не містить змінної ^Хп, то наступні рівносильні перетворення:

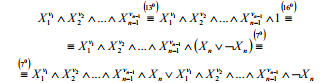
дають дві елементарні кон’юнкції, кожна з яких містить «відсутню» змінну

^Хп. Отже, застосовуючи це перетворення необхідне число раз, із такої ДНФ можна одержати ДДНФ.

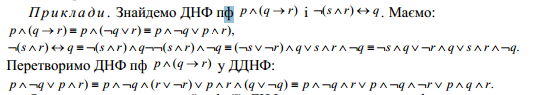Очевидно, що для даної пф її ДНФ не єдина, а для пф, що не є протиріччям і яка містить змінні, її ДДНФ єдина з точністю до перестановки диз'юнктивних членів.

Означення 4. Пф, рівносильна даній і яка має вид

де - елементарна диз'юнкція, називається кон'юнктивною нормальною формою (коротко КНФ) даної пф.

Помітимо, що деяка КНФ може містити рівні елементарні диз'юнкції.

Із означення 4 і рівносильності (11°) маємо, що ДКНФ пф ^А(X1,^X2,•••,^Xn⁾,

яка містить рівно п різних змінних ^Хі,^Х2 … ^Хп, є її КНФ, у якій:

і) всі елементарні диз'юнкції попарно різні; 2) кожна елементарна диз'юнкція містить рівно п членів; з) у кожній елементарній диз'юнкції

зустрічаються всі п змінних ^Х1, ^Х2… ^Хп («у деяких степенях»).

Теорема 6. Для будь-якої пф існує КНФ даної пф.

Доведення. Нехай ^А(X1,^X2,•••,^Xn⁾, - довільна пф. Якщо вона є

тавтологія, то за її КНФ візьмемо пф , що є тавтологією і задовольняє означенню 4. Якщо дана пф не тавтологія і містить хоча б одну змінну, то за КНФ візьмемо її ДКНФ; в іншому випадку ця пф - протиріччя і за КНФ

візьмемо пф . Теорему доведено.

Намітимо ще одне доведення теореми 6. Дану пф за рівносильностями (21°) і (25°), застосовуючи їх необхідне число раз, перетворимо в їй рівносильну, яка не містить символів . Потім, застосовуючи необхідне число раз рівносильності (1°), (8°) - (12°), одержуємо її КНФ.

Більше того, якщо вихідна пф не тавтологія, то можна одержати її КНФ, яка містить різні елементарні кон’юнкції, в яких одна і та ж змінна не повторюється. Така КНФ не буде ДКНФ тільки в тому випадку, якщо яка- небудь елементарна диз'юнкція не містить усіх змінних, що входять у вихідну пф.

Але якщо, наприклад, елементарна диз'юнкція не містить змінної ^Хп, то наступні рівносильні перетворення

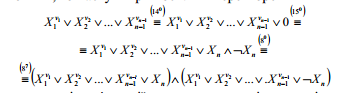
дають дві елементарні диз'юнкції, кожна з яких містить «відсутню» змінну

^Xn. Отже, застосовуючи це перетворення необхідне число раз, із такої КНФ можна одержати ДКНФ.

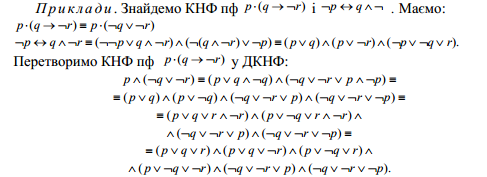
Для даної пф її КНФ не єдина, а для пф яка містить змінні і не є тавтологією, її ДКНФ єдина з точністю до перестановки кон'юнктивних членів.