18. Класифікація формул логіки предикатів. Лзз формули.

Серед формул логіки предикатів особливе місце займають тотожно істинні формули. Формула логіки предикатів називається тотожно істинною або логічно загальнозначущою (скорочено ЛЗЗ), якщо вона істинна в будь - якій інтерпретації. Те, що формула α є ЛЗЗ, позначають ╞α (аналогічно позначалися тавтології). Зазначимо, що всі тавтології логіки висловлень є логічно загальнозначущими формулами (кожна формула логіки висловлень є формулою логіки предикатів).

Очевидно, будь - яка формула логіки предикатів, яка одержується з тавтології шляхом застосування підстановки формул якщо до формули логіки висловлень , яка є тавтологією, застосувати підстановку , де – будь - які формули логіки предикатів, одержимо ЛЗЗ формулу логіки предикатів.

Зазначимо, що формулу, яка одержується підстановкою в тавтологію, називають окремим випадком тавтології . Отже, окремі випадки тавтологій є ЛЗЗ формулами. Так, формула є ЛЗЗ (одержана шляхом застосування підстановки в тавтологію ).

Крім формул, які є окремими випадками тавтологій, є ЛЗЗ формули, які властиві самій логіці предикатів.

Наведемо деякі з них.

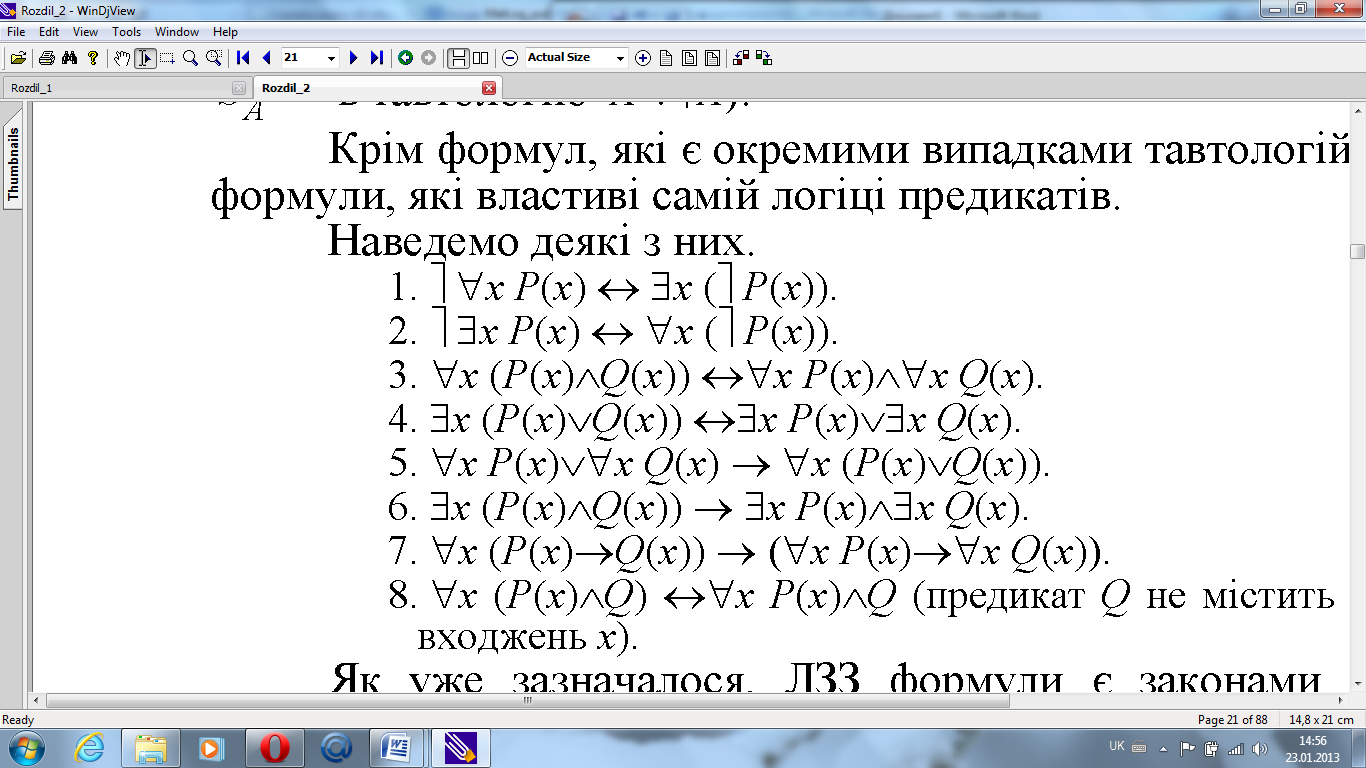
Як уже зазначалося, ЛЗЗ формули є законами логіки.

Зокрема, наведені формули носять назви таких законів :

1, 2 – закони де Моргана для кванторів;

3, 4 – дистрибутивні закони відносно ᴧ і відносно ∨ відповідно;

5 – правосторонній дистрибутивний закон відносно ∨;

6 – лівосторонній дистрибутивний закон відносно;

7 – лівосторонній дистрибутивний закон відносно;

8 – закон пронесення квантора через кон’юнкцію.

Зазначимо, що наведені ЛЗЗ формули 1– 8 можна узагальнити, замінивши атомарні предикати і відповідно довільними формулами і , у яких x –вільна предметна змінна, а Q –будь - якою формулою , яка не містить змінної х .

Для логічно загальнозначущих формул має місце таке твердження: якщо формули α і α→β – логічно загальнозначущі, то формула β також логічно загальнозначуща.

З поняттям логічної загальнозначущості тісно пов’язані питання виконуваності, суперечності формули.

Формула логіки предикатів називається:

1) виконуваною, якщо вона виконувана хоча б в одній інтерпретації;

2) суперечністю (тотожно хибною, невиконуваною), якщо вона хибна в будь - якій інтерпретації;

3) спростовною, якщо вона спростовна хоча б в одній інтерпретації.

Очевидно, має місце наступне твердження:

Формула α – логічно загальнозначуща (суперечна) тоді і тільки тоді, коли ┐α– суперечна (загальнозначуща).

19. Тотожні перетворення логіки предикатів

Для того, щоб мати можливість виконувати тотожні перетво-рення формул логіки предикатів, треба визначити поняття рівно-сильності формул.

Означення. Формуліt а і ß логіки предикатів називаються рівносіаьними або еквівалентнішії, якщо в будь- якій інтерпретації кожне заміщення всіх вільних входжень предметних хитних с а і ß елементами області інтерп/х’тації І) призводить до вислов-лень, які мають ті самі значення істинності.

Якщо формули не містять вільних змінних (замкнені), то означення спрощується. У цьом> разі формули а і ß рівносильні тоді і тільки тоді, коли в будь-якій інтерпретації значення істинності їх однакові.

Відношення рівносильності формул логіки предикатів позначають так само, як і в логіці висловлень, тобто знаком Відношення рівноеильносгі мас властивості рефлексивності, симетричності та транзитивності.

Очевидно, всі рівносильності логіки висловлень мають міспе і в логіці предикатів Крім того, рівносильності формул логіки висловлень є одним із джерел утворення рівносильних формул логіки предикатів Зокрема, окремі випадки рівносильностей формул логіки висловлень (рівносильності. які утворюються з рівносильностей логіки висловлень а(А і. АА ß(A,.A3...,A) шляхом застосування

підстановокS / і і . де Г,. - ДОВІЛЬНІ формули ЛОГІКИ

^л1^/|2 ^и,л*

предикатів) с рівносн.іьносіячи формул логіки предикатів

З означення рівносильності безпосередньо внплпвас , шо a=ß тоді і тільки пнм)і. коли \=a<->ß (формула a<->ß - загаїьнозначуща). Отже, кожну ЛЗЗ формулу, в якої головна операція еквіваленшя, можна записати як рівносн.іьність двох відповідних формул. Інакше кажучи, ця ЛЗЗ формула породжус певну рівносильність.

Наведемо важливі рівносильності формул логіки

предикатів

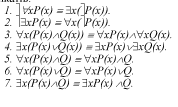
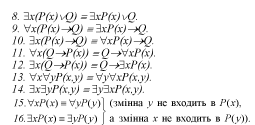
Зазначимо, що ці рівноснльності називають так само, як і відповідні їм ЛЗЗ формули, а саме: 1.2- закони де Моргана для кванторів; 3. 4 - дистрибутивні закони V відносно л і 3 відносно V; 5-12 - пронесення кванторів через кон'юнкцію, диз'юнкцію і імплікацію. 13-14 - закони перестановки однойменних кванторів; 15-16-перейменування предметних змінних

Наведені рівноснльності можна узагальнити, замінивши скрізь атомарні формули Р(х) і О(х) довільними формулами а(х) і ріх)_% в яких предметна змінна .с вільна, а нуль-місний предикатннй символ О -довільною формулою р. яка не містить Змінної х.

Рівносильні формули можугь замінювати одна одну. Внкористову ючн рівноснльності. можна викон\ вати тотожні (рівносильні) перетворення формул логіки преднкагів.

Для формул логіки предикатів, як і для формул логіки висловлень, існують певні стандартні форми. В одних випадках доцільніше користу ватися однією формою, в інших - іншою До стандартних форм формули зводять, застосовуючи рівносильні перетворення. Розглянемо деякі із широковживаних стандартних форм формул логіки предикатів. До таких форм, зокрема, належать такі: зведена випереджена нормальна, сколемівська нормальна. конюнкгнвна нормальна, диз'юнктивна нормальна.

Означення, зведеною формою для формули логіки предикатів називається така рівносильна їй формула; яка не містить інших операцій, крім "1”, "л”, 'V, "V” "З”, причому, якщо вона містить символи заперечення, то вони стосуються ті льки атомарних підформул даної формули.

Означення. Випередженою нормальною формою (ВНФ) для формули логіки предикатів називається така її зведена форма, яка не містить кванторних операцій, або у якої всі кванторні операції винесені наперед.

Теорема. Дія кожної формули логіки предикатів а існує випереджена нормальна форма.

Теорема легко доводиться методом математичної індукції за числом п логічних операцій у формулі.

Якшо n=0. то а - атомарна формула, а. отже, знаходиться у випередженій нормальній формі.

Припустимо, то теорема справедлива для кожної формули яка містить не більше ніж п-1 логічну операцію, і

доведемо ії для формули з n логічними операціями. Для формули а можливі такі чотири випадки: 1) ˥a1 ; 2)а1^а2 : І)a1va2_: 4) Kx1a1, де за припущенням можна вважати, що формули і а1 та a2 подані у випередженій нормальній формі.