
- •Висловлення. Операції над висловленнями.
- •Формули алгебри висловлень. Таблиця істинності формули.
- •Тавтології. Класифікація формул алгебри висловлень.
- •4.Рівносильність формул алгебри висловлень.
- •5.Булеві функції. Питання функціональної повноти.
- •6.Нормальні форми формул алгебри висловлень
- •7. Логічне слідування на базі алгебри висловлень.
- •8. Проблема розв’язуванності в алгебрі висловлень.
- •Метод резолюції в алгебрі висловлень, його застосування.
- •Застосування алгебри висловлень для аналізу і синтезу комбінаційних схем.
- •Зв’язки між формулами алгебри висловлень і формулами числення висловлень.
- •2) Жодне висловлення не є одночасно істинним і хибним (закон виключення суперечності).
- •14.Несуперечність, повнота і розв’язуваність числення висловлень.
- •15. Предикати. Логічні операції над предикатами.
- •Формули логіки предикатів.
- •17. Інтерпретація формул логіки предикатів
- •18. Класифікація формул логіки предикатів. Лзз формули.
- •19. Тотожні перетворення логіки предикатів
- •20 І 21. Закон двоїстості в логіці предикатів.
- •Нормальні форми. ˅˄¬
- •Закон двоїстості.
- •Закон двоїстості
- •22. Логічне слідування в логіці предикатів. Метод резолюції
- •23. Проблема розв’язуванності (вирішення) в логіці предикатів. Теорема Черча.
- •24. Подання знань і одержання виводів за допомогою логіки предикатів
- •25.Застосування логіки предикатів для аналізу міркувань, які виражаються природною мовою.
- •26.Теорії першого порядку. Побудова теорій першого порядку.
- •28. Питання несуперечності, повноти та незалежності аксіом числення предикатів. Проблема розв’язуваності (вирішення) для числення предикатів.
- •29. Формальна арифметика. Питання несуперечності і повноти формальної арифметики. Теореми Геделя, їх філософські аспекти.
- •Інтуїтивне поняття алгоритму і необхідність його уточнення.
- •33.Машини Тьюрінга. Гіпотеза Тьюрінга.
- •Принцип дії
Формули логіки предикатів.
При побудові формул будемо використовувати в основному такі символи:
1) х, у, z, u, v, w, а також ці букви з індексами - для позначення предметних змінних;
2) а, b, c, d, e або ці ж букви з індексами - для позначення предметних констант;
3)
f,
g, h
або ці ж букви з індексами - для позначення
функціональних символів; якщо необхідно
відзначити місткість (кількість
аргументів) функції, то використовуватимемо
верхній індекс. Наприклад, ![]() означатиме n
- місний функціональний символ;
означатиме n
- місний функціональний символ;
4)P,
Q , R, S, T
або ці ж букви з індексами - для позначення
предикатних символів; якщо необхідно
вказати місткість предиката, то
використовуватимемо верхні індекси,
наприклад ![]() (позначення тримісного предиката);
(позначення тримісного предиката);
5)┐,
ᴧ, ∨,
→,
↔,
![]() - для позначення знаків логічних операцій;
- для позначення знаків логічних операцій;
6) круглі дужки і кома – допоміжні.
Спочатку дамо визначення терма:
предметні змінні і предметні константи є термами;
якщо
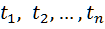 –
терми, а
–
терми, а 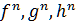 – функціональні символи,
то
– функціональні символи,
то 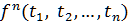 ,
,
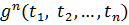 ,
,
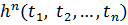 – терми;
– терми;
У логіці висловлень елементарним об’єктом, якому притаманне значення істинності, є атомарне висловлення, яке не можна поділити на компоненти. У логіці предикатів таким елементарним об’єктом, якому притаманне значення істинності, є атомарна формула. Такі формули називають також елементарними. Атомарна формула записується як позначення предиката, за яким в дужках розташовуються аргументи. Кожний аргумент - це терм. Атомарна формула має такий загальний вигляд:
![]() ,
де
,
де ![]() - предикатний символ, а
- предикатний символ, а ![]() - терми. Зокрема,
- терми. Зокрема, ![]() атомарна
формула.
атомарна
формула.
Формули логіки предикатів одержують з атомарних за допомогою знаків логічних операцій. Означення:
1. Атомарна формула є формулою логіки предикатів.
2. Якщо α і β - формули логіки предикатів, то (┐α), (α ᴧ β), (α∨β), (α→β), (α↔β) також формули логіки предикатів.
3.
Якщо α(x)
- формула логіки предикатів, то ![]() і
і ![]() також формули логіки предикатів.
також формули логіки предикатів.
У формули логіки предикатів можуть входити як вільні, так і зв’язані змінні. Формули, які не містять жодної вільної змінної називаються замкненими або реченнями, а ті, що містять вільні предметні змінні, називаються відкритими.
Зазначимо,
що при різноманітних перетвореннях
формул часто користуються підстановками
термів замість вільних змінних. змінних.
Наприклад, результатом підстановки у
формулу ![]() терма f(u)
замість y
терма f(u)
замість y
![]() є формула
є формула ![]()
Проте
не кожний терм можна підставлят и замість
вільної змінної. Наприклад, якщо P(u
, v)
інтерпретувати як «u
= v»,
то формула![]() ,
де
,
де ![]() ,
для будь - якого фіксованого у
є істинним висловленням. Якщо здійснити
підстановку
,
для будь - якого фіксованого у
є істинним висловленням. Якщо здійснити
підстановку ![]() ,
то дістаємо тотожно хибне висловлення
,
то дістаємо тотожно хибне висловлення
![]() .
Отже, неможна здійснювати підстановку,
в результаті якої вільна змінна, замість
якої підставляється терм, перетворюється
на зв’язану.
.
Отже, неможна здійснювати підстановку,
в результаті якої вільна змінна, замість
якої підставляється терм, перетворюється
на зв’язану.
Означення.
Терм
t
називається допустимим для підстановки
у формулу α(x)
замість x
(або вільним для змінної в α(x)),
якщо жодне вільне входження x
в α
не знаходиться в області дії ніякого
квантора ![]() y
або
y,
де y
– змінна, яка входить в t.
y
або
y,
де y
– змінна, яка входить в t.
17. Інтерпретація формул логіки предикатів
Я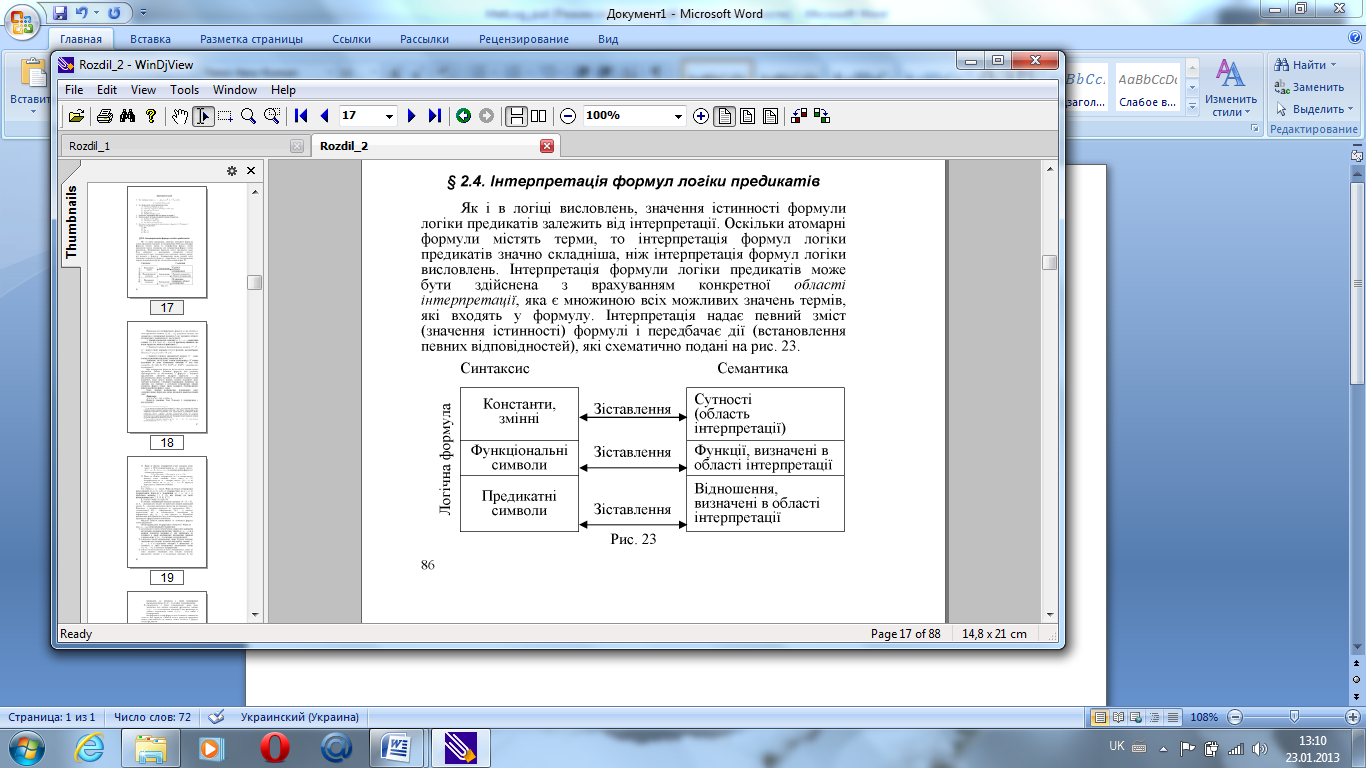 к
і в логіці висловлень, значення істинності
формули логіки предикатів залежить від
інтерпретації. Оскільки атомарні формули
містять терми, то інтерпретація формул
логіки предикатів значно складніша,
ніж інтерпретація формул логіки
висловлень. Інтерпретація формули
логіки предикатів може бути здійснена
з врахуванням конкретної області
інтерпретації , яка є множиною всіх
можливих значень термів, які входять у
формулу. Інтерпретація надає певний
зміст (значення істинності) формулі і
передбачає дії (встановлення певних
відповідностей), які схематично подані
на рис.23
к
і в логіці висловлень, значення істинності
формули логіки предикатів залежить від
інтерпретації. Оскільки атомарні формули
містять терми, то інтерпретація формул
логіки предикатів значно складніша,
ніж інтерпретація формул логіки
висловлень. Інтерпретація формули
логіки предикатів може бути здійснена
з врахуванням конкретної області
інтерпретації , яка є множиною всіх
можливих значень термів, які входять у
формулу. Інтерпретація надає певний
зміст (значення істинності) формулі і
передбачає дії (встановлення певних
відповідностей), які схематично подані
на рис.23
Формально
під інтерпретацією формули α,
яка містить n
- місні предикатні символи ![]() ,
,![]() ,…,
,…,![]() ,
розуміють систему, яка складається з
не порожньої множини D,
яку називають областю інтерпретації,
і відповідності I
, яка зіставляє:
,
розуміють систему, яка складається з
не порожньої множини D,
яку називають областю інтерпретації,
і відповідності I
, яка зіставляє:
Кожній предметній константі а,b,…, e - конкретний елемент з D, (т.б. I (а), I (b),…, I (e)
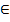 D);
при цьому вважають, що вільні предметні
змінні в α пробігають D* .
D);
при цьому вважають, що вільні предметні
змінні в α пробігають D* .Кожному k- місному функціональному символу
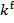 ,
, 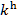 ,
,
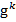 - певну k - місну операцію в D (т.б. функцію,
яка відображає
- певну k - місну операцію в D (т.б. функцію,
яка відображає 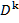 в D ; I (
) ,I
в D ; I (
) ,I 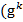 ),
I (
)
:
),
I (
)
:
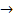 D ) ** .
D ) ** .Кожному n - місному предикатному символу
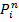 -
деяке n
- місне відношення (предикат), визначене
на
-
деяке n
- місне відношення (предикат), визначене
на 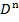 .
.
Зазначимо,
що будь - яке n-
місне відношення в
можна розглядати як деяку підмножину
множини
всіх n-ок
елементів з D,
тобто I(
)
![]() (
),
(
)
- множина всіх підмножин
.
(
),
(
)
- множина всіх підмножин
.
При інтерпретації формули, які не містять жодної вільної предметної змінної (замкнені формули або речення), перетворюються на висловлення, а формули з вільними предметними змінни ми (відкриті формули) - на висловлювальну форму. Істинність чи хибність останніх можна визначити, якщо замість вільних змінних підставити деякі значення (елементи) з множини інтерпретації. Зазначимо, що значення, які отримані в результаті інтерпретації виразів (символів, формул тощо), також називають інтерпретаціями виразів (символів, формул тощо).
Отже, завдяки встановлення відповідності через «інтерпретацію» формулам логіки предикатів надається певний зміст.
Введемо поняття виконуваності та істинності формул логіки предикатів.
Нехай
задана деяка інтерпретація з областю
D
. Формула ![]() логіки предикатів називається :
логіки предикатів називається :
1)
виконуваною
в даній інтерпретації,
якщо існує заміщення всіх вільних
входжень предметних змінних ![]() в
в ![]() назвами елементів множини D,
яке призводить до істинного в даній
інтерпретації висловлення (іншими
словами, якщо
назвами елементів множини D,
яке призводить до істинного в даній
інтерпретації висловлення (іншими
словами, якщо ![]() істинне в інтерпретації) ;
істинне в інтерпретації) ;
2)
істинною
в даній інтерпретації
, якщо будь - яке можливе заміщення всіх
вільних входжень предметних змінних
![]() в
елементами множини D
призводить до істинного в даній
інтерпретації висловлення (якщо
в
елементами множини D
призводить до істинного в даній
інтерпретації висловлення (якщо ![]() в
істинне в інтерпретації) ;
в
істинне в інтерпретації) ;
3) хибною (невиконуваною) в даній інтерпретації, якщо не існує жодного заміщення всіх вільних входжень предметних змінних в елементами множини D , яке призводить до істинного в даній інтерпретації висловлення (якщо хибне в інтерпретації) ;
4)
спростовною в даній інтерпретації, якщо
існує заміщення всіх вільних входжень
предметних змінних
в
елементами множини D, яке призводить до
хибного висловлення (якщо ![]() хибне в інтерпретації).
хибне в інтерпретації).
Інтерпретація, в якій формула стає істинною, називається моделлю цієї формули. Поняття моделі формули природним чином узагальнюється до поняття моделі множини Г формул логіки предикатів.
Інтерпретація називається моделлю множини формул Г, якщо кожна формула з Г істинна в цій інтерпретації.
