1. Висловлення. Операції над висловленнями.

Висловленням називатимемо речення, про яке можна сказати, істинне воно (його зміст) чи хибне. Звичайно, це не означення, а роз’яснення. Означення поняття висловлення не можна дати, оскільки воно належить до основних понять.

У логіці висловлень 1) висловлення розглядаються лише з точки зору їх істинності або хибності; ніякими іншими властивостями висловлень не цікавляться; 2) значення істинності чи хибності висловлень не аналізується, а береться як дані. Відповідь про істинність чи хибність висловлення дає та галузь науки чи людської діяльності, до якої воно належить. Розглянемо приклади:

1) Термін «логіка» походить від грецького слова що означає «слово», «думка», «міркування», «закономірність», і використовується для позначення як сукупності правил, яким підпорядковується процес мислення, так і науки про правила міркування і тих формах, в яких воно здійснюється;

2) 10 ділиться на 2 ;

3) 3 більше 5 ;

4) Кожний ромб є паралелограм;

5) Сьогодні 20 червня;

6) Х+У=1 ;

7) Для кожного цілого числа X існує таке ціле число Y , що Х+У=1 ;

8) Опрацюйте матеріал першого розділу.

Речення 1 - 5, 7 є висловленнями, причому 1, 2, 4, 7 – істинні, висловлення 3 - хибне. Істинність і хибність зазначених висловлень має абсолютний характер. П`яте висловлення істинне лише один раз на рік (істинність його має відносний характер). Речення 6 і 8 не є висловленнями.

У подальшому дотримуватимемось точки зору двозначної класичної логіки, в якій приймаються два основних припущення:

1) кожне висловлення є або істинним, або хибним, тобто третього не дано (закон виключення третього);

2) жодне висловлення не є одночасно істинним і хибним (закон виключення суперечності).

Існують й інші напрями сучасної символічної логіки, в яких зазначені закони можуть і не мати місця. Наприклад, у тризначній логіці Я.Лукасевича висловлення може бути істинним ( 1 ), хибним ( 0 ), нейтральним ( 1\2).

Висловлення позначатимемо великими латинськими буквами A,B,C (з індексами чи без них), які називатимемо пропозиційними буквами або пропозиційними змінними, або висловлювальними змінними . Домовимось записувати ǀAǀ=1, якщо висловлення A – істинне, і ǀAǀ=0, якщо хибне. У першому випадку говорять, що значення істинності висловлення A (значення функції істинності для даного значення аргументу) дорівнює 1, а в другому, що значення істинності висловлення A дорівнює 0 .

Висловлення бувають простими і складеними . Складені висловлення утворюються з простих за допомогою логічних зв’язок (операцій). Розглядатимемо тільки істинностно - функціональні комбінації висловлень, в яких істинність чи хибність нових висловлень однозначно визначається істинністю чи хибністю складових. Очевидно, що

ǀφ(A₁,A₂….,A_n)ǀ= f(ǀA₁ǀ,ǀA₂ǀ….,ǀA_nǀ).

де φ(A₁,A₂….,A_n) - складене з A₁,A₂….,A_n висловлення, f – функція від n аргументів. Особливістю функції f є те, що її значення, як і значення її аргументів належать множині {0;1}. Такі функції називаються булевими функціями. Взагалі булева функція від n аргументів визначається як відображення множини {0;1}ⁿ на {0;1}.

Розглянемо основні логічні операції, за допомогою яких з простих висловлень будують складені висловлення.

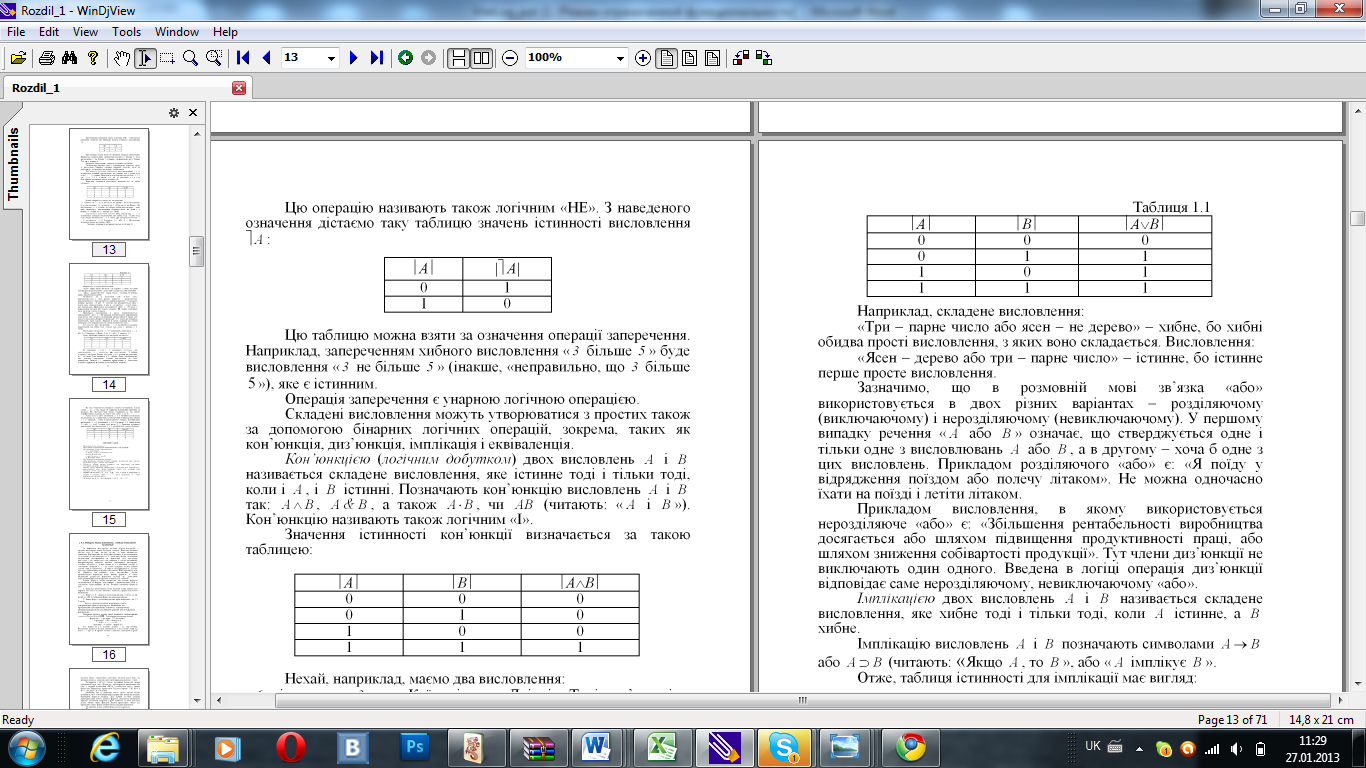Запереченням висловлення A називається таке висловлення, яке істинне, коли A хибне, і хибне, коли A істинне. Заперечення висловлення A позначають через ˥ A або A (читають: «не A »).

Цю операцію називають також логічним «НЕ».

Наприклад, запереченням хибного висловлення « 3 більше 5 » буде висловлення « 3 не більше 5 » (інакше, «неправильно, що 3 більше 5 »), яке є істинним.

Операція заперечення є унарною логічною операцією.

Складені висловлення можуть утворюватися з простих також за допомогою бінарних логічних о перацій, зокрема, таких як кон’юнкція, диз’юнкція, імплікація і еквіваленція.

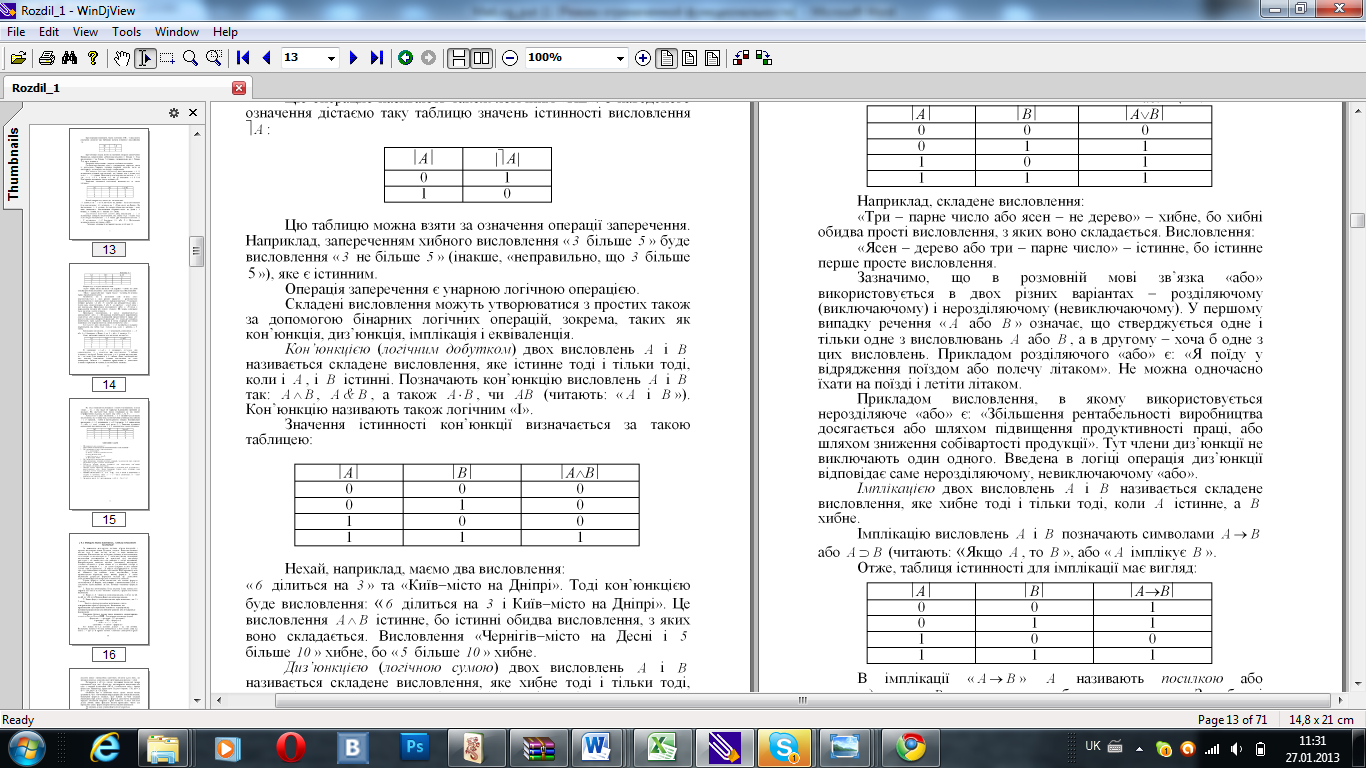Кон’юнкцією ( логічним добутком ) двох висловлень A i B називається складене висловлення, яке істинне тоді і тільки тоді, коли і A, і B істинні. Позначають кон’юнкцію висловлень A і B так: A^B, A&B, A●B, чи AB(читають: «A і B»). Кон’юнкцію називають також логічним «І».

Нехай, наприклад, маємо два висловлення: « 6 ділиться на 3 » та «Київ місто на Дніпрі». Тоді кон’юнкцією буде висловлення: « 6 ділиться на 3 і Київ місто на Дніпрі». Це висловлення A^B істинне, бо істинні обидва висловлення, з яких воно складається. Висловлення «Чернігів місто на Десні і 5 більше 10 » хибне, бо « 5 більше 10 » хибне.

Диз’юнкцією ( логічною сумою ) двох висловлень A і B називається складене висловлення, яке хибне тоді і тільки тоді, коли обидва висловлення A і B хибні. Диз’юнкцію висловлень A і B позначають AᴠB (читають: « A або B »). Диз’юнкцію називають також логічним «АБО».

Наприклад, складене висловлення: «Три - парне число або ясен -не дерево» - хибне, бо хибні обидва прості висловлення, з яких воно складається. Висловлення: «Ясен - дерево або три - парне число» - істинне, бо істинне перше просте висловлення.

Зазначимо, що в розмовній мові зв’язка «або» використовується в двох різних варіантах - розділяючому (виключаючому) і нерозділяючому (невиключаючому). У першому випадку речення « A або B » означає, що стверджується одне і тільки одне з висловлювань A або B , а в другому - хоча б одне з цих висловлень. Прикладом розділяючого «або» є: «Я поїду у відрядження поїздом або полечу літаком». Не можна одночасно їхати на поїзді і летіти літаком.

Прикладом висловлення, в якому використовується нерозділяюче «або» є: «Збільшення рентабельності виробництва досягається або шляхом підвищення продуктивності праці, або шляхом зниження собівартості продукції». Тут члени диз’юнкції не виключають один одного. Введена в логіці операція диз’юнкції відповідає саме нерозділяючому, невиключаючому «або».

І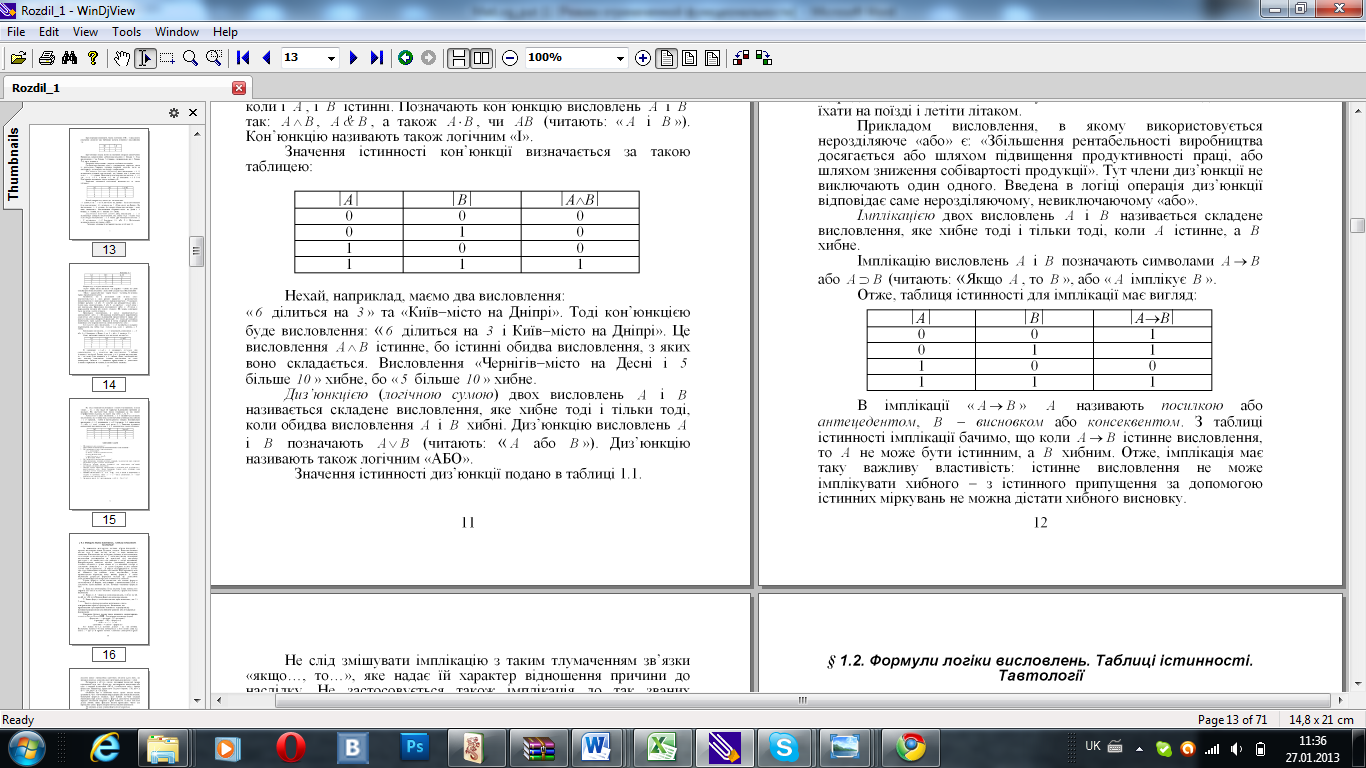 мплікацією двох висловлень A і B називається складене висловлення, яке хибне тоді і тільки тоді, коли A істинне, а B хибне. Імплікацію висловлень A і B позначають символами A→B або A ↄ B (читають:« Якщо A , то B», або «A імплікує B ».

В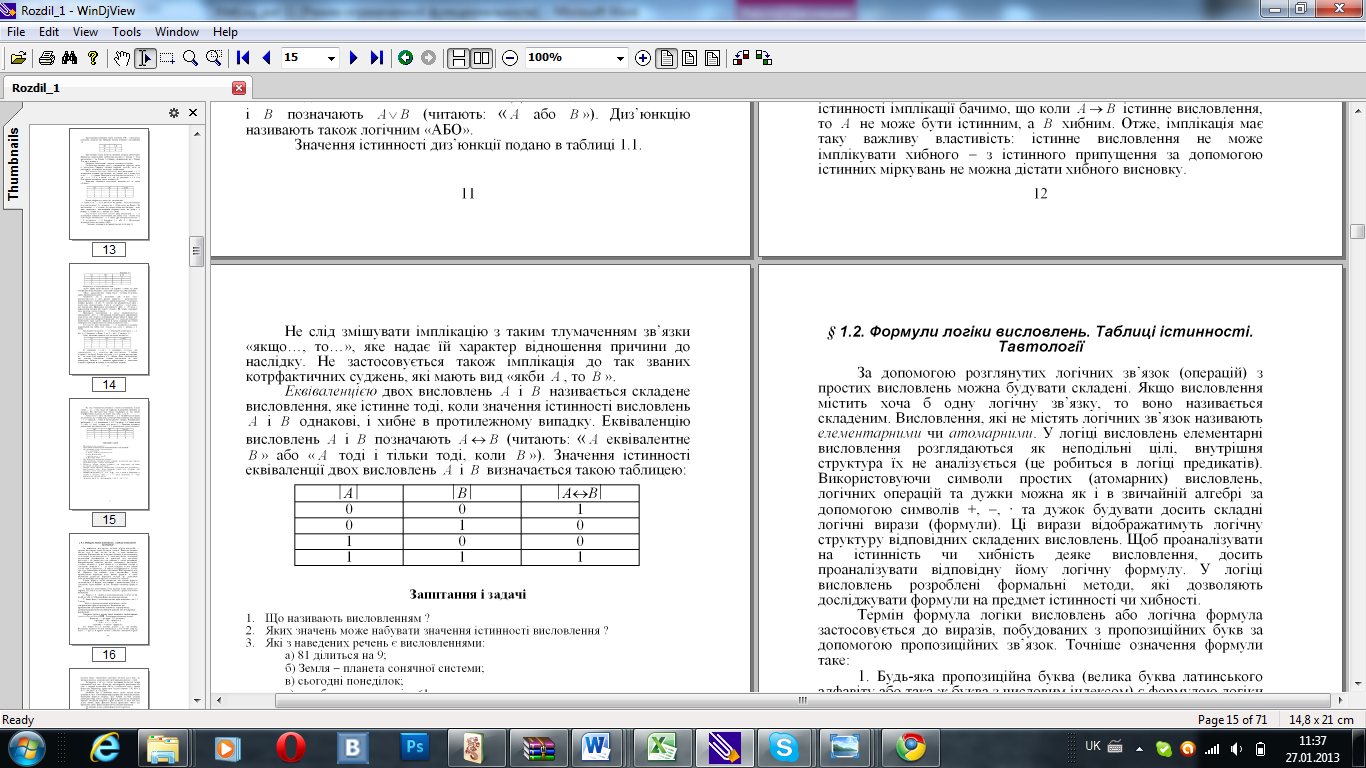 імплікації «A→B» A називають посилкою або антецедентом , B - висновком або консеквентом . З таблиці істинності імплікації бачимо, що коли A→B істинне висловлення, то A не може бути істинним, а B хибним. Отже, імплікація має таку важливу властивість: істинне висловлення не може імплікувати хибного - з істинного припущення за допомогою істинних міркувань не можна дістати хибного висновку. Не слід змішувати імплікацію з таким тлумаченням зв’язки «якщо…, то…», яке надає їй характер відношення причини до наслідку. Не застосовується також імплікація до так званих котрфактичних суджень, які мають вид «якби A, то B ».

Еквіваленцією двох висловлень A і B називається складене висловлення, яке істинне тоді, коли значення істинності висловлень A і B однакові, і хибне в протилежному випадку. Еквіваленцію висловлень A і B позначають A↔B (читають: « A еквівалентне B » або « A тоді і тільки тоді, коли B »).