4.2. Майбутня та поточна вартість фінансових інструментів

Для прийняття осмислених Інвестиційних рішень часто ви­никає необхідність проведення порівняльного аналізу ефек­тивності різних напрямів вкладання коштів у ті чи інші фінан­сові інструменти. Такий аналіз пов'язаний із процесом наро­щування вартості грошових ресурсів і процесом дисконтуван­ня Їх вартості.

Вартість певної суми грошей - це функція від часу виник­нення грошових доходів чи витрат. Принцип вартості грошей у часі базується на тому, що сьогодні грошова одиниця коштує більше, ніж у майбутньому. Цей принцип діє незалежно від зміни загального рівня цін.

Нарощування - метод зведення реальної вартості коштів до їх вартості в майбутньому періоді, що використовується для оцінки майбутньої вартості використовується для оцінки майбутньої вартості інвестицій.

Дисконтування - метод приведення майбутньої вар­тості коштів до їх вартості в поточному періоді (до реальної вартості грошей).

Таким чином, розрізняють:

- майбутню вартість — надходження, що перебувають за межами сьогоднішнього дня;

- поточну вартість — зведена до сьогоднішнього моменту величина, яка буде отримана або оплачена в певний момент у майбутньому.

Одиничний грошовий потік, — сума, що виплачується одно­разово.

Ануїтет — рівномірні грошові потоки, що регулярно над­ходять:

-звичайний ануїтет — рівномірні грошові потоки, що про­водяться в кінці періоду:

-серія рівномірних платежів - платежі, що вносяться чи одер­жуються через рівні проміжки часу на початку певного періоду.

Під час проведення фінансово-економічних розрахунків, по­в'язаних з інвестуванням коштів, процеси нарощування і дисконтування вартості можуть здійснюватись як за простими, так і за складними процентами. Прості проценти застосовують­ся, як правило, при короткостроковому інвестуванні, складні — при довгостроковому.

Рис. 4.1. Поьочна вартість та грошові потоки

Основне положення при вимірюванні вартості коштів у часі полягає в тому, що поточний час або поточний період є пері­од часу нуль – t0. Оплата або надходження, зроблені в період один від поточного часу, прийнятого за нуль, t1 розглядають­ся як зроблені в період часу один (t1), у період часу два (t2). Це положення можна подати у вигляді такої часової лінії:

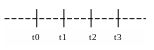
Рис. 4.2. Періоди надходження або утворення доходів

Ця умова значно спрощує визначення періоду часу. Визначення вартості грошей у часі необхідне, щоб підсумову­вати грошові потоки, які надходять у різні періоди часу.

Рис. 4.3. Схема визначення поточної вартості фінансових інструментів.

Простим процентом називається сума, яка нараховується за початковою (реальною) вартістю вкладу в кінці одного періоду платежу, що визначається умовами інвестування коштів (місяць, квартал і т. п.). Розрахунок суми простого процента в процесі нарощування вкладу такий:

J=P*n*Z

де J — сума процента за обумовлений період Інвестування в цілому; Р - початкова сума вкладу (інвестицій); п - тривалість інвестування (кількість періодів); Z— процентна ставка у віднос­них величинах.

У цьому разі майбутня вартість вкладу (У) разом із нарахова­ною сумою процента визначається за формулою:

S=P+J=P(1+nZ)

Множник (1+nZ) називається коефіцієнтом нарощування прос­тих процентів. Його значення завжди має бути більше за одиницю.

При розрахунку суми простого процента в процесі дискон­тування вартості коштів (тобто суми дисконту) використовується така формула:

(4.1)

де D — сума дисконту (за простими процентами) за обумовле­ний період інвестування в цілому; S — кінцева сума вкладу, що залежить від умов інвестування; п - тривалість інвестування (кількість періодів); Z — використовувана дисконтна ставка у відносних величинах.

У цьому разі реальна вартість грошових ресурсів (Р) з ураху­ванням розрахованої суми дисконту визначається так:

(4.2)

Множник 1/(1+nZ) називається дисконтним множником (коефіцієнтом) простих відсотків, значення якого завжди має бути меншим за одиницю.

Складним відсотком називається сума прибутку, яка утво­рюється в результаті інвестування за умови, що сума нарахова­ного відсотка (простого) не виплачується після кожного періоду, а додається до суми основного внеску і в наступному періоді платежу сама дає прибуток. При розрахунку суми внеску в про­цесі його нарощування за складними відсотками (Sс) використо­вується формула:

(4.3)

Відповідно сума відсотка (Jс) у цьому разі становить:

Jc=Sc-P (10.6)

При розрахунку реальної вартості коштів у процесі дискон­тування за складними відсотками (Рс) використовується така формула:

(4.4)

Відповідно сума дисконту (Ос) у цьому разі дорівнює:

Dс=S-Рс. (4.5)

Множники (1+Z)ⁿ і 1/(1+Z)ⁿ називаються відповідно множ­ником нарощування і множником дисконтування складних відсотків.

Якщо інвестиції дають прибуток, який надходить у вигляді серії декількох однакових за розміром виплат протягом рівних проміжків часу, така серія виплат називається ануїтетом. Кож­на виплата в межах ануїтету може бути знову інвестована з тим, щоб на неї нараховувалися складні відсотки. Тому май­бутня вартість ануїтету (Sа), що дає протягом п років щорічні виплати прибутку D в умовах, коли на ці виплати згодом на­раховується процент Z, складається із сукупності кожної ви­плати за ануїтетом;

(4.6)

де Кsa — коефіцієнт майбутньої вартості ануїтету (множник ануїтету).

Виходячи з цього, реальна вартість ануїтету заснована на виплаті п разів серії рівномірних платежів:

(4.7)

де Kpa - коефіцієнт реальної вартості ануїтету (дисконтний множник ануїтету).

Використовуючи наведені вище рівняння (формули), можна скласти моделі, що дають змогу оцінювати вартість різних видів цінних паперів та фінансових інструментів.