
- •Глава 2.Числовые последовательности и их свойства §3.Числовые последовательности
- •12.Основные определения
- •13.Способы задания последовательностей
- •14.Монотонность числовых последовательностей
- •15.Ограниченность числовых последовательностей
- •§4.Сходящиеся последовательности и их свойства
- •12.Основные определения
- •13.Свойства сходящихся последовательностей
- •14.Аксиома Больцано-Вейерштрасса и теорема о стягивающейся системе отрезков
- •15.Вычисление пределов сходящихся числовых последовательностей
- •§5.Замечательные пределы
- •12.Сложные проценты
- •13.Число
- •14.Вычисление пределов, связанных с числом
- •§6.Бесконечно малые последовательности и их свойства
- •12.Определение и примеры бесконечно малых последовательностей
- •13.Свойства бесконечно малых последовательностей
- •14.Применение бесконечно малых последовательностей к доказательству теорем о пределах
- •§7.Бесконечно большие последовательности
- •12.Определение и примеры
- •13.Связь между бесконечно большими и неограниченными последовательностями
- •14.Связь между бесконечно большими и бесконечно малыми последовательностями
- •Упражнения к
13.Свойства сходящихся последовательностей
Если последовательность сходится, то она имеет только один предел.
пусть
 и
и
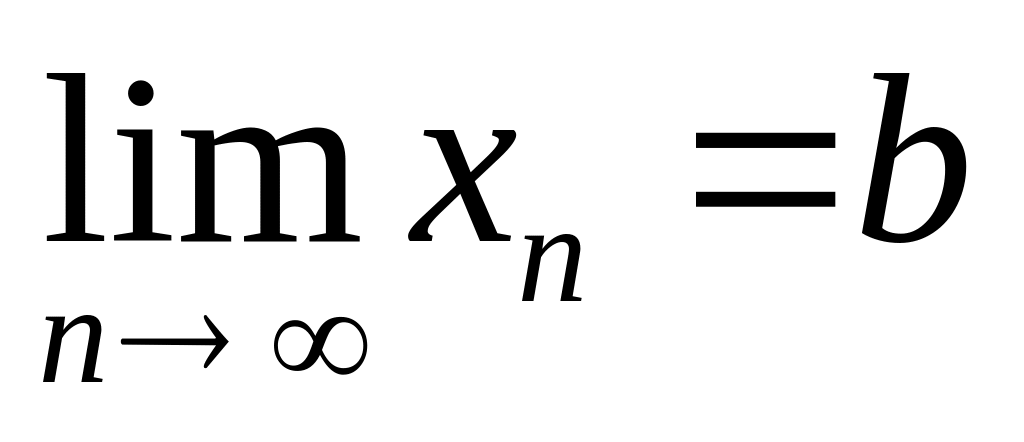 ,
где
,
где
 ,тогда
для любого положительного числа
найдется натуральное число
,тогда
для любого положительного числа
найдется натуральное число
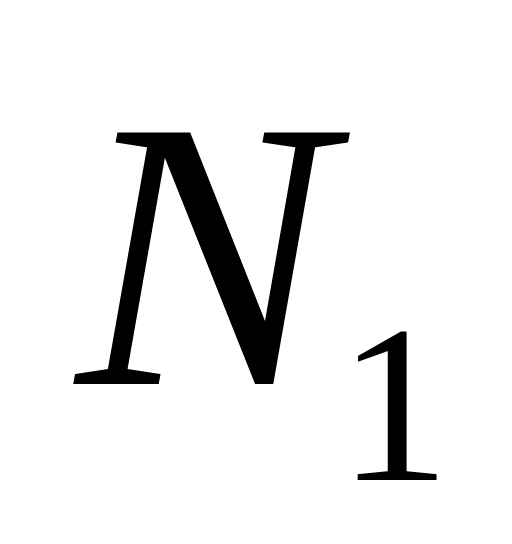 такое, что для
такое, что для
 и найдется такое натуральное число
и найдется такое натуральное число
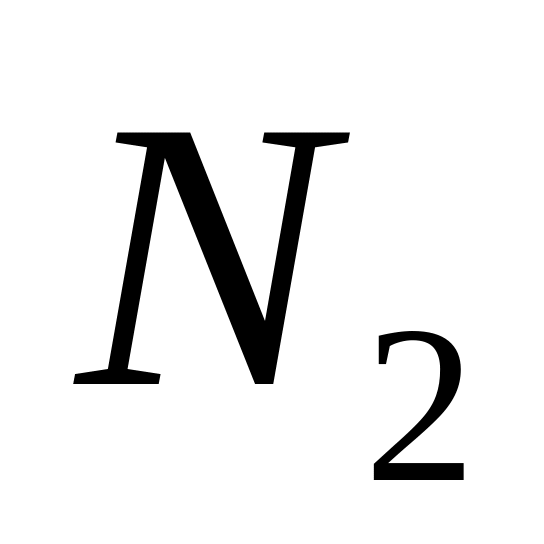 ,
что для
,
что для
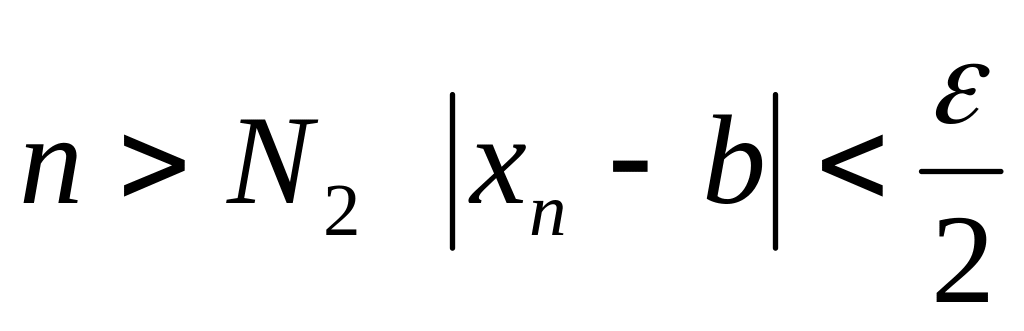 .
.
Возьмем
![]() ,
тогда имеем:
,
тогда имеем:
![]() и
и
![]() ,
следовательно
,
следовательно
![]() .
.
![]() ,
но
- любое сколь угодно малое положительное
число Значит,
,
но
- любое сколь угодно малое положительное
число Значит,
![]() .
Полученное противоречие доказывает
теорему.
.
Полученное противоречие доказывает
теорему.
Если последовательность сходится, то она ограничена.
пусть
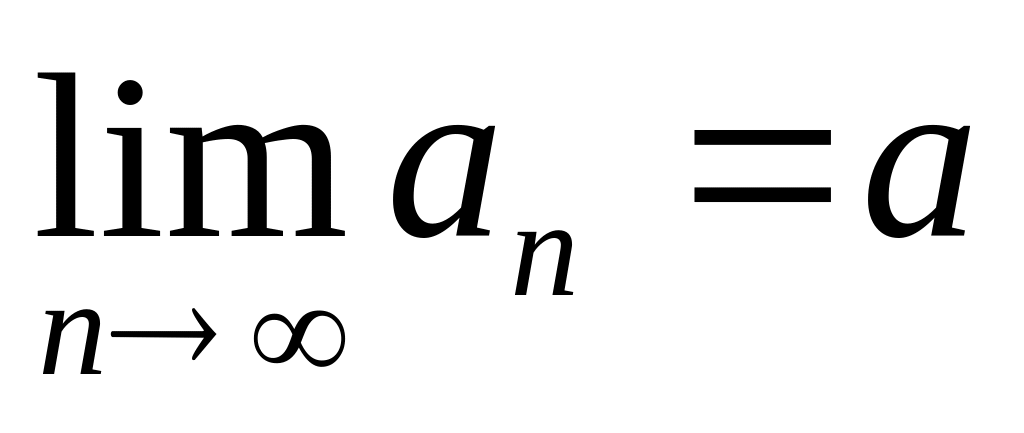 ,
тогда
,
тогда
 и
и
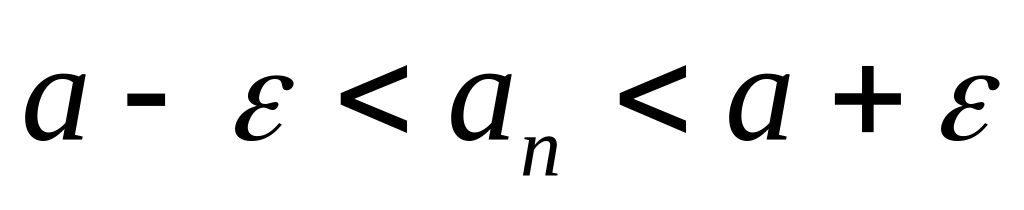 .
Если в качестве
выбрать
.
Если в качестве
выбрать
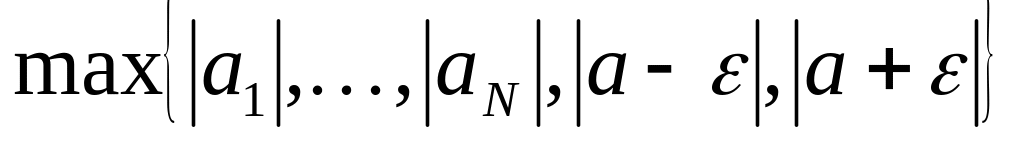 ,
то
,
то
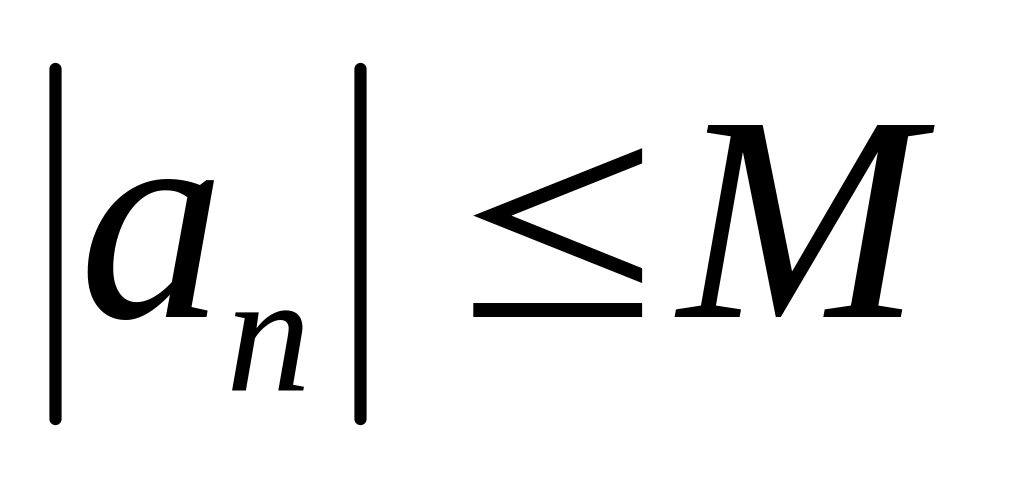 .Обратное
утверждение неверно, например
.
Эта последовательность ограничена, но
не имеет предела.
.Обратное
утверждение неверно, например
.
Эта последовательность ограничена, но
не имеет предела.
(«о двух милиционерах»). Пусть даны три последовательности
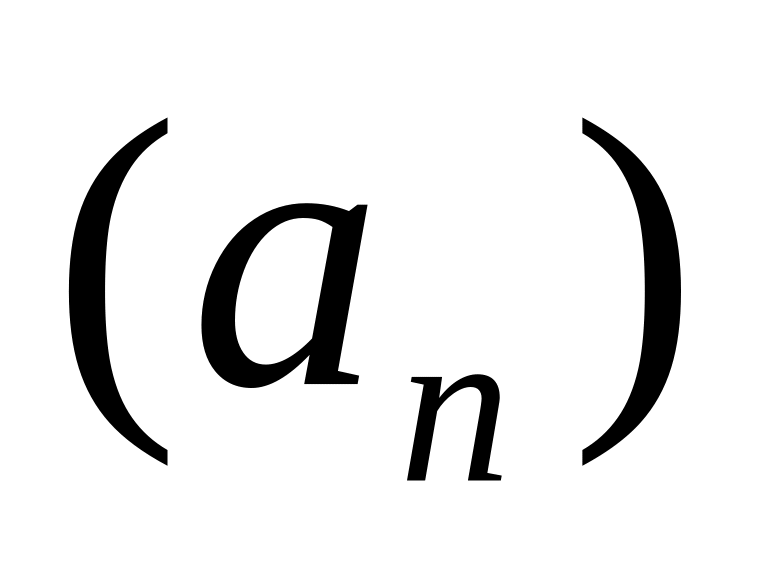 ,
,
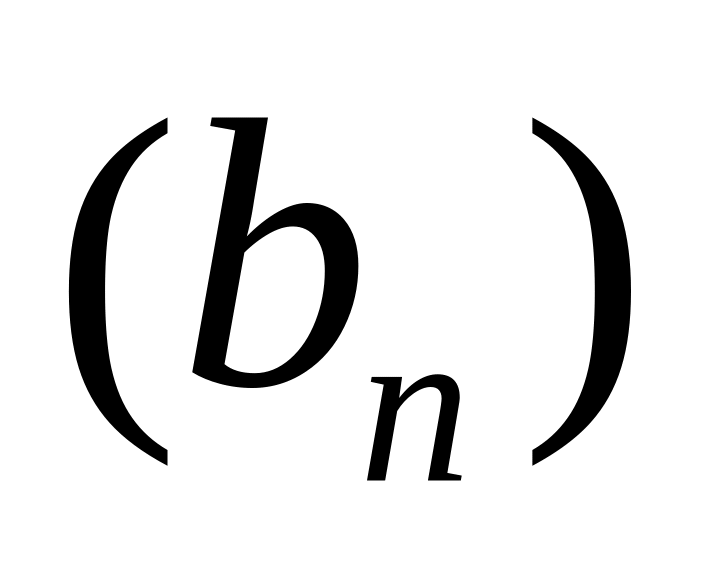 и
и
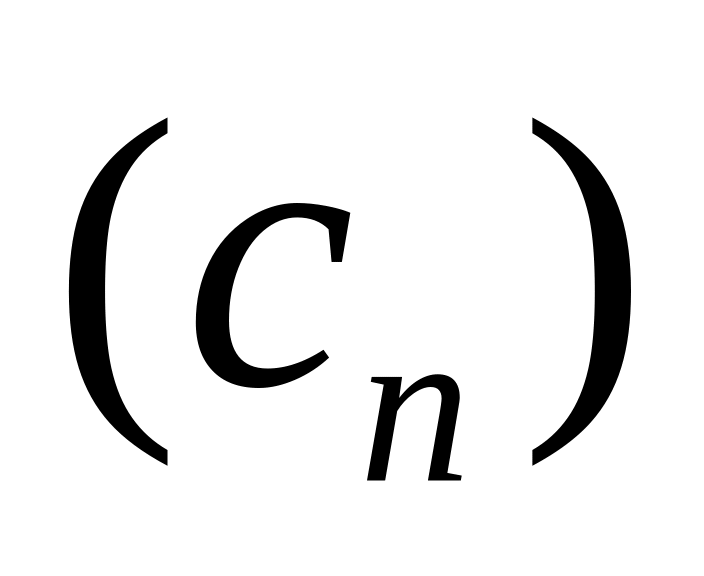 ,
причем последовательности
,
причем последовательности
 и
имеют один и тот же предел:
и
имеют один и тот же предел:
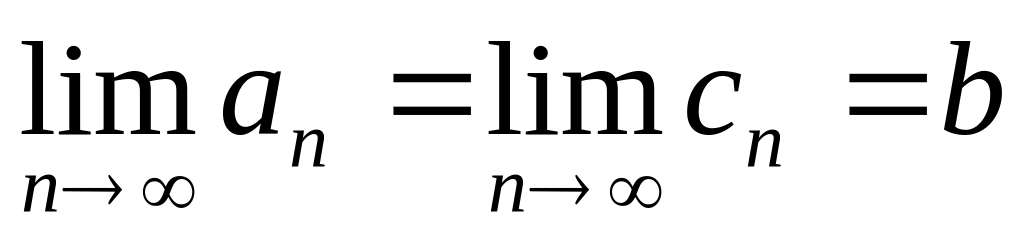 и пусть для всех натуральных
выполняется неравенство:
и пусть для всех натуральных
выполняется неравенство:
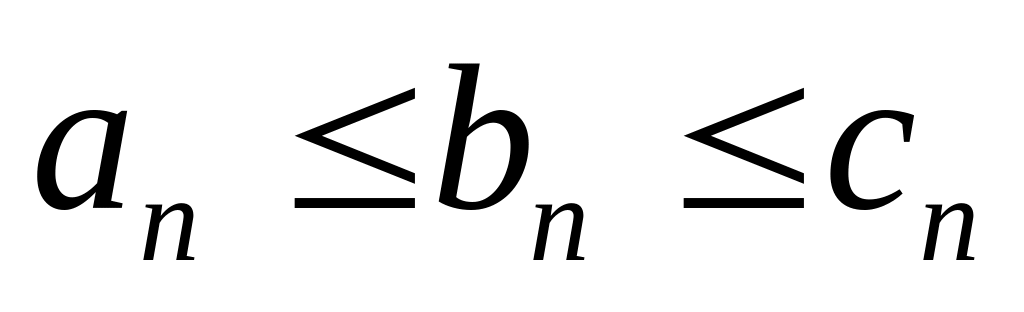 .
Тогда последовательность
сходится, причем её предел равен
.
Тогда последовательность
сходится, причем её предел равен
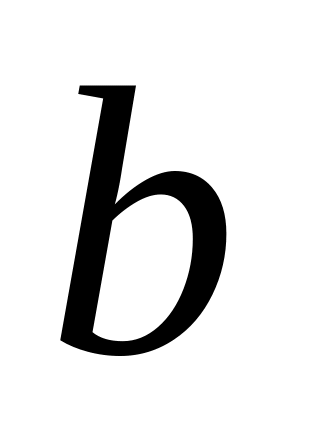 .
.
пусть
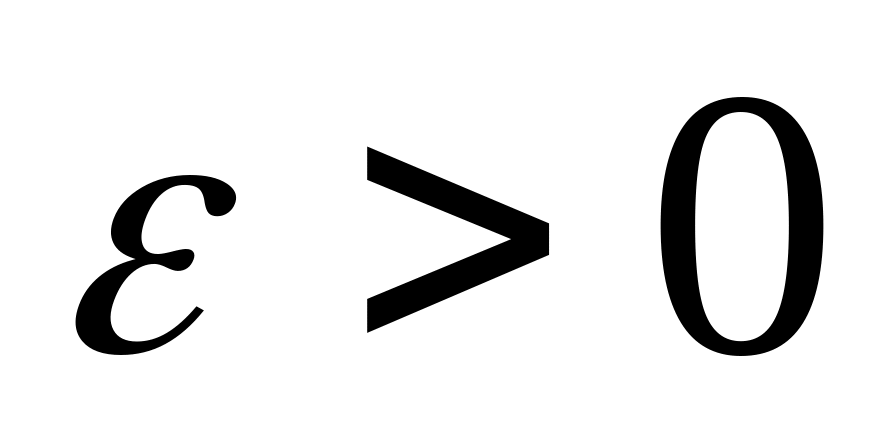 произвольное сколь угодно малое число,
тогда (
произвольное сколь угодно малое число,
тогда (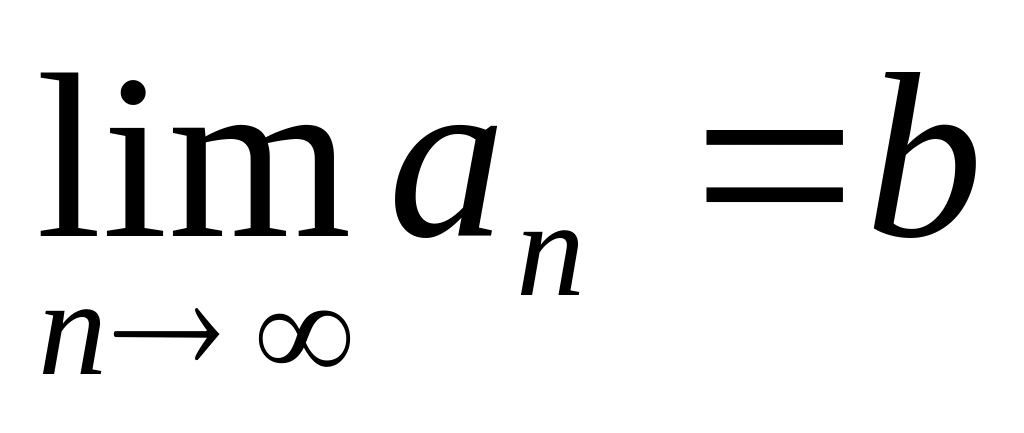 )
)

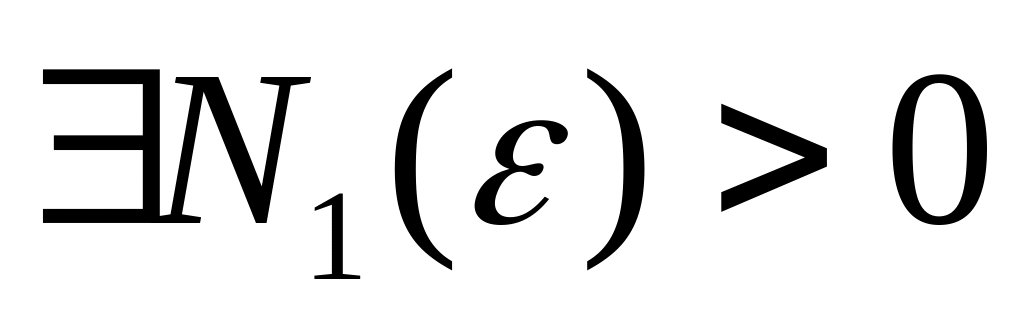
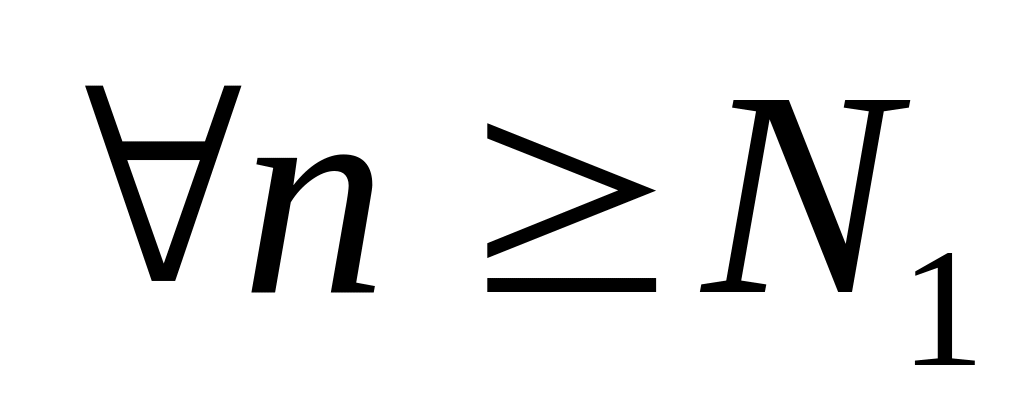
 ;
(
;
( )
)
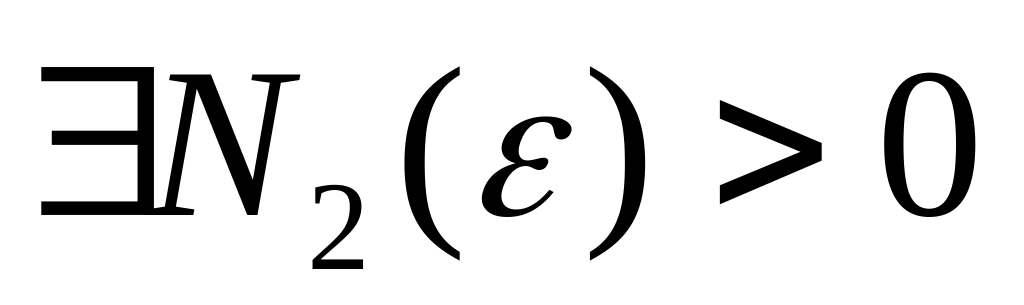
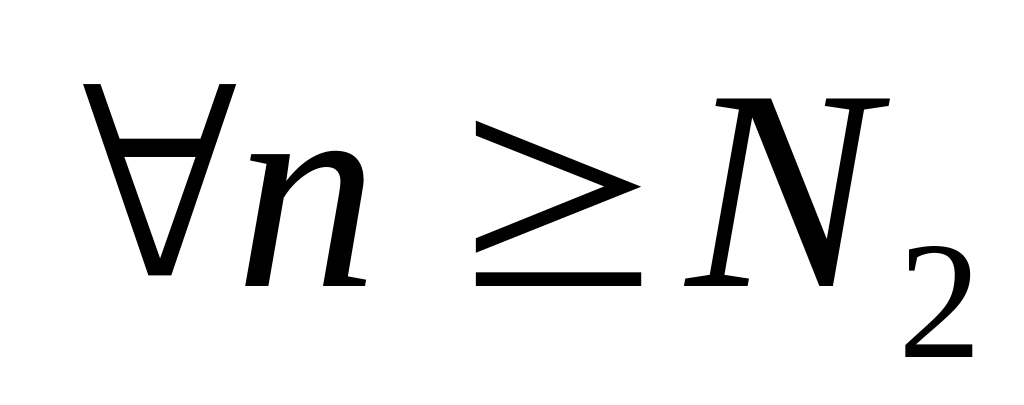
 ;
пусть
;
пусть
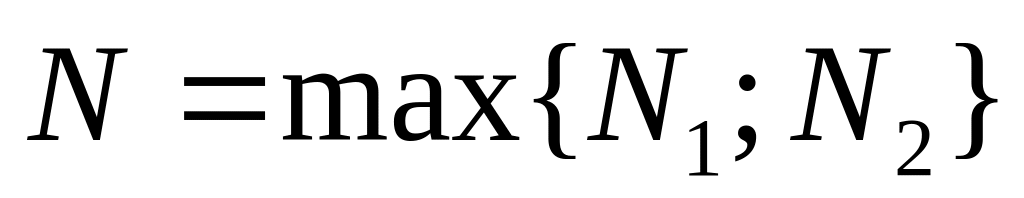 ,
тогда
,
тогда
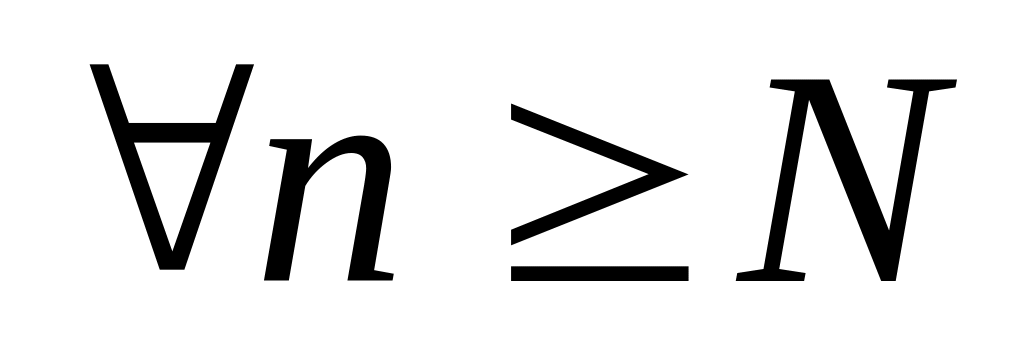 выполняются неравенства:
выполняются неравенства:
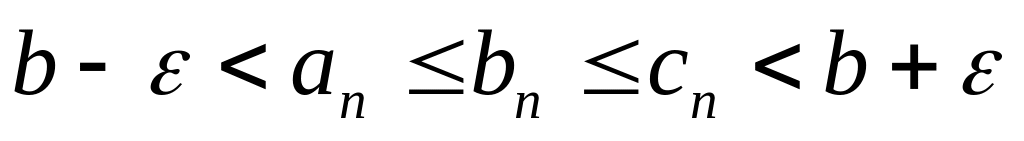 или
или
 .
.
Итак,
![]()
![]() ,
значит,
,
значит,
![]() .
.
Найти
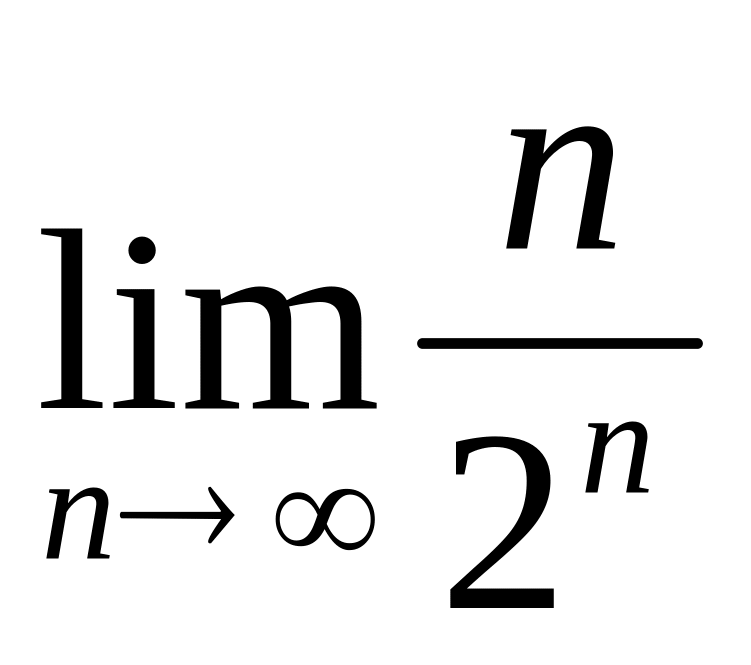 .
.
Решение:
применить теорему о пределе частного
нельзя, так как не существует предела
ни числителя, ни знаменателя. Воспользуемся
теоремой «о двух милиционерах»,
предварительно доказав неравенство:
![]() (*) для всех
(*) для всех
![]() .
.
Действительно,
при
![]() неравенство (*) выполнено:
неравенство (*) выполнено:
![]() ;
пусть при
;
пусть при
![]() ,
где
,
где
![]() ,
верно неравенство
,
верно неравенство
![]() ;
докажем, что верным будет и неравенство
;
докажем, что верным будет и неравенство
![]() .
Тогда, на основании принципа математической
индукции, неравенство (*) будет верно
для всех
.
.
Тогда, на основании принципа математической
индукции, неравенство (*) будет верно
для всех
.
Рассмотрим
![]() ,
так как
,
так как
![]() при
.
Итак,
при
.
Итак,
![]()
![]() верно
верно
![]() ,
значит,
,
значит,
![]() и
для всех
.
и
для всех
.
Известно, что
![]() и
и
![]() ,
значит,
,
значит,
![]() (по теореме «о двух милиционерах»).
(по теореме «о двух милиционерах»).
Если последовательности
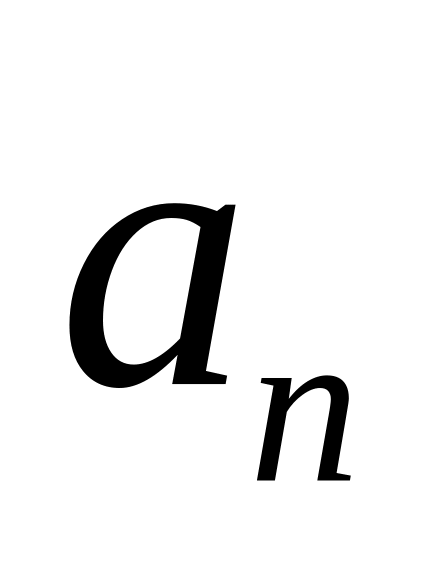 и
и
 сходятся, то:
сходятся, то:
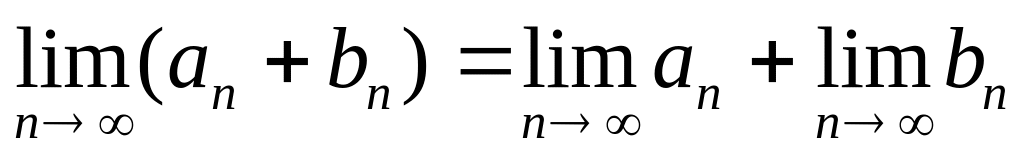 ,
,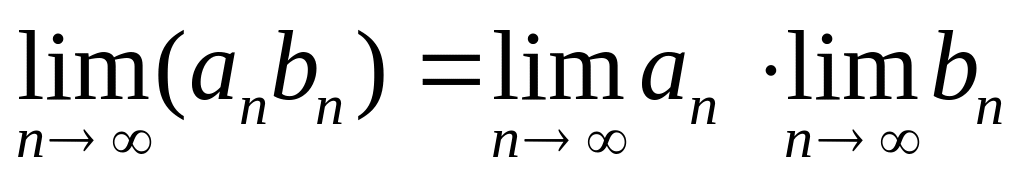 ,
,Если, кроме того,
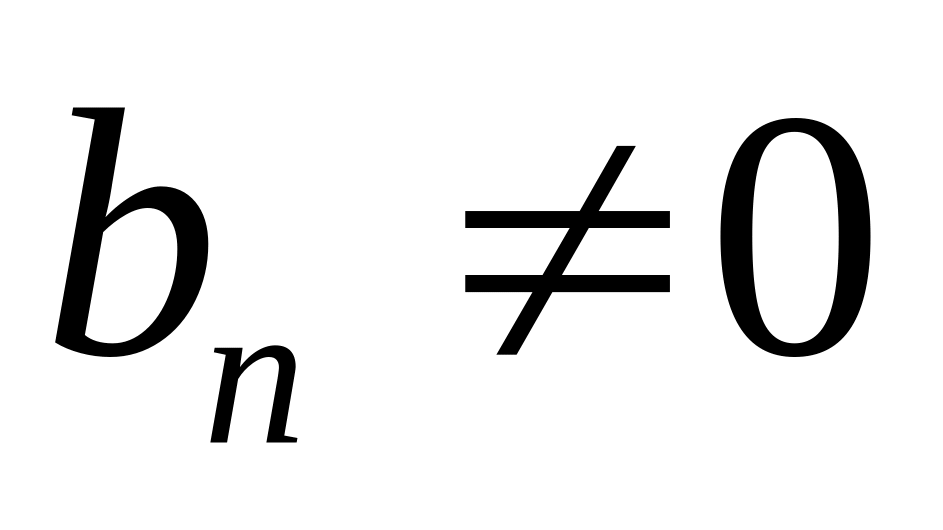 для любого
и
для любого
и
 ,
то
,
то
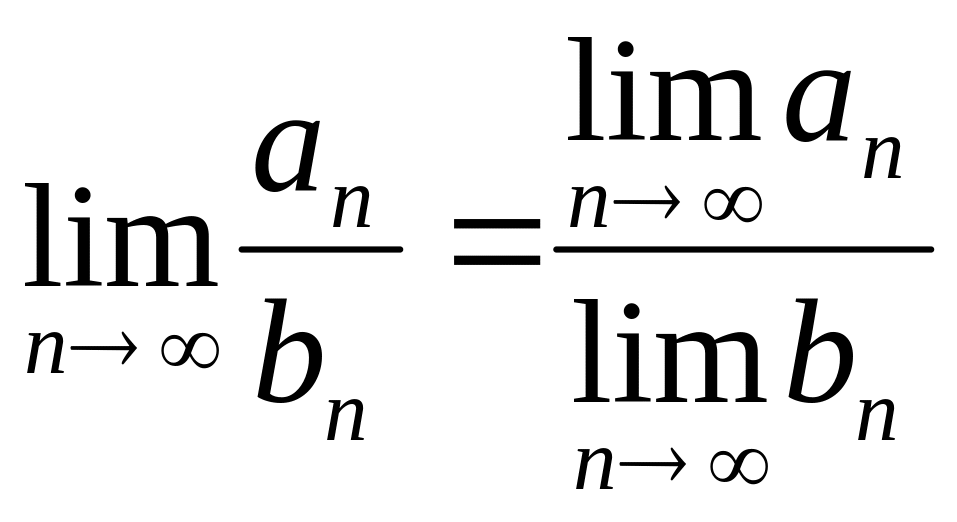 .
.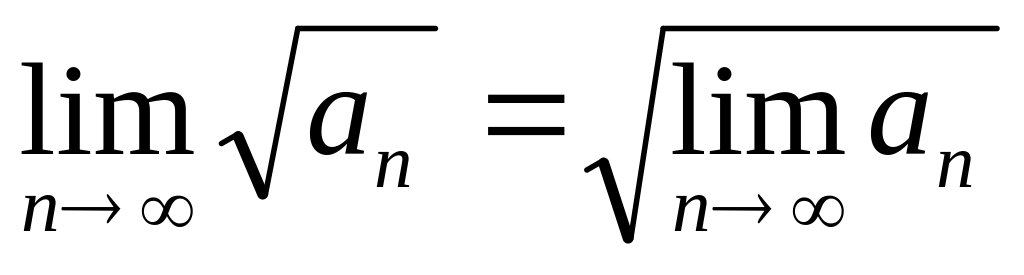 .
.
докажем часть (1) ►Теорема 4.:
Нам нужно
проверить, что
![]() ,
где
,
где
![]() ,
,
![]() .
.
Так как
![]() ,
то
,
то
![]() .
.
Так как
![]() ,
то
,
то
![]() .
.
Пусть
![]() ,
тогда
,
тогда
![]()
![]()
![]() ,
а это означает, что
,
а это означает, что
![]() ,
где
,
.
,
где
,
.
Докажем часть (2) ►Теорема 4.:
Рассмотрим
![]() ,
последовательность
имеет предел, значит, она ограничена,
то есть
,
последовательность
имеет предел, значит, она ограничена,
то есть
![]() .
.
Так как
![]() ,
то
,
то
![]() .
.
Так как
,
то
![]() .
.
Возьмем
![]() ,
тогда при
имеем
,
тогда при
имеем
![]() .
.
Итак,
![]() ,
то есть
,
то есть
![]() .
.
Части (3) и (4) доказываются аналогично.
14.Аксиома Больцано-Вейерштрасса и теорема о стягивающейся системе отрезков
В теории пределов очень важно одно свойство действительных чисел, которое обычно принимают за аксиому.
Аксиома Больцано-Вейерштрасса: всякая монотонная ограниченная последовательность имеет предел.
Данная аксиома обеспечивает только существование предела и ничего не говорит о его величине. Однако иногда достаточно знать это, чтобы его найти.
Рассмотрим пример:
Дана последовательность
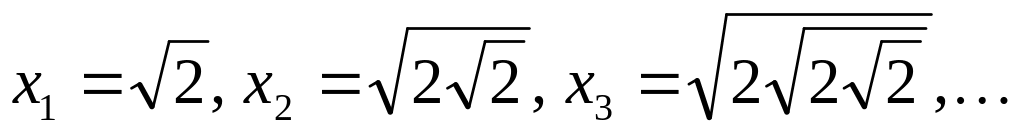 .
Докажем, что она сходится и найдем ее
предел.
.
Докажем, что она сходится и найдем ее
предел.
Для этой
последовательности справедливо равенство
![]() .
(*)
.
(*)
Для доказательства
существования предела применим аксиому
Больцано-Вейерштрасса. По индукции
можно доказать, что
![]() .
Поэтому последовательность
.
Поэтому последовательность
![]() монотонна и ограничена.
монотонна и ограничена.
Если
последовательность
![]() имеет предел
имеет предел
![]() ,
то левая часть равенства (*) стремится
к
,
то левая часть равенства (*) стремится
к
![]() ,
а правая - к
,
а правая - к
![]() .
Получаем
.
Получаем
![]() ,
,
![]() или
или
![]() .
Очевидно,
не является пределом последовательности
.
Значит,
.
Очевидно,
не является пределом последовательности
.
Значит,
![]() .
.
Аналогично можно
доказать, что
![]() ,
если
,
если
![]() .
.
Пусть даны две последовательности
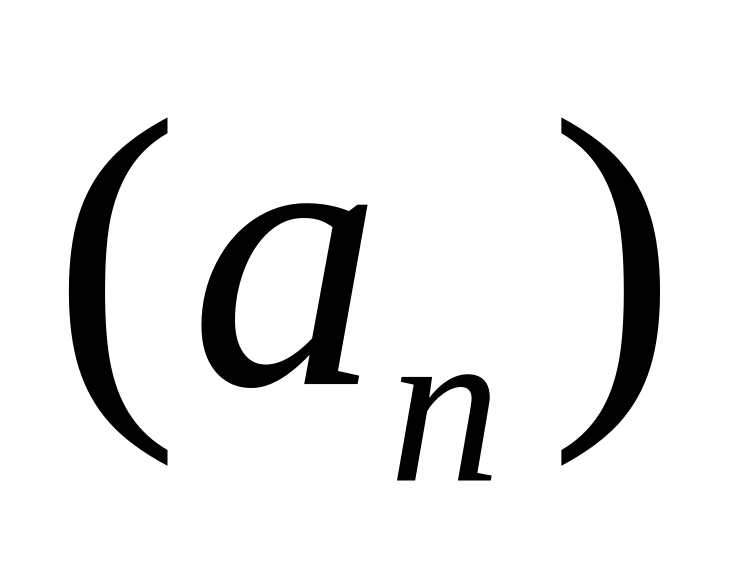 и
и
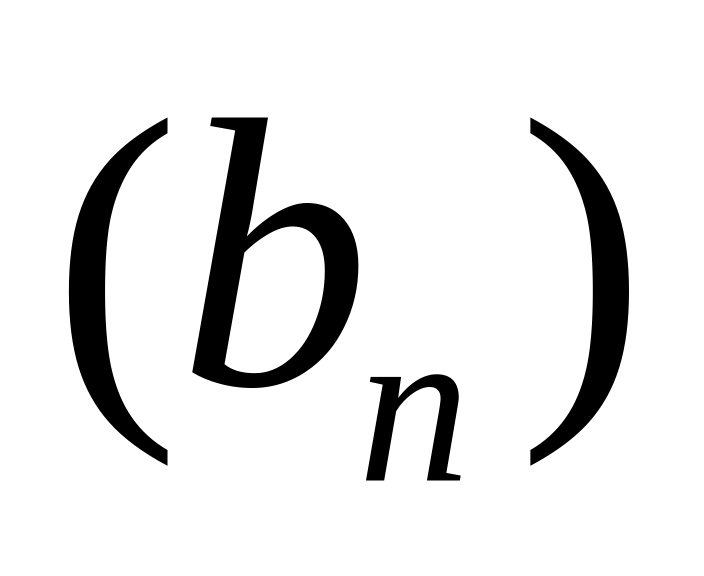 такие, что:
такие, что:
последовательность монотонно не убывает:
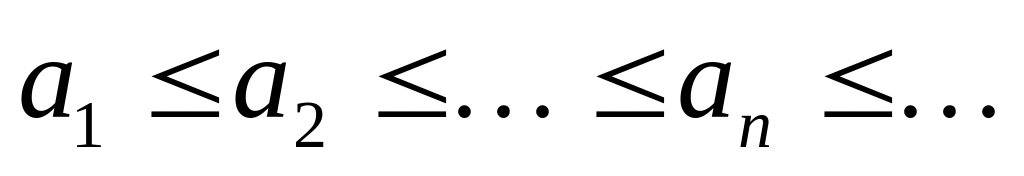 ;
;последовательность монотонно не возрастает
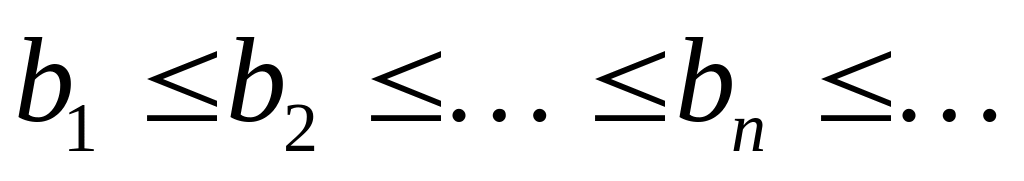 ;
;для любого выполняется неравенство
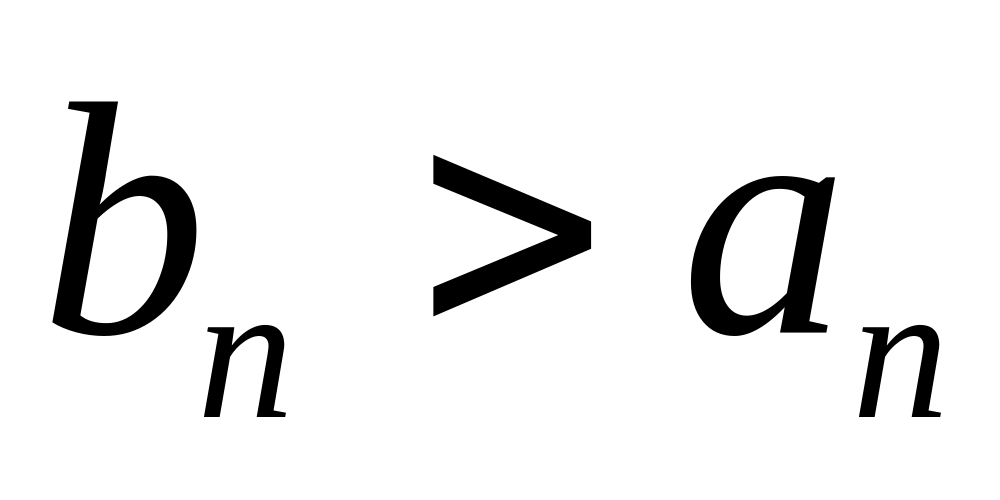 ;
;разность
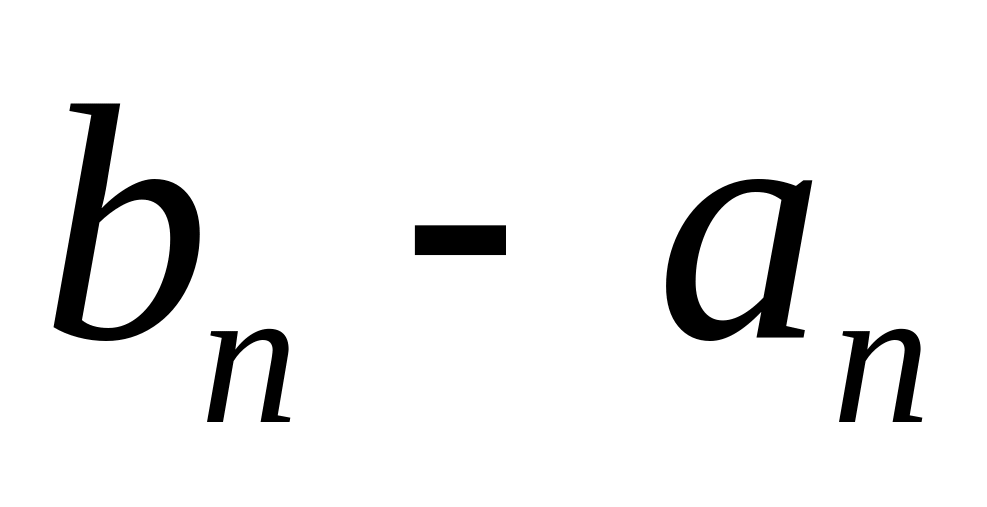 стремится к нулю при
стремится к нулю при
 ,
,
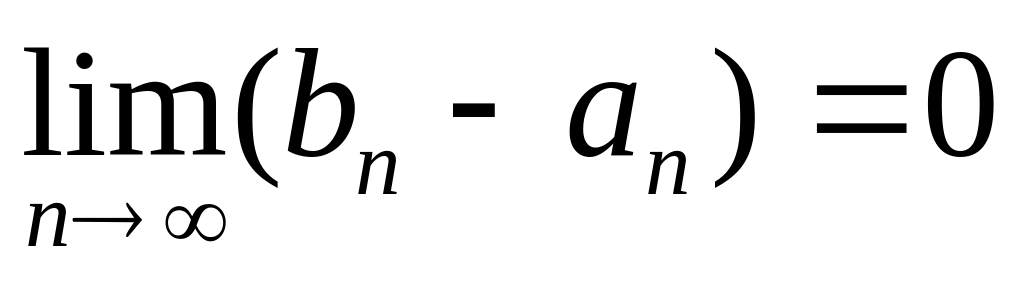 .
.
Тогда существует
число
![]() ,
являющееся общим пределом этих
последовательностей:
,
являющееся общим пределом этих
последовательностей:
![]() ,
причем, для всех
выполняется неравенство
,
причем, для всех
выполняется неравенство
![]() .
.
рассмотрим последовательность , она не убывает и ограничена сверху:
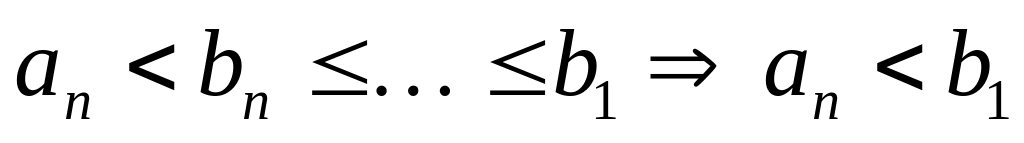 ,
значит у нее есть предел (аксиома
Больцано – Вейерштрасса), обозначим
его
,
значит у нее есть предел (аксиома
Больцано – Вейерштрасса), обозначим
его
 .
.
Аналогично, для
:
она не возрастает и ограничена снизу:
![]() ,
значит, в силу аксиомы Больцано –
Вейерштрасса, последовательность
имеет предел, обозначим его
,
значит, в силу аксиомы Больцано –
Вейерштрасса, последовательность
имеет предел, обозначим его
![]() .
.
Рассмотрим
условие 4):
![]() ;
поскольку существует предел каждого
слагаемого, можно применить теорему о
пределе суммы (разности):
;
поскольку существует предел каждого
слагаемого, можно применить теорему о
пределе суммы (разности):
![]()
![]() ,
значит,
,
значит,
![]() и последовательности имеют общий предел
и последовательности имеют общий предел
![]() .
.
Последовательности и определяются рекуррентными соотношениями
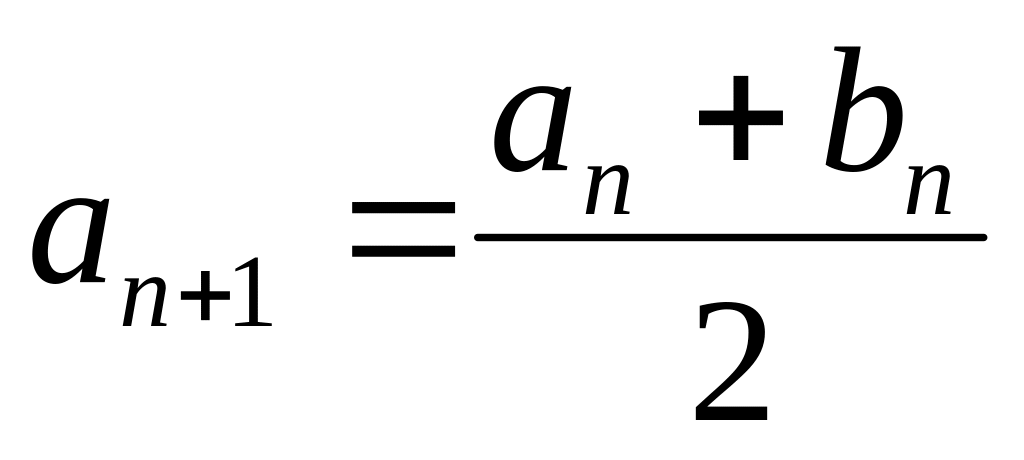 ,
,
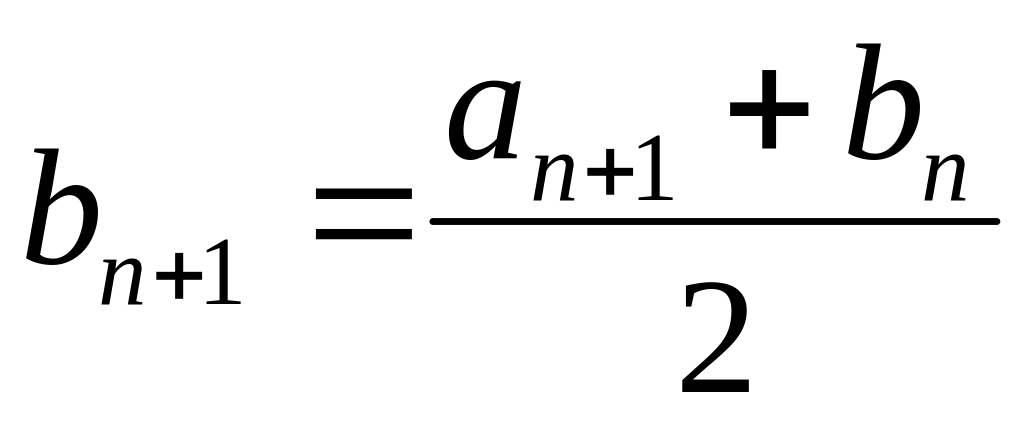 ,
причем
,
причем
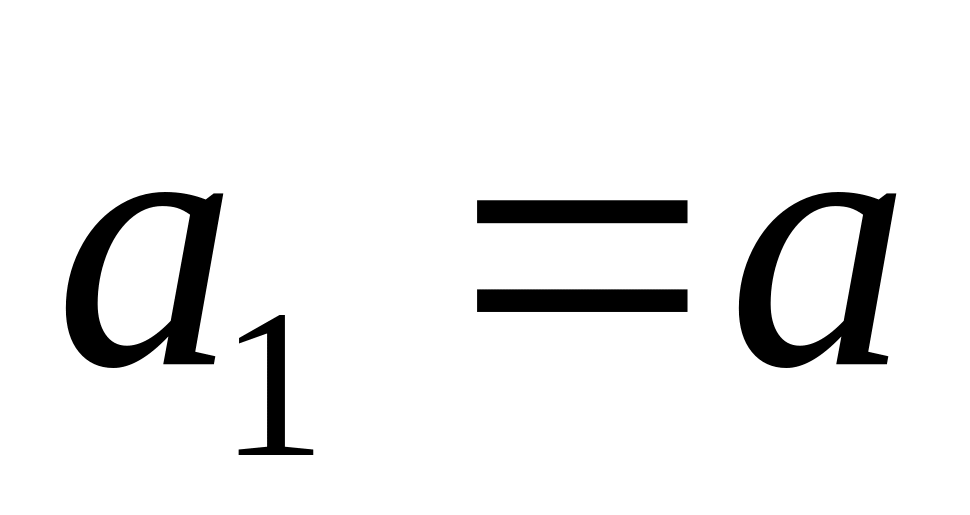 ;
;
 где
где
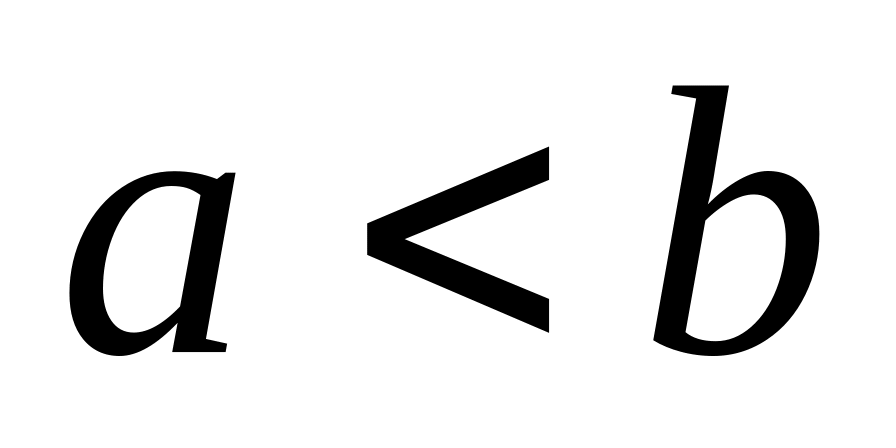 .
Докажите, что они имеют общий предел.
.
Докажите, что они имеют общий предел.
из условий следует, что
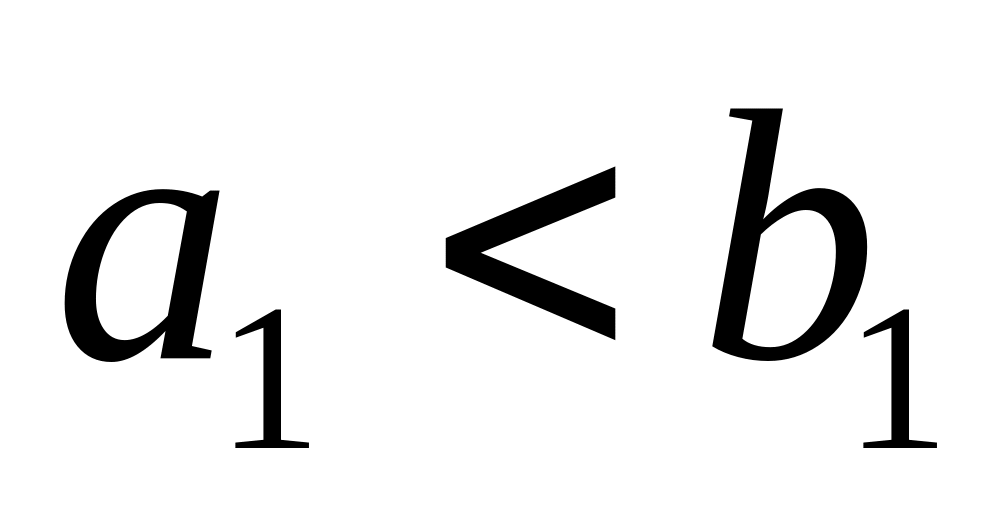 ;
докажем, что
;
докажем, что

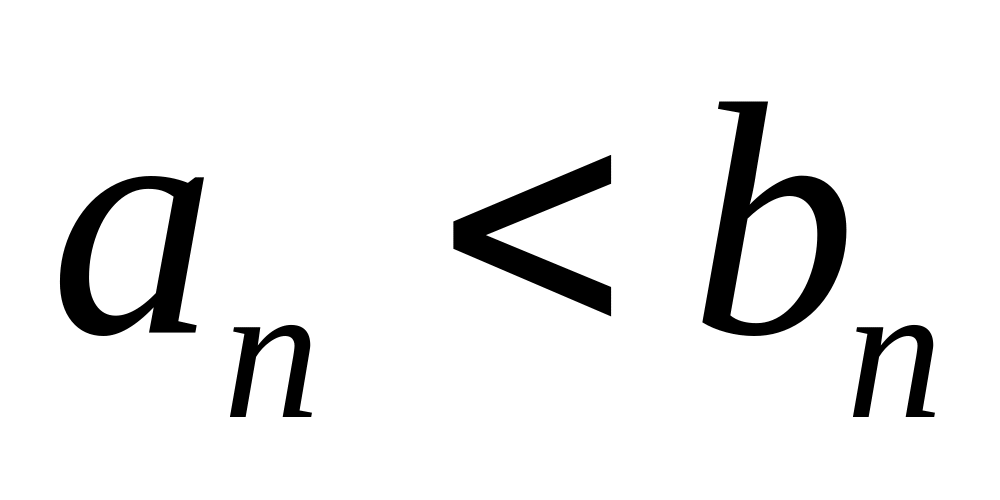 ,
используя метод математической индукции.
Пусть для
,
используя метод математической индукции.
Пусть для
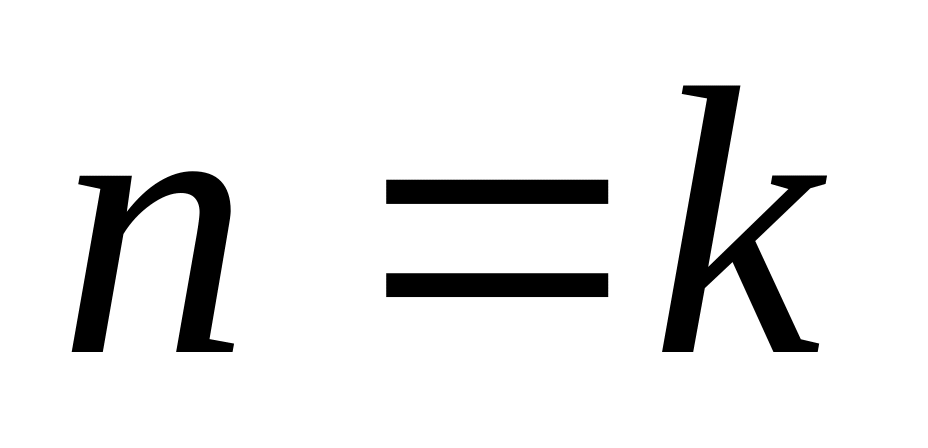 ,
где
,
где
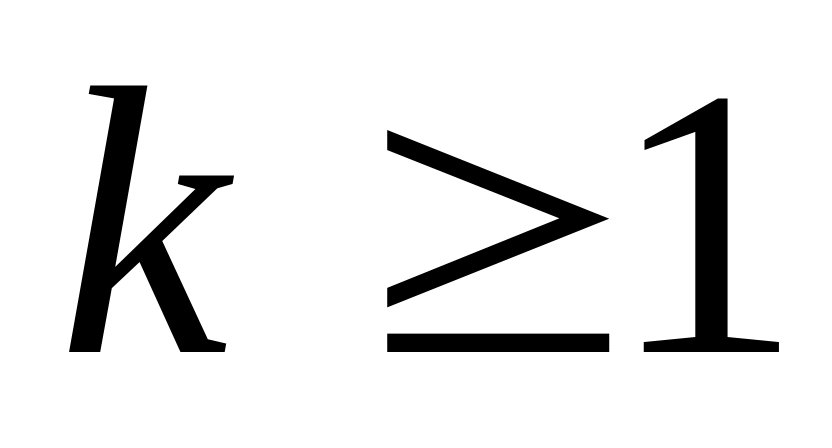
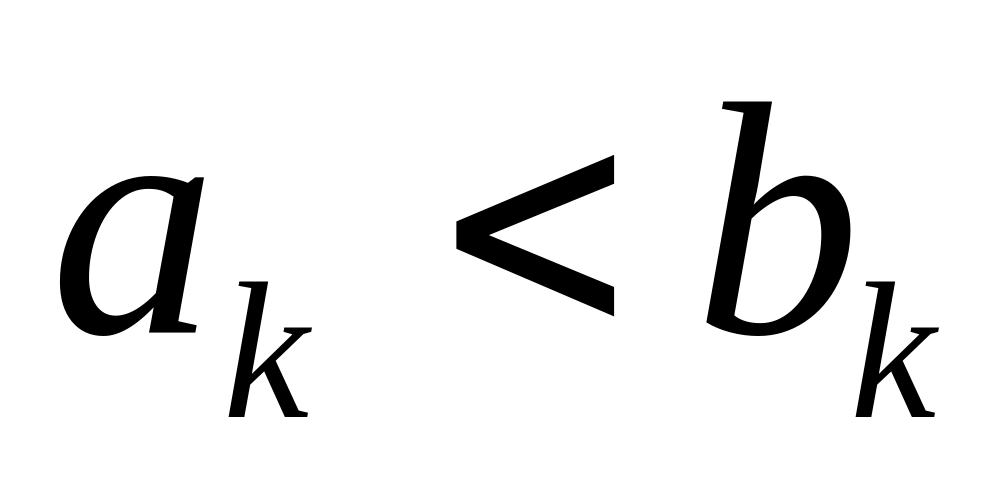 ,
тогда
,
тогда
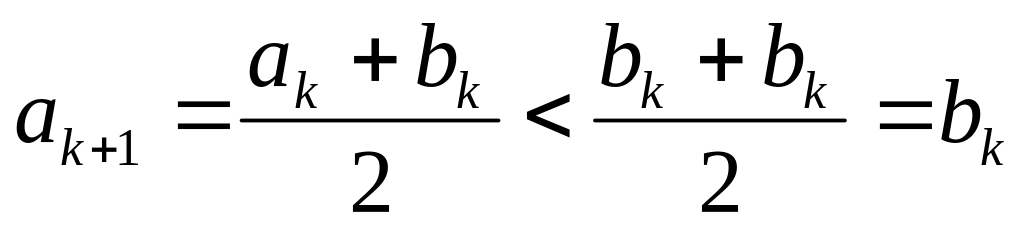 ;
значит,
;
значит,
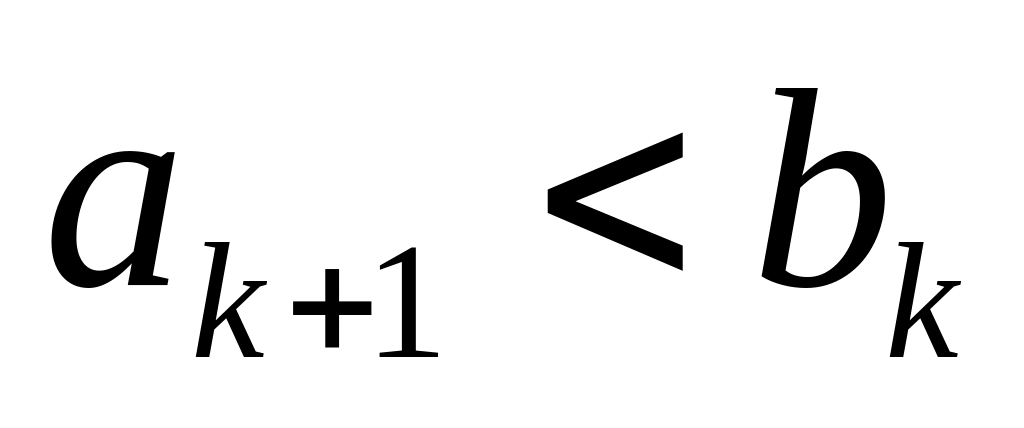 ;
;
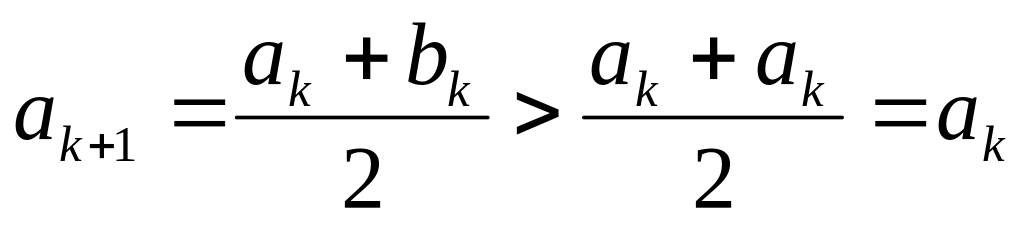 ;
значит,
;
значит,
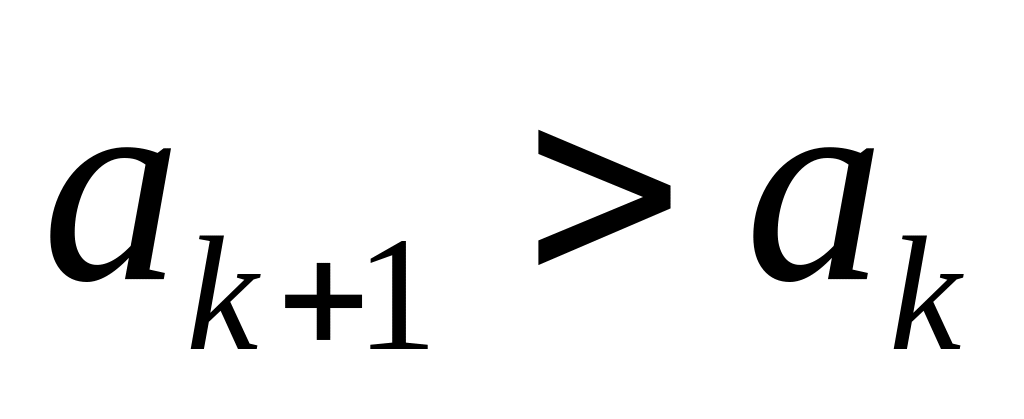 ;
;
 ;
значит,
;
значит,
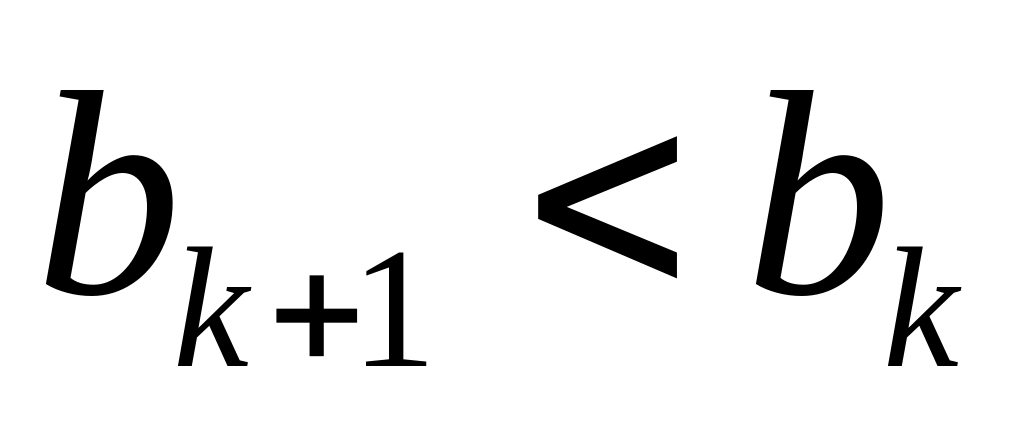 ;
;
 ;
значит,
;
значит,
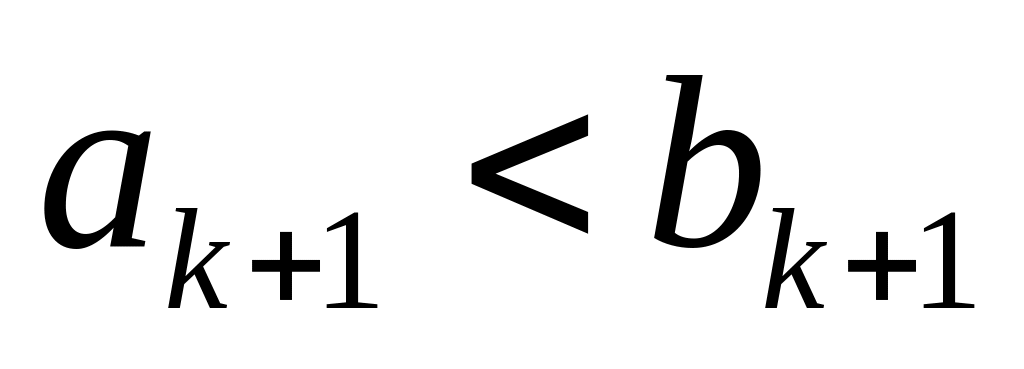 ;
отсюда следует не только тот факт, что
,
но и возрастание последовательности
,
убывание последовательности
.
;
отсюда следует не только тот факт, что
,
но и возрастание последовательности
,
убывание последовательности
.
Рассмотрим
![]() ,
поэтому
,
поэтому
![]() и
.
и
.
В силу ►Теорема 5. последовательности и имеют общий предел.
►Теорема 5. имеет
следующий геометрический смысл.
Рассмотрим отрезки
![]() .
Из условий следует, что отрезок
.
Из условий следует, что отрезок
![]() является частью отрезка
(так как
является частью отрезка
(так как
![]() и
и
![]() ),
кроме того, длины отрезков
стремятся к нулю, когда
.
Неравенство
),
кроме того, длины отрезков
стремятся к нулю, когда
.
Неравенство
![]() означает, что точка принадлежит всем
отрезкам
.
означает, что точка принадлежит всем
отрезкам
.
Таким образом, геометрическая формулировка ►Теорема 5. такова:
Пусть последовательность отрезков
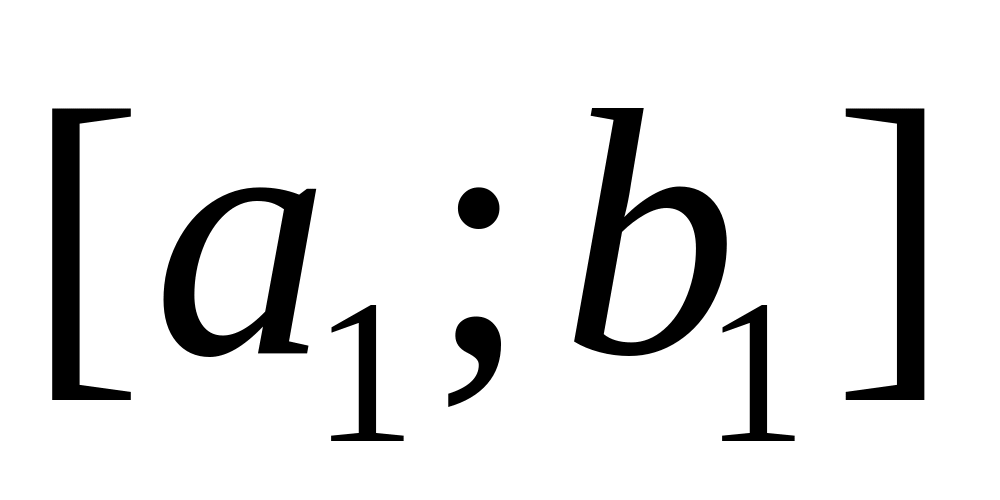 ;
;
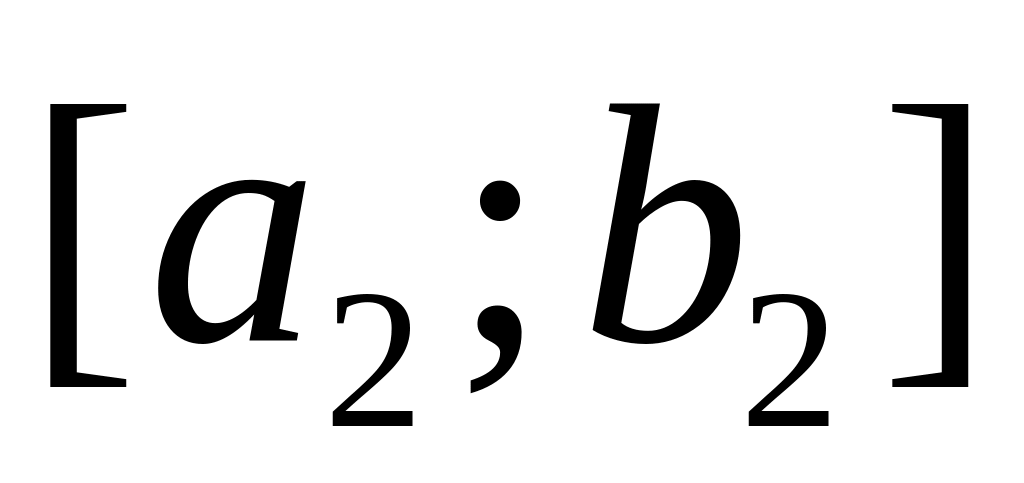 ;
…
;
… такова, что:
;
…
;
… такова, что:
каждый следующий отрезок является частью предыдущего:
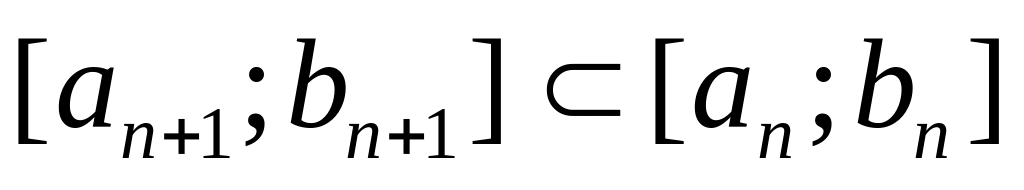 ;
;длины отрезков стремятся к нулю при , .
Тогда существует единственная точка , принадлежащая всем этим отрезкам, причем .
Говорят, что система отрезков стягивается в точку , поэтому ►Теорема 6. называют теоремой о стягивающейся системе отрезков. Эта теорема играет существенную роль в теории действительных чисел.
