Глава 2.Числовые последовательности и их свойства §3.Числовые последовательности

12.Основные определения

Выпишем в порядке возрастания положительные числа, кратные :

Каждому натуральному числу ставится в соответствие определенное число ; таким образом, имеем функцию, определенную на множестве натуральных чисел .

18. Функцию¹, определенную на множестве натуральных чисел называют числовой последовательностью.

19. Числа, образующие последовательность, называются членами последовательности. Обозначается последовательность: 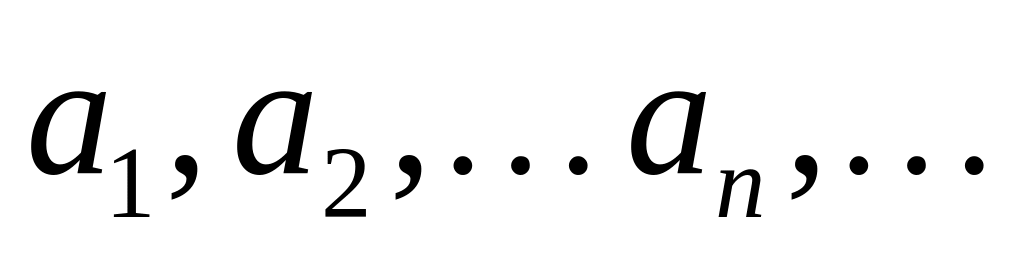или .

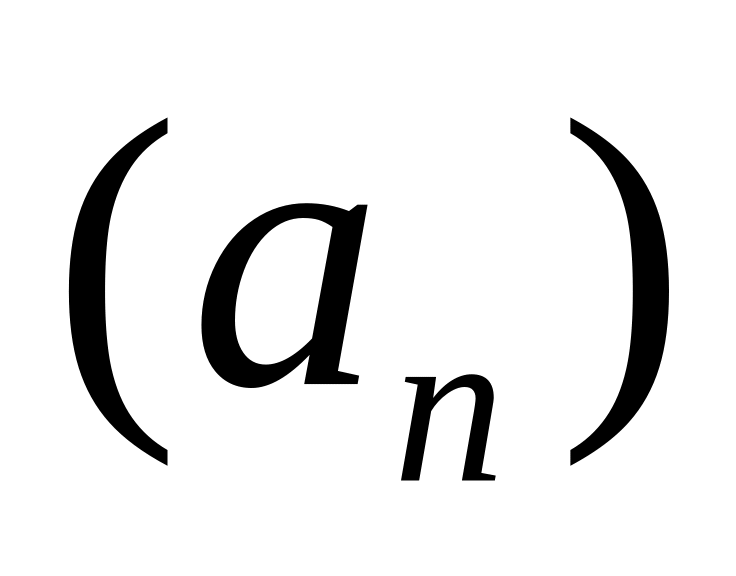20. Последовательность, имеющая конечное число членов, называется конечной.

13.Способы задания последовательностей

Последовательности задаются несколькими способами: аналитическим (формульным), словесным, графическим.

Аналитический способ: указывается формула, связывающая значение -ого члена последовательности с его номером . Зная ее, мы можем получить любой член последовательности.

25. 

26. 

27. 

18. Последовательность, общий член которой не зависит от , называется постоянной (см. Пример 27.).

Используется также рекуррентный способ: задаются несколько первых членов последовательности и формула, называемая рекуррентным соотношением, выражающая следующие члены последовательности через предыдущие, например: при (это последовательность Фибоначчи).

Словесный способ: закон соответствия между номером члена и значением этого члена может быть задан словесно.

25. Каждому натуральному числу сопоставляется число, равное -ому десятичному знаку после запятой числа в десятичной записи. Этот закон определяет последовательность, у которой ;…

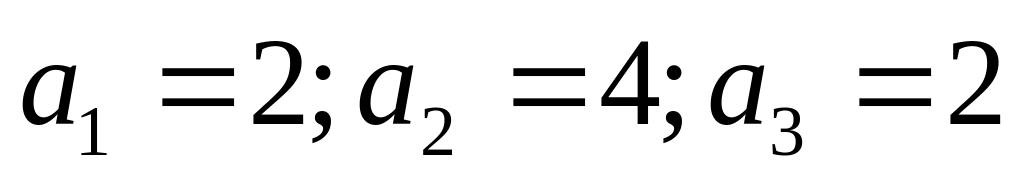26. Последовательность всех простых чисел 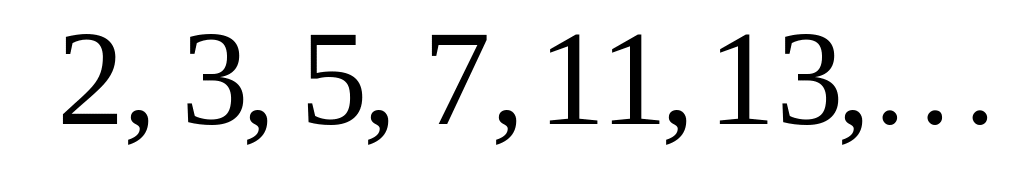Мы можем найти любой член этой последовательности, однако нет формулы для -го простого числа, и нет формулы, выражающей -ое простое число через предыдущие.

Графический способ: используются две интерпретации - двумерная (на плоскости) и одномерная (на числовой прямой).

Т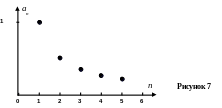 ак как последовательность является функцией, то геометрически эту функцию можно изобразить с помощью ее графика, то есть множества точек координатной плоскости. Например, .

Ч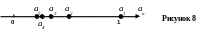 лены последовательности изображаются также точками координатной прямой. Например, .

Примечание: по известным первым членам последовательности, если нет никаких других указаний, невозможно указать закон ее образования. Так, четыре первые члена некоторой последовательности: могут быть, например, началом последовательности нечетных чисел или последовательности с формулой общего члена .

Для каждой последовательности должен быть задан закон, по которому мы можем получить любой ее член. В каком виде задан этот закон – не имеет значения.

14.Монотонность числовых последовательностей

18. Последовательность называется возрастающей, если для любого .

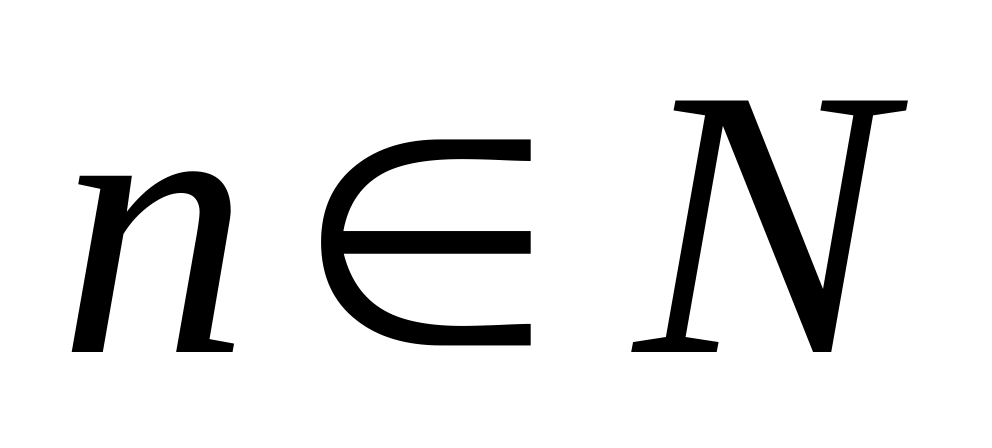
19. Последовательность называется убывающей, если для любого .

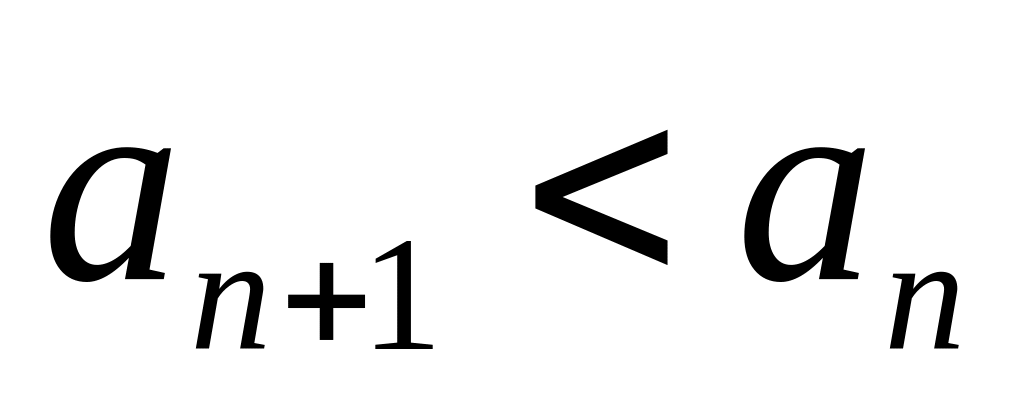Последовательность – возрастающая, так как , значит, , последовательность – убывающая, так как , то есть .

18. Последовательность называется неубывающей, если 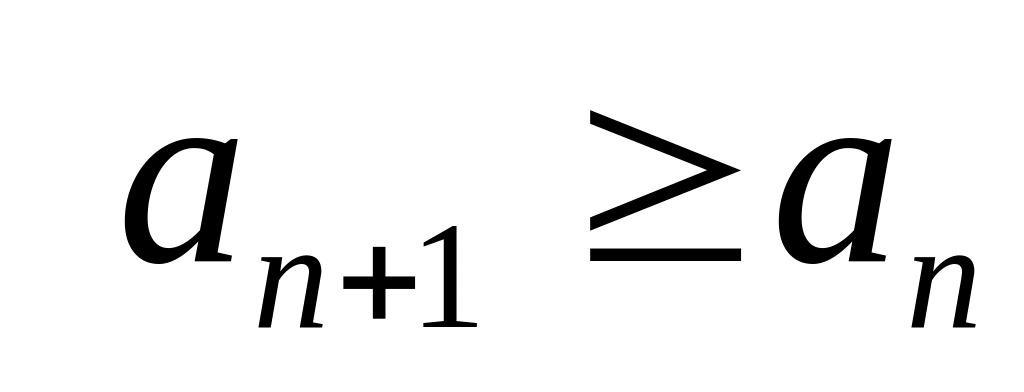для любого .

19. Последовательность называется невозрастающей, если 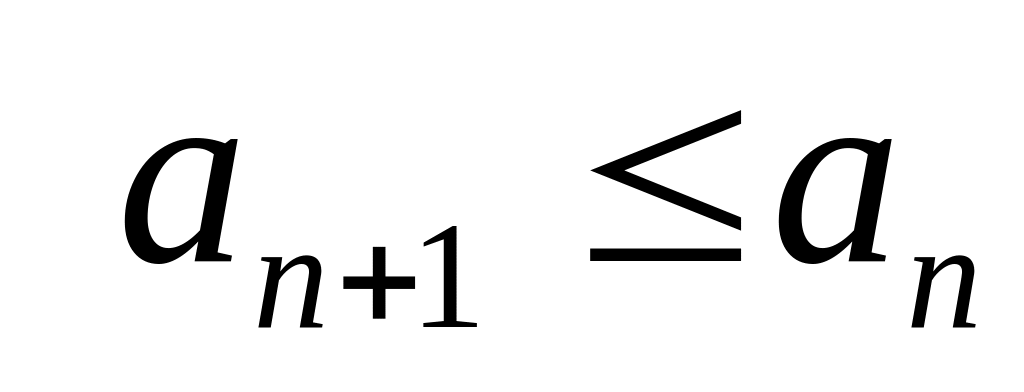для любого .

20. Возрастающие, убывающие, невозрастающие и неубывающие последовательности называются монотонными.

25. Докажите, что последовательность монотонна.

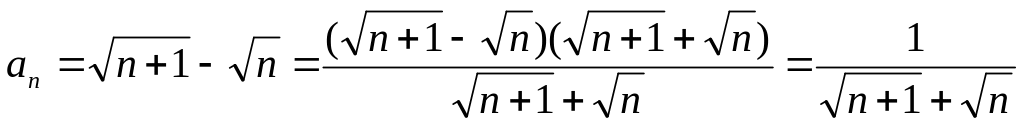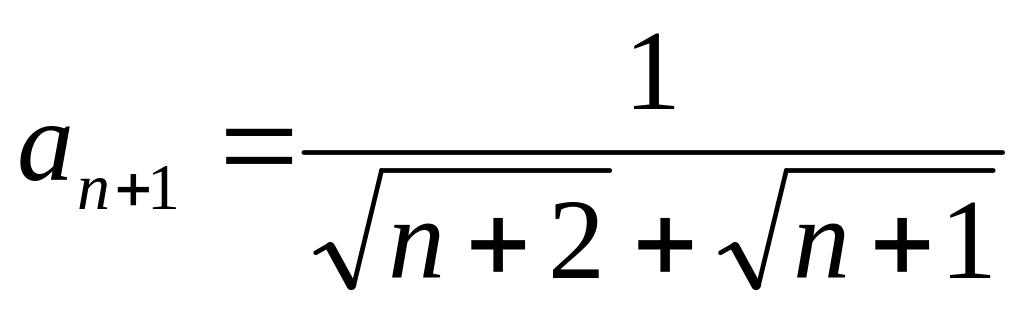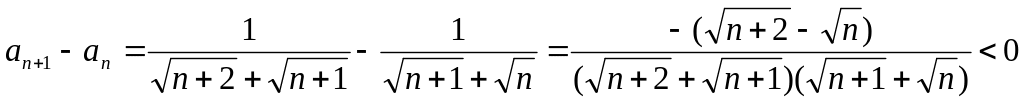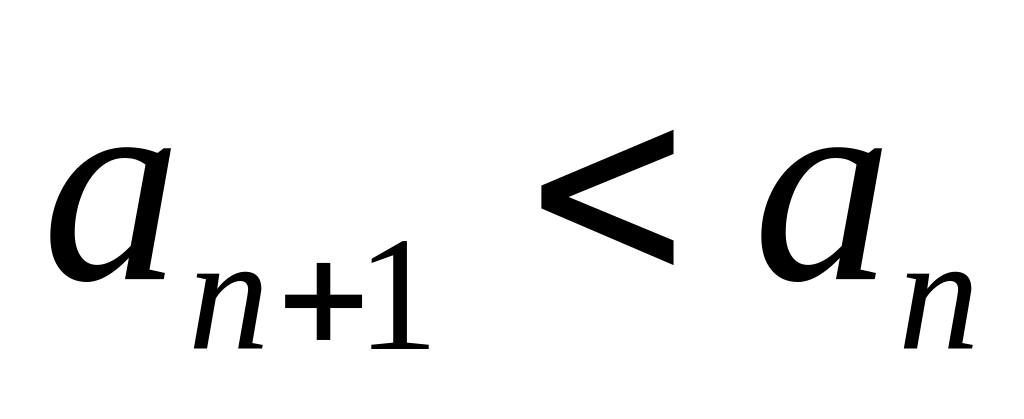1. , аналогично ; , следовательно, , то есть последовательность убывающая.