IX.2. Критерії перевірки гіпотез.

    9.2.1. Критерій  .     Критерій   був запропонований Пірсоном в 1903Р., хоча повністю цей метод був запропонований Фішером, який опублікував в 1924р. відповідні таблиці критичних величин, які використовуються в даний час. Статистика   визначається наступним виразом: 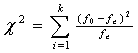       , де     f₀ – частота, яка спостерігається для кожної групи або інтервалу;     f_e – очікувана частота для кожної групи або інтервалу.     Сума по k - це передбачена теоретичним розподілом сума по всіх групах або інтервалах.     Якщо   = 0, то спостерігаємі і теоретично передбачені значення частот точно співпадають.      Якщо   > 0, то повного співпадіння немає. Чим більше  , тим більше розходження між спостерігаємими і очікуваними значеннями. Для того щоб оцінити наскільки спостерігаємі дані визначаються тільки випадковими величинами, слід порівнювати розрахункові значення з табличними значеннями  . Значення статистики   табульовані для різних степенів вільності і різних рівнів довірчої ймовірності 1-  , де   - рівень значимості. При практичному використанні цієї статистики висувається так звана нульова гіпотеза Н₀про те, що між спостерігаємим і очікуваним розподілом з тими самими параметрами немає значних відхилень. Якщо при перевірці цієї гіпотези розрахункова величина   виявляється більшою критичного табличного значення для даного рівня довірчої ймовірності і відповідного числа степенів вільності, то можна заключити, що при даному рівні довірчої ймовірності спостерігаємі частоти значно відрізняються від очікуємих, і тоді слід було б відкинути гіпотезу H₀.      При застосуванні метода перевірки гіпотез по критерію   слід пам'ятати наступне:

1. відносні значення частот або їх значення, які вираженні в %, брати не можна. Повинні використовуватися дані прямих спостережень або абсолютні значення частот ;

2. значення спостерігаємих частот для кожної групи або інтервала повинні бути не менше 5 ;

3. число степеней вільності задається виразом ν=k-1-m , де k - кількість груп або інтервалів ; m - число параметрів, які визначаються дослідним шляхом або на основі вибіркових даних для обчислювання очікуваних значень частот.

    Розглянемо приклад.     Перевіряються дані таблиці для дискретної величини на відповідність розподілу Пуасона при довірчій ймовірності 0.95       , де P_x(n) – ймовірність наступлення n подій; е=2.71828; λ – додатня частота, яка одночасно є середнім значенням і дисперсією.      Було підраховано, що λ = 0.5577, тому гіпотеза H₀ формулюється наступним чином: не має суттєвих відмінностей між спостерігаємими даними і даними, які отримуються із закону Пуасона з математичним очікуванням або середнім λ = 0.5577. Підставивши значення λ і послідовність n=0,1,2,... отримаємо наступні результати:

    Для отримання f_e множимо відповідну величину P(n) на 509. Розрахункова величина   = 5.10. Для довірчої ймовірності 0.95 і числа ступеней вільності ν=4-1-1=2 знаходиться   = 5.99. Таким чином, оскільки розрахункова величина   < табличного критичного значення  , ми не відкидаємо гіпотезу H₀. Останні 3 групи значень були об'єднані з тим, щоб отримати значення частоти принаймні = 5 в кожній групі. Таким чином, замість вихідних 6 груп отримано 4. При визначенні числа ступеней вільності значення зменшено на 1, бо для розрахунку очікуваних частот використовується величина λ, яка отримана з даних спостережень.     9.2.2. Критерій Колмогорова-Смірнова.     Цей критерій запропонований Смірновим в 1939р. і в подальшому розвинутий самим автором і Колмогоровим. Він застосовується тоді, коли перевіряємий розподіл неперервний і відомі середнє і дисперсія сукупності. Таблиця його критичних значень була опублікована Смірновим в 1948р. Подібно критерію   критерій Колмогорова-Смірнова може бути використаний для перевірки відповідності між розподілом сукупності емпіричних даних і деяким теоретичним розподілом. Перевірка здійснюється шляхом задання інтегральної функції, яка випливає з теоретичного розподілу, і її порівняння з інтегральною функцією розподілу емпіричних даних.     Порівняння базується на вибірковій групі, в якій експериментальний розподіл має найбільше абсолютне значення по відношенню теоретичного. Далі ця абсолютна різниця співставляється з критичним значенням з метою визначення чи може таке відхилення бути випадковим при заданому законі розподілу.     Приклад.     Візьмемо дані попередньої таблиці, які перевіряються по критерію   на відповідність розподілу Пуасона. Для цієї сукупності λ = 0.5577. Гіпотеза H₀ полягає в тому, що немає суттєвих розходжень між спостерігаємими даними і тими, які повинні отримуватися у випадку розподілу Пуасона із середнім значенням 0.5577 і n=509.     Перш за все, необхідно знайти два інтегральних розподіли – із спостерігаємих даних і із теоретичного розподілу – і знайти абсолютні різниці для всіх груп значень випадкових величин. Це зроблено в наступній таблиці 

число запитів	I спостерігаєма частота	II спостерігаєма ймовірн.	III теоретична ймов.	IV інтегральна ймов.II	V інтегральна ймов. III	VI абсолютна різниця IV-V
0	315	0,619	0,571	0,619	0,571	0,048
1	142	0,279	0,319	0,898	0,890	0,008
2	40	0,078	0,089	0,976	0,979	0,003
3	9	0,018	0,017	0,994	0,996	0,002
4	2	0,004	0,003	0,998	0,999	0,001
5	1	0,002	0,001	1,000	1,000	0,000

    Найбільша абсолютна різниця 0.048 отримується в групі, яка відповідає нульовому числу запитів. Це значення порівнюється з критичним значенням, яке знаходиться по таблиці при n=509 і  =0.05, D_кр= =0.0603 для n>=30. Оскільки 0.048 менше критичного значення, то гіпотеза H₀ про відповідність розподілу закону Пуасона приймається. Для деяких таблиць критичних значень розраховані статистики: 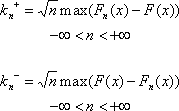         F(x) - теоретична функція розподілу ;     F_n(x) - емпірична функція розподілу ;     F_n(x)=(кількість значень х₁, х₂,...,х_n<=x)/n, де     n - довжина вибірки.     Статистики k_n⁺ і k_n^- можна визначити за допомогою наступного алгоритму:

1. визначаються вибіркові значення x₁, x₂,...., x_n;

2. значення x_i розміщується в порядку зростання, так щоб x₁<=x₂<=x₃<=...<=x_n ;

3. необхідні статистики обчислюються за формулами:

    

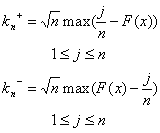
    Виникає питання, коли слід користуватися критерієм  , а коли критерієм Колмогорова-Смірнова. При відносно малих об'ємах вибірки критерій   взагалі непридатний і слід користуватися критерієм Колмогорова-Смірнова. До того ж, коли об'єм вибірки настільки малий, що для використання критерію   слід об'єднувати сусідні групи, потужність цього критерію в якійсь степені понижується. Однак, якщо об'єм вибірки достатньо великий, переважним є критерій  . Критерій   досить потужний для вибірок n>=100. Критерій Колмогорова-Смірнова - для 10<=n<=99. При використанні як критерію  , так і критерію Колмогорова-Смірнова є можливість задавати число груп або інтервалів вибірки. Правильний вибір цього числа має велике значення, оскільки визначає число степенів вільності при використанні критерію. Чим більше це число, тим надійніше критерій розпізнає характер розподілу. У випадку критерію   число груп часто визначається з умови, щоб у кожну групу попало не менше 5 експериментальних точок. У випадку використання критерію Колмогорова-Смірнова дані можна як групувати, так і відносити кожне спостереження до окремої групи. Остання умова відкриває можливість ефективного аналізу при малих вибірках.