2.Как работают слабо-, нормально- и переармированные сечения?
Еще раз отметим, что по условиям статики Nb = Ns, или RbAb = RsAs. Отсюда видно, что с увеличением Аs увеличивается и Аb, а значит, увеличивается и х. С помощью схем на рис. 29 рассмотрим, как деформируются бетон и арматура перед разрушением нормального сечения в зависимости от степени армирования.
В слабо армированном сечении (а), при х < хR, деформации в арматуре достигли начала площадки текучести (s = pl), а в бетоне не достигли предельной сжимаемости (b < bu). Казалось бы, прочность бетона здесь недоиспользуется, и сечение работает нерационально. Но на самом деле, у арматуры имеется резерв – площадка текучести, а это значит, что по мере текучести стали, когда деформации в ней увеличиваются с pl до pl1 (рис. 29,г), растут и деформации бетона, достигая в итоге bu (рис. 29,а, пунктирная линия). Если вместо “мягкой” стали установить “твердую”, не имеющую площадки текучести, то деформации в ней к моменту разрушения превысят величину 02, соответствующую условному пределу текучести 02, и составят 02.1 (рис. 29, г), что учитывается коэффициентом условий работы s6: чем меньше х, тем больше s6. Следовательно, в слабо армированном сечении напряжения в “мягкой” стали достигают предела текучести и реализуют Rs, в “твердой” стали превышают условный предел текучести и составляют Rss6; напряжения в бетоне тоже, в конце концов, достигают расчетного сопротивления Rb.
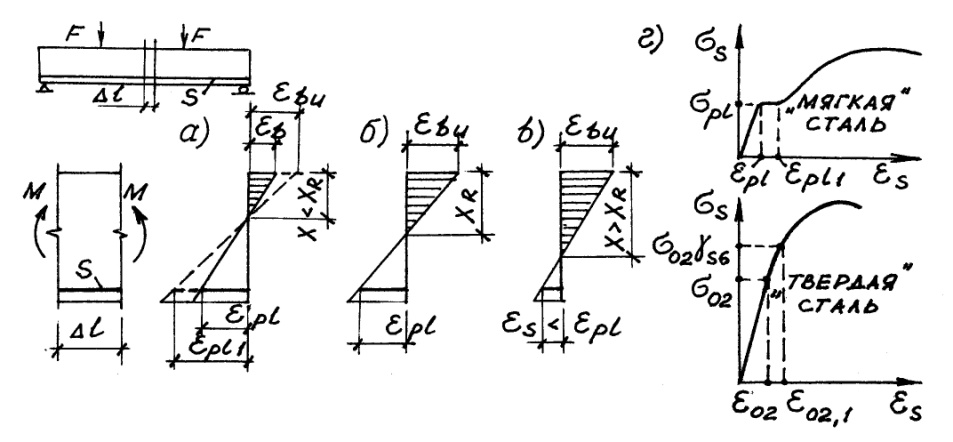
Рис. 29
Нормально армированное сечение при х = хR, работает наиболее рационально (б): b и s одновременно достигают значений соответственно bu и pl (или 02), а напряжения одновременно достигают значений соответственно Rb и Rs.
В переармированном сечении (в) при х > хR, деформации бетона достигают bu, а деформации арматуры не достигают pl (02), т.е. прочность бетона Rb используется полностью, а прочность арматуры Rs – частично: s < Rs. Причем, чем больше х, тем меньше s.
Слабо и нормально армированные сечения имеют один общий признак: бетон и арматура полностью используют свою прочность, поэтому принцип расчета у них одинаков (1-й случай расчета). Переармированные сечения рассчитывают иначе (2-й случай). Границей между случаями является величина хR (или R), поэтому ее и называют граничной высотой сжатой зоны.
4 Какие уравнения статики используют при расчете прочности наклонных сечений на поперечную силу?
Всего одно уравнение: Q = 0, отсюда и условие прочности: Q Qu = Qb + Qsw + Qs,inc (рис. 41), где Qsw = RswAsw = qswco поперечная сила, воспринимаемая поперечной арматурой (хомутами), или, говоря иначе, – несущая способность поперечной арматуры, пересекающей наклонную трещину; Qs,inc = RswAs,incsin поперечная сила, воспринимаемая отогнутой арматурой, или вертикальная проекция усилий в отогнутых стержнях, пересекающих наклонную трещину; Qb= b2 (1 + n+f) Rbtbho2/c = Mb /c поперечная сила, воспринимаемая бетоном сжатой зоны, или несущая способность бетона сжатой зоны на срез (растянутый бетон после образования наклонной трещины из работы выключен). |
В
Рис.41
выражении для Qb коэффициент b2 учитывает вид бетона (для тяжелого b2 = 2), n учитывает наличие внешней продольной силы (сжимающая сила например, сила предварительного обжатия повышает сопротивление бетона, тогда n > 1; растягивающая сила снижает, тогда n < 1); f учитывает наличие полки в сжатой зоне (свесы увеличивают сопро-тивление сжатой зоны, тогда f > 1). Значения n и f по отдельности и в сумме не должны превышать 0,5. В других выражениях Rsw расчетное сопротивление растяжению поперечной и отогнутой арматуры.Сложность задачи состоит в том, что в единственном уравнении статики содержатся два неизвестных: горизонтальная проекция наклонной трещины со и горизонтальная проекция расстояния от грани опоры до вершины наклонной трещины с (в Нормах она именуется проекцией наклонного сечения). Без них не найти ни Qb, ни Qsw, ни даже Q.
Заметим, что в научно-технической литературе величину с часто именуют «плечом среза», а Mb = Qbc – «моментом среза». Нельзя не признать, что эти термины более просты и понятны, чем принятые в Нормах.