1) Определить скорость падения камня, брошенного под углом к горизонту, по времени его полета. [условие и решение]

Если камень, брошенный под углом 30° к горизонту, находился в полете 2 с, то с какой скоростью он упал на землю?

Решение:

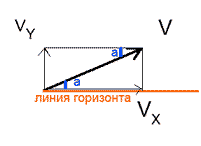Если камень был в полете 2 с, то в силу симметрии 1 с он летел до максимальной точки подъема и 1 с падал вниз (сопротивлением воздуха мы пренебрегаем). В максимальной точке подъема камень имеет только горизонтальную составляющую V_x скорости V. Свободно падая с максимальной высоты подъема, за 1 с камень приобретет вертикальную скорость V_y, равную:

V_y = gt

Скорость бросания равна скорости падения тела, которая связана с вертикальной составляющей в момент падения:

V =	vy	=	gt
	sin α		sin α

Искомая скорость равна V = 20 м/с.

Ответ: камень упал на землю со скоростью 20 м/с.

2) Тело бросили горизонтально с вершины наклонной плоскости. Через некоторое время оно ударилось о плоскость. Узнать начальную скорость. [условие и решение]

• задачи с решениями

• кинематика

• криволинейное движение

• механика

• равноускоренное движение

• свободное падение

С вершины наклонной плоскости, образующей с горизонтом угол 60°, бросают тело в горизонтальном направлении. Если через 3,5 с тело ударилось о плоскость, то с какой начальной скоростью оно было брошено?

Эта задача была размещена посетителями в разделе Решаем вместе 3 июня 2007 года.

Решение:

Высоту полета тела H определим по формуле:

H =	gt2	.
	2

Дальность полета по горизонтали S будет равна:

S = v_ot.

Отношение высоты полета тела H к дальности полета по горизонтали S равно:

gt2	•	1	= tg α.
2		vot

Находим v_o:

gt	= tg α.
2vo

gt	= tg α.
2vo

vo	=	gt	.
		2tg α

Если принять g = 10 м/с², то v_o = 10.1 м/с.

Ответ: начальная скорость тела равна 10.1 м/с.

3) С башни с начальной скоростью брошено горизонтально тело. Определить радиус кривизны траектории через определенное время. [условие и решение]

»

С башни брошено тело в горизонтальном направлении со скоростью 15 м/с. Пренебрегая сопротивлением воздуха, определить радиус кривизны траектории тела через 2 с после начала движения.

Решение:

Радиус кривизны траектории — это радиус окружности R, по которой в этот момент движется тело.

Через две секунды тело приобретет скорость v, в которой вертикальная составляющая равна v_y = gt:

v = √(vx2 + vy2) = √(vx2 + (gt)2).

(1)

Нормальное ускорение тела a_n:

an =	v2	,
	R

откуда радиус окружности R равен:

R =	v2	. (2)
	an

Нормальное ускорение a_n связано соотношением:

an = g•cos α,

где

cos α =	vx	,
	v

тогда:

an =	gvx	. (3)
	v

Подставляя (3) и (1) в (2), получим:

R =	vv2	=	√(vx2 + (gt)2)	• (vx2 + (gt)2).
	gvx		gvx

После вычислений R = 104,2 м.

Ответ: радиус кривизны через 2 с составляет 104,2 м.

Движение по окружности: задачи с решениями

1) Колесо вращалось равнозамедленно и за некоторое время уменьшило частоту вращения. Известен момент инерции колеса. Найти угловое ускорение колеса, тормозящий момент, работу сил торможения, число оборотов за это время. [условие и решение]

Колесо, вращаясь равнозамедленно, при торможении уменьшило за 1 минуту частоту вращения от 300 до 180 об/мин. Момент инерции колеса равен 2 кг•м². Найти: 1) угловое ускорение колеса; 2) тормозящий момент; 3) работу сил торможения; 4) число оборотов, сделанных колесом за эту минуту.

Решение:

При равнозамедленном вращении колеса имеем изменение угловой скорости:

Δw = w2 − w1 = 2πn2 − 2πn1 = 2π(n2 − n1).

Угловое ускорение равно отношению изменения угловой скорости ко времени

ε =	Δw	=	2π(n2 − n1)	.
	t		t

Момент торможения (тормозящий момент) будет равен:

M = Jε = J	2π(n2 − n1)	.
	t

Работа сил торможения равна изменению кинетической энергии:

−A = W2 − W1 =	Jw12	−	Jw12	=	J(2πn2)2	−	J(2πn1)2	= 2π2J(n22 − n12).
	2		2		2		2

То есть:

A = 2π2J(n12 − n22).

Наконец, число оборотов можно определить так (поскольку движение равнозамедленное):

N =	t(n1 + n2)	.
	2

Проведем расчеты: ε = −0.21 рад/с²; М = −0.42 Н•м; A = 631 Дж; N = 240 оборотов.